Mathematik 11/Rechnen mit Vektoren

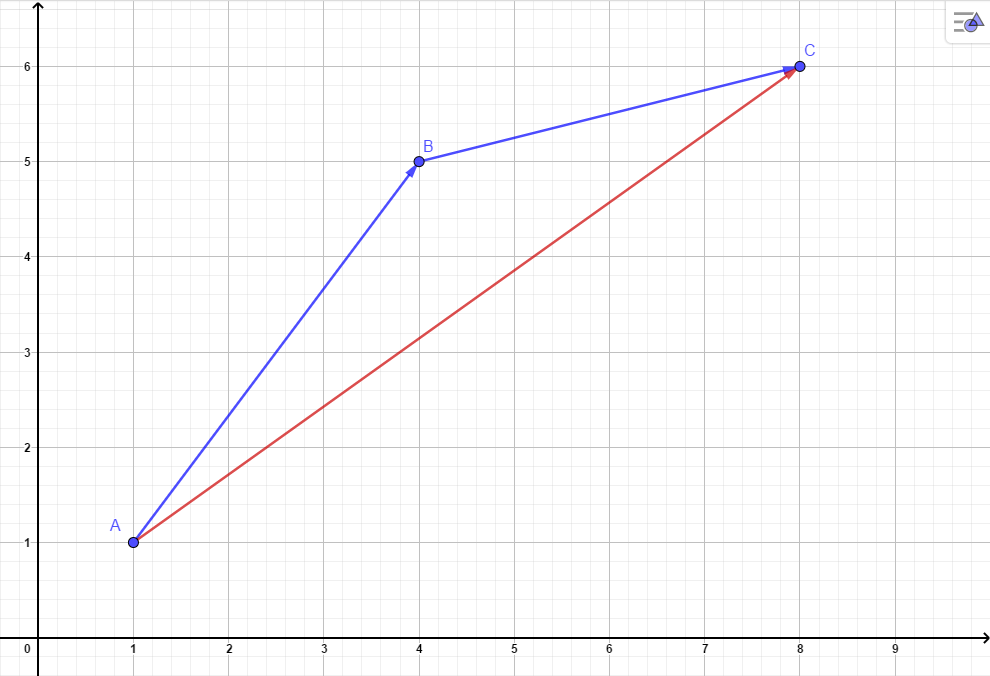
Arbeitsblatt zum Rechnen mit Vektoren

Führt man zwei Verschiebungen hintereinander aus, so ergibt sich wieder eine neue Verschiebung. In der Abbildung werden die Verschiebungen der Vektoren $\vec{AB} = \begin{pmatrix}3\\4\end{pmatrix}$ und $\vec{BC} = \begin{pmatrix}4\\1\end{pmatrix}$ hintereinander ausgeführt. Zum gleichen Endzustand gelangt man jedoch auch, wenn nur die Verschiebung des Vektors $\vec{AC}$ ausgeführt wird.

Aufgabe

• Geben Sie die Koordinaten des Vektors $\vec{AC}$ an.
• Stellen Sie eine Vermutung zur Beziehung zwischen dem Vektor $\vec{AC}$ und den Vektoren $\vec{AB}$ und $\vec{BC}$ auf. Notieren Sie Ihre Hypothese. Vergleichen Sie anschließend mit der Lösung.

Lösung anzeigen

$\vec{AC}=\begin{pmatrix}7\\5\end{pmatrix}=\begin{pmatrix}3\\4\end{pmatrix}+\begin{pmatrix}4\\1\end{pmatrix}=\vec{AB}+\vec{BC}$

Merke

Mersatz anzeigen

Sind zwei Vektoren $\vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$ gegeben, dann heißt $\vec{a}+\vec{b}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}+\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}=\begin{pmatrix}a_1+b_1\\a_2+b_2\\a_3+b_3\end{pmatrix}$ die Summe der Vektoren $a$ und $b$.

Bearbeite folgende

Übung zur Vektoraddition

Merke

Gegeben ist der Vektor $\vec{a}$. Der Vektor $-\vec{a}$ heißt Gegenvektor zu $\vec{a}$.

Aufgabe

Das nebenstehende Applet zeigt einen Vektor $\vec{b}$ und seinen Gegenvektor $-\vec{b}$.

• Verändern Sie den Anfangs- und Endpunkt des Vektors $\vec{b}$. Beobachten Sie dabei die Koordinaten des Gegenvektors.
• Welchen Vektor erhält man, wenn man den Vektor $\vec{b}$ und seinen Gegenvektor $-\vec{b}$ addiert?

Lösung anzeigen

Addiert man zum Vektor $\vec{b}$ den Gegenvektor $-\vec{b}$, so erhält man den Nullvektor: $\vec{b}+(-\vec{b})=\vec{b}-\vec{b}=\vec{0}$.

Merke

Der Vektor $\begin{pmatrix}0\\0\end{pmatrix}$ (bzw. $\begin{pmatrix}0\\0\\0\end{pmatrix}$) heißt Nullvektor und wird mit $\vec{0}$ bezeichnet.

Definition Vektoraddition

Vektorsubtraktion

Merke

Die Addition des Vektors $\vec{a}$ mit dem Gegenvektor von $\vec{b}$ entspricht der Subtraktion bzw. Differenz:

$\vec{a}+(-\vec{b})=\vec{a}-\vec{b}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}-\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}=\begin{pmatrix}a_1-b_1\\a_2-b_2\\a_3-b_3\end{pmatrix}$.

Aufgabe

• Ziehen Sie an den Vektoren $\vec{a}$ und $\vec{b}$. Beobachten Sie dabei die Koordinaten von $\vec{a}$, $\vec{b}$ und $\vec{c}$.
• Verschieben Sie die Spitze von $\vec{a}$ zur Spitze von $\vec{b}$. Welchen Vektor erhalten Sie?

Lösung anzeigen

Man erhält den Nullvektor $\vec{0}$

• Verschieben Sie die Spitze von $\vec{a}$ zur Spitze von $-\vec{b}$. Was fällt Ihnen auf?

Lösung anzeigen

Der Vektor $\vec{c}$ entspricht einer Verdoppelung des Vektors $\vec{a}$ bzw. des Vektors $-\vec{b}$

Zusatz:

• Weisen Sie durch Verschieben des Anfangspunktes von $\vec{a}$ nach, dass auch hier eine Hintereinanderausführung der Vektoren zum Ergebnis $\vec{c}$ führt.

Gegenvektor

Übungen

https://unterrichten.zum.de/wiki/WHG_Q1_Vektorrechnung/WHG_Q1_Kurze_Übungen_zur_Vektorsubtraktion

Sie sehen hier zwei Vektoren $\vec{a}$ und $\vec{b}$ sowie einen Schieberegler für ein sogenanntes "Skalar" $t$.

Aufgabe

• Verändern Sie den Wert des Skalars $t$ durch Ziehen am Schieberegler. Geben Sie mit Hilfe der Darstellung eine Rechenvorschrift für die skalare Multiplikation (auch Skalarmultiplikation genannt) eines Vektors mit einer Zahl an und notieren Sie diese.

Hilfe 1 anzeigen

Betrachten Sie zunächst Vektoren mit ganzzahligen Einträgen.

Hilfe 2 anzeigen

Finden Sie zunächst einen Zusammenhang zwischen den jeweils ersten Einträgen der Vektoren.

• Für welche Werte von $t$ haben beide Vektoren dieselbe Orientierung?

Lösung anzeigen

Für $t>0$ haben beide Vektoren dieselbe Orientierung.

• Für welchen Wert von $t$ wird $\vec{b}$ zum Gegenvektor von $\vec{a}$?

Lösung anzeigen

Für $t=-1$ wird $\vec{b}$ zum Gegenvektor von $\vec{a}$.

Informationen anzeigen

Ein Skalar ist eine mathematische Größe, die allein durch die Angabe eines Zahlenwertes vollständig beschrieben ist.

Zum Beispiel ist die Aussage „Wir treffen uns in einer Stunde“ völlig ausreichend, um den gewünschten Zeitpunkt durch eine Zahl und eine Einheit zu beschreiben.

Hingegen ist die Aussage „Wir treffen uns in 500 m Entfernung von hier“ nicht ausreichend, da eine Richtungsangabe fehlt.

Der Lernpfad wurde übernommen von https://unterrichten.zum.de/wiki/WHG_Q1_Vektorrechnung (An einigen Stellen überarbeitet)