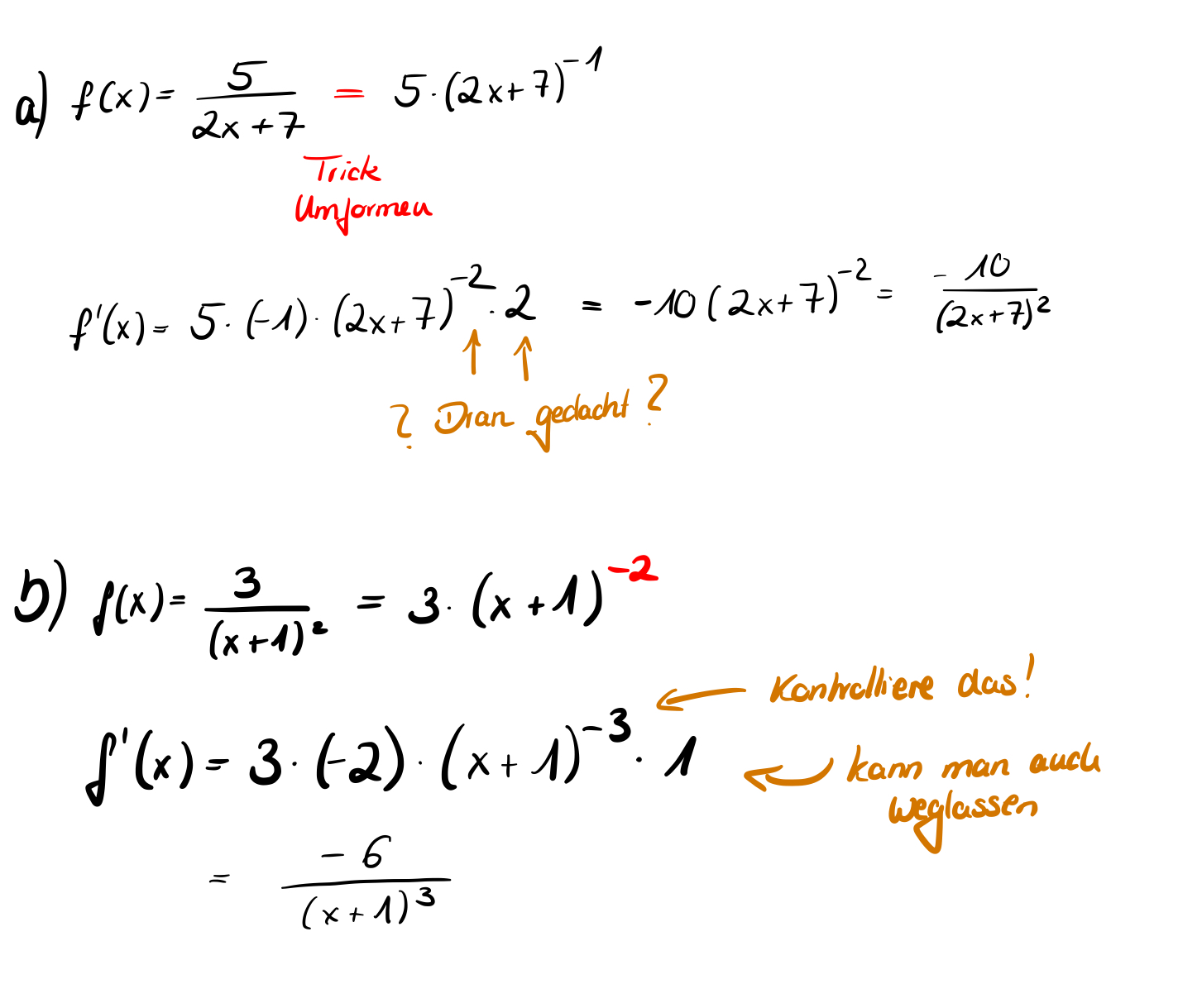Mathematik 11/Ableitung verketteter Funktionen: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 39: | Zeile 39: | ||
:a) <math>f(x)=\frac{5}{2x+7}</math> | :a) <math>f(x)=\frac{5}{2x+7}</math> | ||
:b) <math>f(x)=\frac{3}{(x+1)^{2}}</math> | :b) <math>f(x)=\frac{3}{(x+1)^{2}}</math> | ||
{{Lösung versteckt|1=. | {{Lösung versteckt|1=[[Datei:Beispiel Kettenregel 2.jpg]]|2=Aufdecken|3=Verbergen}} | ||
|3=Üben}} | |3=Üben}} | ||
Version vom 4. Februar 2021, 20:55 Uhr