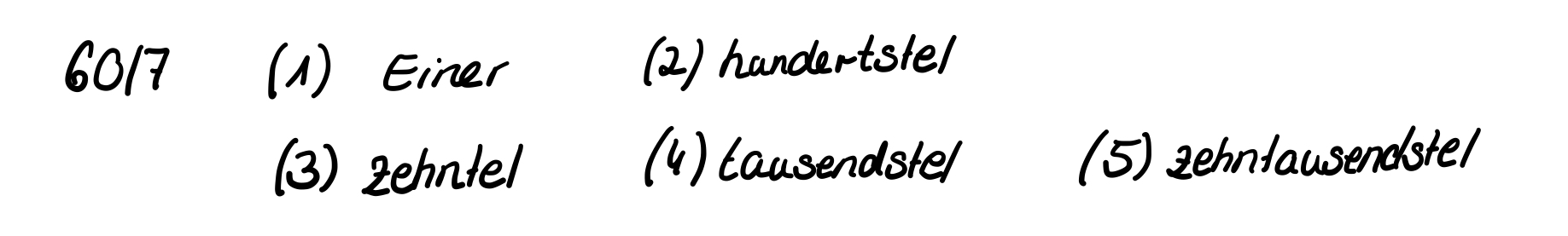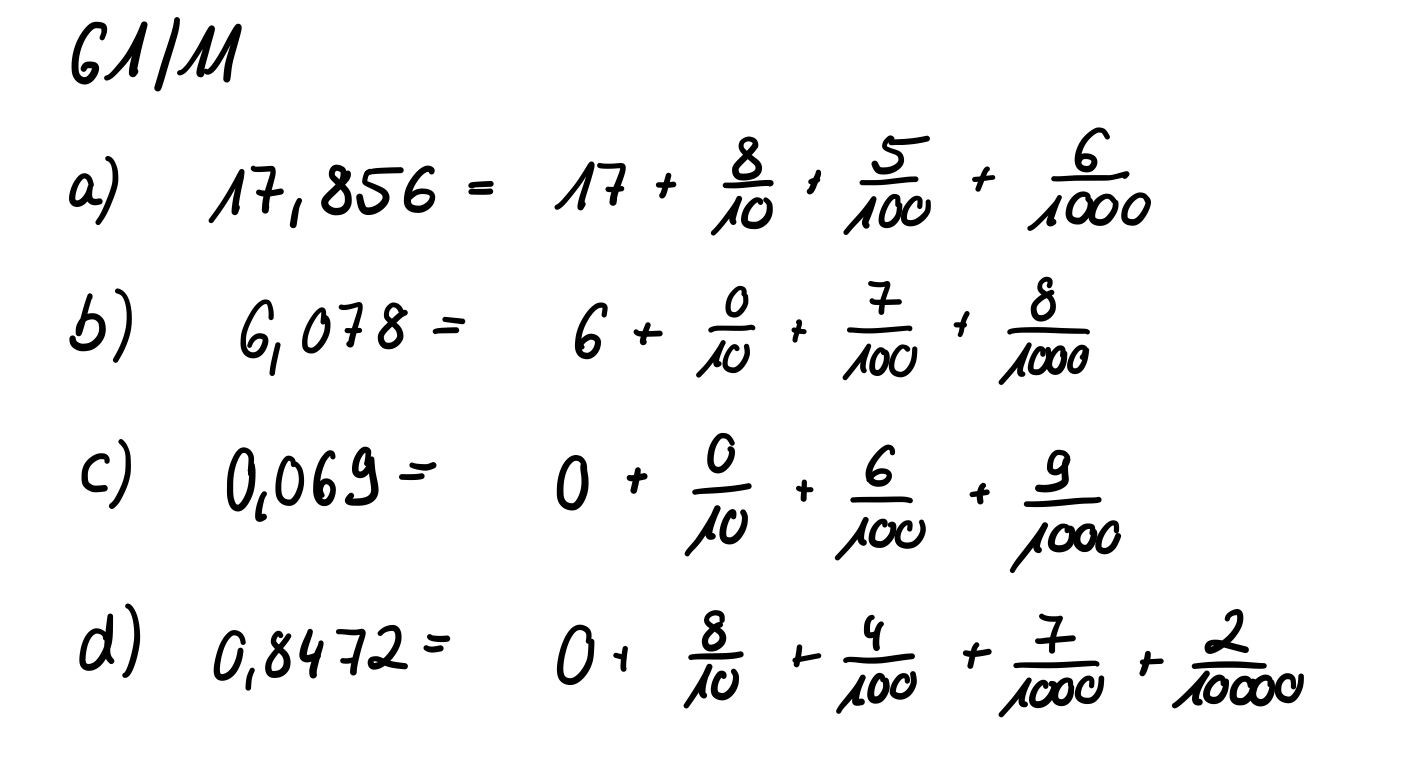6a 2020 21/Dezimalbrüche: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (28 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Teil 1== | |||
{{Box|Kommazahlen im Alltag| | {{Box|Kommazahlen im Alltag| | ||
Wo habt ihr im Alltag Kommazahlen entdeckt? <br> | Wo habt ihr im Alltag Kommazahlen entdeckt? <br> | ||
| Zeile 6: | Zeile 7: | ||
{{Box|Info| | {{Box|Info| | ||
{{#ev:youtube|zD6hXZGrumE|800|center}} | |||
|Kurzinfo}} | |Kurzinfo}} | ||
| Zeile 27: | Zeile 29: | ||
{{Box| Übung 3| | {{Box| Übung 3| | ||
Bearbeite die Übungen im '''Übungsheft''' | Bearbeite die Übungen im '''Übungsheft''' | ||
*S.60/7 | *S.60/7 | ||
*S.61/11 | *S.61/11 | ||
Vergleiche mit den Lösungen. | Vergleiche mit den Lösungen. | ||
{{Lösung versteckt| | |||
[[Datei:60 7.jpg|60 7.jpg]] | |||
|Lösung S.60/7 anzeigen|Lösung verbergen}} | |||
{{Lösung versteckt| | |||
[[Datei:61 11.jpg|61 11.jpg]] | |||
|Lösung S.61/11 anzeigen|Lösung verbergen}} | |||
|Üben }} | |||
{{Box|1=Info|2= | |||
<math>4,13 = 4 +\frac{1}{10} +\frac{3}{100}</math><br> | |||
Hier kann man ein Zehntel erweitern:<br> | |||
<math>= 4 +\frac{10}{100} +\frac{3}{100}</math><br> | |||
das ergibt dann:<br> | |||
<math>= 4 +\frac{13}{100} </math><br> | |||
also:<br> | |||
<math>4,13 = 4\frac{13}{100}</math> | |||
|3=Kurzinfo}} | |||
{{Box| Übung 4| | |||
Bearbeite die Übungen im '''Übungsheft''' | |||
*S.60/6a | |||
Vergleiche mit den Lösungen. | |||
{{Lösung versteckt| | |||
[[Datei:60 6a.jpg|60 6a.jpg]] | |||
|Lösung S.60/6a anzeigen|Lösung verbergen}} | |||
|Üben }} | |||
==Teil 2== | |||
{{Box|Warm Up| | |||
Gestern haben wir Dezimalzahlen in Brüche verwandelt. Heute drehen wir dies um. Wir wandeln Brüche in Dezimalbrüche um.<br> | |||
Bearbeite im Buch S.61/13 und verbessere die Übung. | |||
{{Lösung versteckt| | |||
a) 0,2 - 0,19 - 0,04 - 0,049 - 0,0026 - 0,0003 <br> | |||
b) 2,007 - 5,25 - 7,85 - 10,04 | |||
|Lösung S.61/13 anzeigen|Lösung verbergen}} | |||
|Üben}} | |||
{{Box|1=Info|2= | |||
Schreibe nun folgende zwei Dezimalbrüche als Brüche und vergleiche sie.<br> | |||
a) 0,7 und 0,70<br> | |||
b) 2,1 und 2,100 | |||
{{Lösung versteckt|1= | |||
<math> 0,7=\frac{7}{10} </math> und <math>0,70=\frac{70}{100} </math><br> | |||
<math> 2,1=2\frac{1}{10}</math> und <math>2,100=2\frac{100}{1000} </math><br> | |||
Kürzt man den zweiten Bruch, erhält man den ersten:<br> | |||
<math>0,70=\frac{70}{100}=\frac{7}{10}=0,7 </math><br> | |||
<math>2,100=2\frac{100}{1000} = 2\frac{1}{10} = 2,1</math><br> | |||
Da 0,70=0,7 und 2,100=2,1 kann man also die Nullen am Ende weglassen. | |||
|2=Lösung|3=Lösung verbergen}} | |||
|3=Kurzinfo}} | |||
{{Box|1=Merke|2= | |||
Schreibe ins Merkheft | |||
{{Lösung versteckt|1= | |||
Wenn man bei einem Dezimalbruch Endnullen anhängt oder weglässt, dann bleibt der Wert unverändert . <br> | |||
0,7 = 0,70 = 0,700 = 0,7000 usw. | |||
|2=Hefteintrag anzeigen|3=Hefteintrag verbergen}} | |||
|3= Merksatz}} | |||
{{Box|Überflüssige Nullen| | |||
Welche Nullen kann man bei jeder Zahl weglassen, ohne dass sich der Wert des Dezimalbruches ändert? | |||
a) 2,50 b) 2,05 c) 2,0500 d) 00,500 e) 02,505 | |||
{{Lösung versteckt|Zahlen ohne die gestrichenen Nullen. <br> | |||
a) 2,5: Endnullen können weggelassen werden<br> | |||
b) 2,05: Die Null in der Mitte muss bleiben!<br> | |||
c) 2,05: Endnullen können weggelassen werden<br> | |||
d) 0,5: eine Null vor dem Komma reicht. <br> | |||
e) 2,505: Führende Nullen können weggelassen werden <br> | |||
Keine Nullen in der Mitte streichen! | |||
|Lösung|Verbergen}} | |||
|Üben}} | |||
{{Box|Anton| | |||
Bearbeite in Anton den Pin "Dezimalzahlen kennenlernen" | |||
|Üben}} | |||
==Teil 3== | |||
{{Box|1=Info|2= | |||
Du weißt, dass <math>1% = \frac{1}{100}</math> <br> | |||
und du weißt, dass <math>\frac{1}{100}=0,01</math> <br> | |||
also folgt , dass 1% = 0,01 | |||
|3=Kurzinfo}} | |||
{{Box|Übung 1| | |||
{{LearningApp|app=pc3zrycxt20|width=100%|height=500px}} | |||
|Üben}} | |||
{{Box|1=Erinnerung|2= | |||
Bisher haben wir nur Brüche mit dem Nenner 10, 100, 1000... in Dezimalbrüche umgewandelt. Wir möchten jedoch auch Brüche umwandeln, die andere Nenner haben. | |||
|3=Meinung}} | |||
{{Box|1=Umformen durch Erweitern/Kürzen auf Stufenzahlen|2= | |||
Wie gehst du vor, um einen Bruch in einen Dezimalbruch umzuwandeln? <br> | |||
Hast du schon eine Idee? <br> | |||
Fülle den Lückentext aus. | |||
<div class="lueckentext-quiz"> | |||
Um einen '''Bruch''' in einen '''Dezimalbruch''' umzuwandeln, müssen wir den Bruch auf den '''Nenner''' 10, 100, 1000 … '''erweitern bzw. kürzen'''. | |||
</div> | |||
|3=Unterrichtsidee}} | |||
{{Box|1=Merke|2= | |||
Schreibe in dein Merkheft. | |||
{{Lösung versteckt| | |||
Um einen Bruch in einen Dezimalbruch umzuwandeln, müssen wir den Bruch auf den Nenner 10, 100, 1000... erweitern und dann umwandeln. <br> | |||
Das geht jedoch nicht mit jedem Bruch. | |||
|Hefteintrag anzeigen|Hefteintrag verbergen}} | |||
|3= Merksatz | |||
}} | |||
{{Box|Übung 2| | |||
Wandle in den Apps jeweils die Brüche in Dezimalbrüche um. Falls nötig, erweitere bzw. kürze. | |||
{{LearningApp|app=pk0qofww320|width=100%|height=1300px}} | |||
{{LearningApp|app=pnibmmy6t20|width=100%|height=800px}} | |||
|Üben }} | |||
{{Box|Übung 3| | |||
Übe in Anton. Bearbeite die Übungen beim Pin "Brüche und Dezimalzahlen". | |||
Das Teilkapitel "Umwandeln durch Division" ist freiwillig. Der Rest ist Pflicht. | |||
|Üben }} | |Üben }} | ||
'''ENDE''' | |||
Aktuelle Version vom 23. November 2020, 15:12 Uhr
Teil 1
Teil 2
Teil 3
ENDE