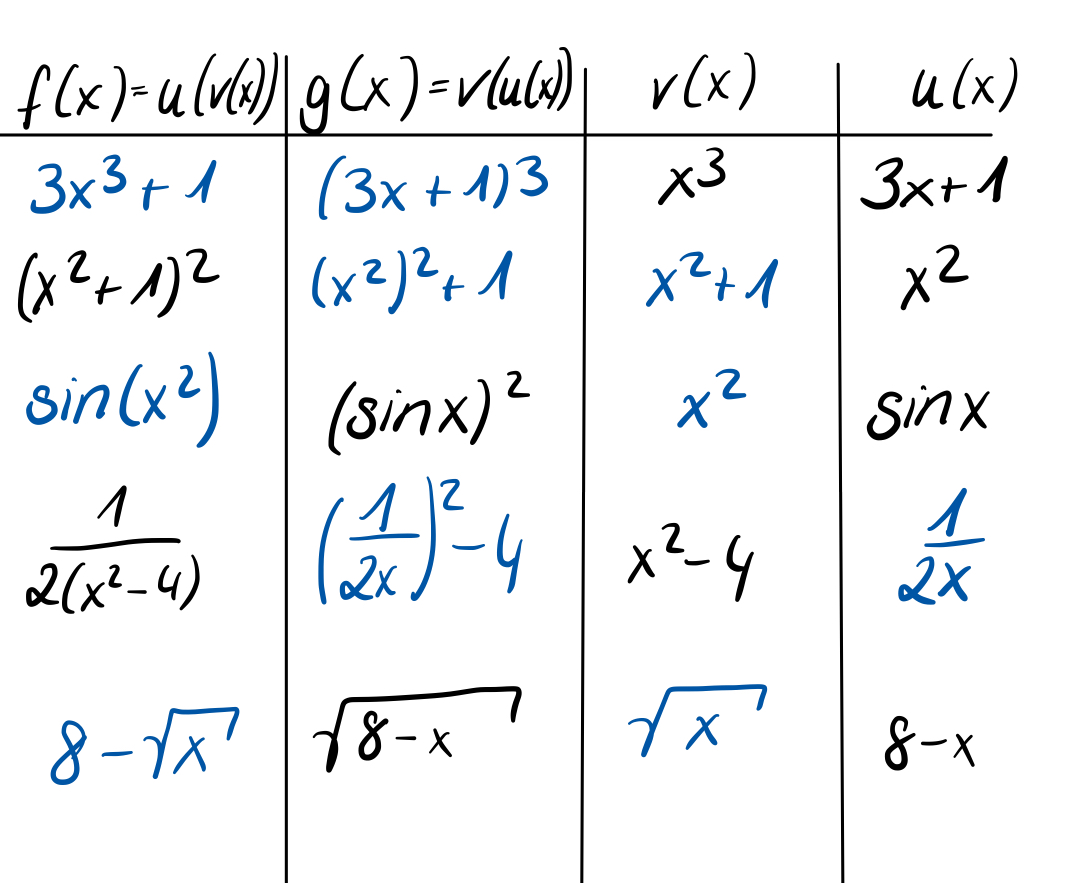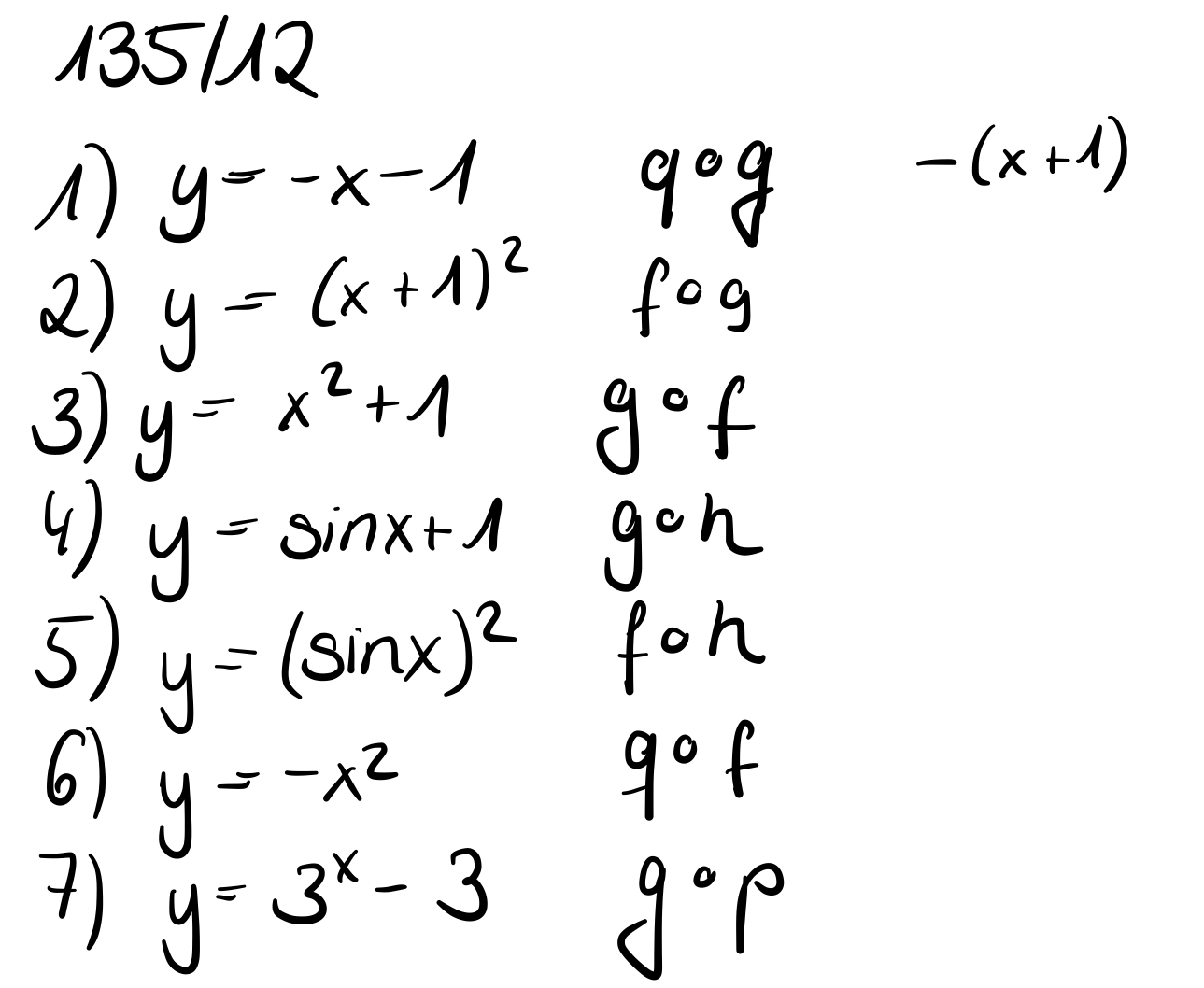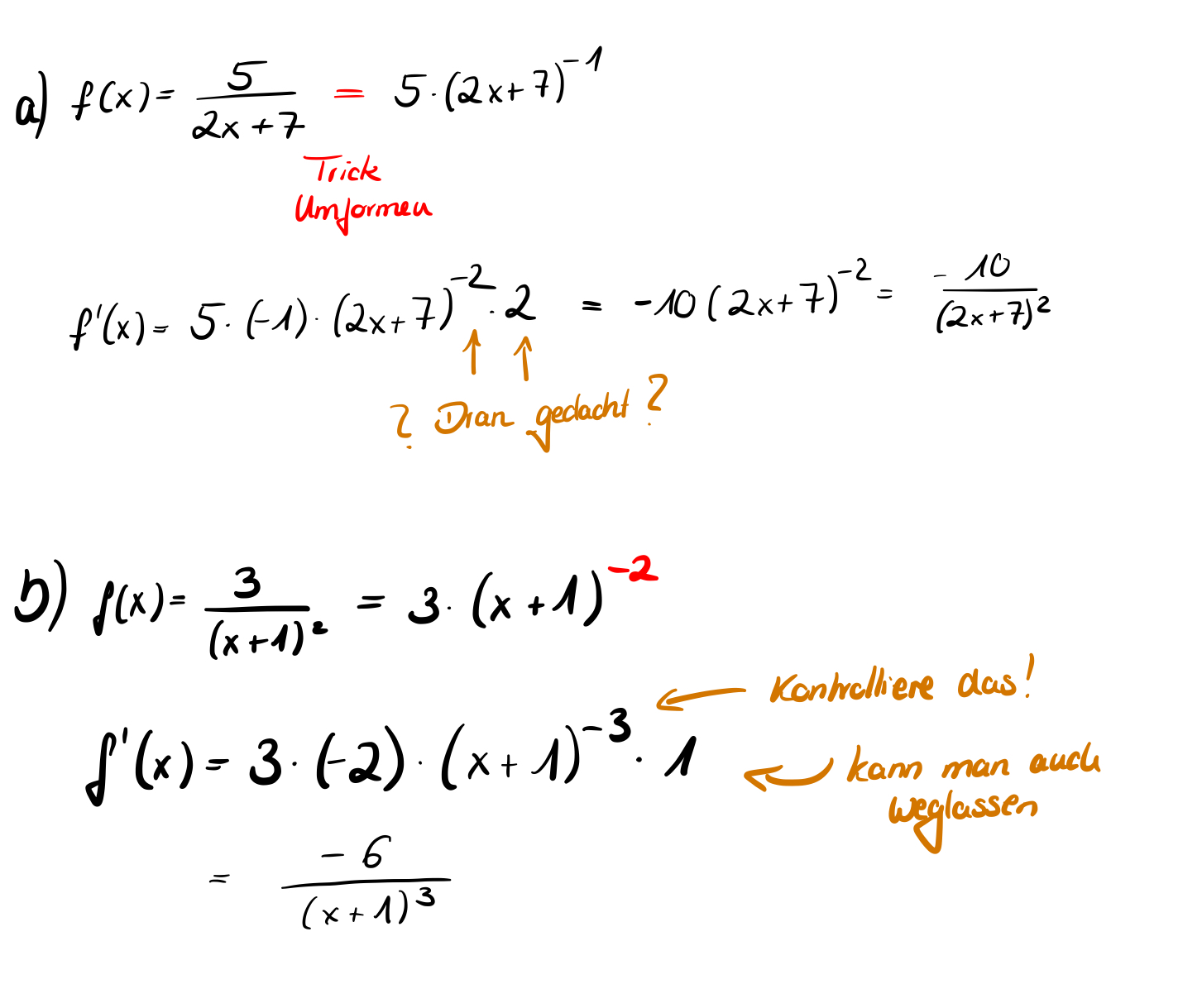Mathematik 11/Ableitung verketteter Funktionen: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (13 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box|1=Video|2=Schau dir das Video an. Halte an und notiere die Beispiele. Gehe zurück, wenn dir etwas zu schnell geht und wiederhole es. {{#ev:youtube| | {{Box|1=Video: Verkettete Funktionen|2=Schau dir das Video an. Halte an und notiere die Beispiele. Gehe zurück, wenn dir etwas zu schnell geht und wiederhole es. {{#ev:youtube|5Zrl5_-KbBk|600|center}} | ||
|3=Hervorhebung1}} | |||
{{Box|1=Üben|2= | {{Box|1=Üben|2= | ||
Bearbeite S.134/4a- | Bearbeite S.134/4a-e<br> | ||
{{Lösung versteckt|1=.. | {{Lösung versteckt|1=[[Datei:134-4.jpg|134-4.jpg|600|center]]|2=Aufdecken|3=Verbergen}} <br> | ||
Gute Übung für Fortgeschrittene S.135/12 | Gute Übung für Fortgeschrittene S.135/12 | ||
{{Lösung versteckt|1=.. | {{Lösung versteckt|1=[[Datei:135-12.jpg|135-12.jpg|600|center]]|2=Aufdecken|3=Verbergen}} | ||
|3=Üben}} | |3=Üben}} | ||
{{Box|1=Video|2={{#ev:youtube| | {{Box|1=Video: Ableitung verketteter Funktionen|2={{#ev:youtube|RdaEW05CCxA|600|center}}|3=Hervorhebung1}} | ||
{{Box|1=Merke|2=<math>u(v(x))=u'(v(x)) \cdot v'(x) | |||
</math> | |||
# Äußere Funktion ableiten und dabei | |||
# Innere Funktion beibehalten | |||
# Innere Funktion nachdifferenzieren|3=Merksatz}} | |||
{{Box|1=Video: Noch ein gemeinsames Beispiel|2=<br> | |||
{{#ev:youtube|MjQFoQfcg1c|600|center}}|3=Hervorhebung1}} | |||
{{Box|1=Üben|2= | {{Box|1=Üben|2= | ||
Bilde die Ableitung zu folgenden Funktionen <br> | Bilde die Ableitung zu folgenden Funktionen <br> | ||
:a) <math>f(x)=(x^ | :a) <math>f(x)=(x^3-4)^{5}</math> | ||
:b) <math>f(x)=frac{1}{3}(4-3x)^{3}</math> | :b) <math>f(x)=\frac{1}{3}(4-3x)^{3}</math> | ||
:c) <math>f(x)=(4x+5)^{-2}</math> | :c) <math>f(x)=(4x+5)^{-2}</math> | ||
:d) <math>f(x)=x^{2}+(2x+1)^{4}</math> | :d) <math>f(x)=x^{2}+(2x+1)^{4}</math> | ||
{{Lösung versteckt|1=. | {{Lösung versteckt|1=[[Datei:Lösung Übung Kettenregel.png]]|2=Aufdecken|3=Verbergen}} | ||
|3=Üben}} | |3=Üben}} | ||
{{Box|1=Video: Kettenregel bei gebrochen-rationalen Funtionen|2=<br> | |||
{{#ev:youtube|JGEfIDev7k8|600|center}}<br> | |||
ACHTUNG ACHTUNG: Im Video ist ein x verloren gegangen. Hier ist ein Bild mit dem x: | |||
[[Datei:VerlorenesX.jpg|500px|left]]|3=Hervorhebung1}} | |||
{{Box|1=Üben|2= | {{Box|1=Üben|2= | ||
Bilde die Ableitung zu folgenden Funktionen mit der Kettenregel. Überprüfe, ob du das Ergebnis mit der Quotientenregel bestätigen kannst. | Bilde die Ableitung zu folgenden Funktionen mit der Kettenregel. Überprüfe, ob du das Ergebnis mit der Quotientenregel bestätigen kannst. | ||
:a) <math>f(x)=5 | :a) <math>f(x)=\frac{5}{2x+7}</math> | ||
:b) <math>f(x)=3 | :b) <math>f(x)=\frac{3}{(x+1)^{2}}</math> | ||
{{Lösung versteckt|1=. | {{Lösung versteckt|1=[[Datei:Beispiel Kettenregel 2.jpg]]|2=Aufdecken|3=Verbergen}} | ||
|3=Üben}} | |3=Üben}} | ||
{{Box|1=Hausaufgabe|2= | |||
*S.137/2a,b,d,i,k | |||
*S.137/5 außer g | |||
*S.137/7a,b,c,d | |||
|3=Arbeitsmethode}} | |||
Aktuelle Version vom 5. Februar 2021, 08:00 Uhr