Benutzer:Thomas Lux: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(AA B7 begonnen) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 4: | Zeile 4: | ||
[[https://rmgwiki.zum.de/wiki/10d_2019_20/Chemie]] | [[https://rmgwiki.zum.de/wiki/10d_2019_20/Chemie]] | ||
==Arbeitsauftrag | ==Arbeitsauftrag Biologie7 (verpflichtend)== | ||
*Die folgende verpflichtende Unterrichtseinheit hat eine Bearbeitungszeit von ca. | *Die folgende verpflichtende Unterrichtseinheit hat eine Bearbeitungszeit von ca. 30 Minuten. | ||
*Ihr benötigt für die Bearbeitung: Das Schulbuch, einen Zettel, Stift und Ruhe. | *Ihr benötigt für die Bearbeitung: Das Schulbuch, einen Zettel, Stift und Ruhe. | ||
*Bitte bearbeitet die gestellten Aufgaben tatsächlich erst selbst, bevor ihr auf | *Bitte bearbeitet die gestellten Aufgaben tatsächlich erst selbst, bevor ihr auf "Lösung" klickt! | ||
{{Box-spezial | {{Box-spezial | ||
|Titel=<span style="color:#080">''' | |Titel=<span style="color:#080">'''Ziel'''</span> | ||
|Inhalt= | |Inhalt= | ||
Langfristig möchte ich mit euch den Begriff "ökologische Nische" klären. In dieser Einheit wird das aber noch nicht geschehen. Um diesen Begriff zu verdeutlichen, werde ich bestimmten Grafiken arbeiten. Grafiken, die etwas komplizierter sind, als ihr gewohnt seid.<br> | |||
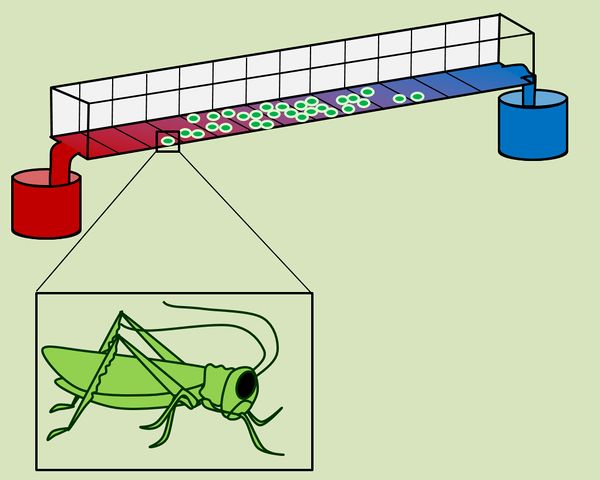
Eine Grafik, die so ähnlich auch in eurem Buch auf der S. 71 enthalten ist, seht ihr hier: <br> | |||
[[Datei:A6_TempOrgel_Heuschrecke.jpg|600px]]<br> | |||
| | |||
|Farbe= #080 | |Farbe= #080 | ||
|Rahmen= 0 | |Rahmen= 0 | ||
| Zeile 27: | Zeile 24: | ||
{{Box-spezial | {{Box-spezial | ||
|Titel=<span style="color:#080">''' | |Titel=<span style="color:#080">'''Wiederholung'''</span> | ||
|Inhalt= | |Inhalt= | ||
Normalerweise beginnt ihr beim Interpretieren einer Grafik zunächst mit einer bestimmten Floskel: "Die Grafik zeigt... in Abhängigkeit von...". Das funktioniert bei der oberen Grafik nicht! Zur Wiederholung noch einmal anhand einer einfacheren Grafik. Wendet die Floskel an: | |||
[[Datei:A6_TempOrgel_Heuschrecke.jpg|600px]]<br> | [[Datei:A6_TempOrgel_Heuschrecke.jpg|600px]]<br> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
* | * Die Grafik zeigt die Wachstumsrate von Mehlwürmern in Abhängigkeit von der Temperatur. | ||
* Man erkennt eine typische Optimuskurve mit einer optimalen Wachstumsrate bei ca. 30%... | |||
* usw... | |||
|Lösung | |Lösung|Lösung ausblenden}} | ||
|Farbe= #080 | |Farbe= #080 | ||
|Rahmen= 0 | |Rahmen= 0 | ||
| Zeile 48: | Zeile 43: | ||
{{Box-spezial | {{Box-spezial | ||
|Titel= | |Titel=<span style="color:#080">'''Zerlegung der Grafik in Komponenten'''</span> | ||
|Inhalt= | |Inhalt= | ||
Die | Die Floskel kann auf die eingangs gezeigte Grafik nicht angewendet werden, weil hier DREI Parameter dargestellt sind, während die Grafik von den Mehlwürmern nur ZWEI Parameter enthält. <br> | ||
* | * Mehlwurmkurve: Temperatur, Wachstumsrate | ||
[[Datei: | * Kiefernspinner: Temperatur, Luftfeuchtigkeit, Schlüpferfolg | ||
Normalerweise braucht man für jeden Parameter eine eigene Achse. Im Bild vom Kiefernspinner ist die dritte Achse einfach weggelassen, bzw. kommt sie auf euch zu! Das folgende Bild zeigt, wie man sich die Grafik dreidimensional auch vorstellen könnte: | |||
[[Datei:A6_TempOrgel_Heuschrecke.jpg|600px]]<br> | |||
<br> | <br> | ||
Vielleicht kennt ihr solche Darstellungen aus eurem Atlas: Auch da werden Berge mit "Höhenlinien" dargestellt. Man kann aus der aufgeschlagenen Seite eines Atlas ja kein Gebirge herauswachsen lassen.<br> | |||
Mit dieser Darstellung solltet ihr jetzt auch etwas besser die Floskel anwenden können: Das was in einer zweidimensionalen Grafik die '''y-Achse''' ist, ist hier die '''z-Achse'''. Und das was in einer zweidimensionalen Grafik die '''x-Achse''' ist, ist hier die '''x- und die y-Achse'''. Versucht es jetzt mit der Floskel! | |||
{{Lösung versteckt| | |||
Die Grafik zeigt den Schlüpferfolg von Kieferspannern in Abhängigkeit von der Temperatur und der Luftfeuchtigkeit.<br> | |||
Wenn ihr das hinbekommen habt: TOLL! :) | |||
|Lösung|Lösung ausblenden}} | |||
|Lösung | |||
|Farbe= #080 | |Farbe= #080 | ||
|Rahmen= 0 | |Rahmen= 0 | ||
| Zeile 69: | Zeile 69: | ||
|Titel= | |Titel= | ||
|Inhalt= | |Inhalt= | ||
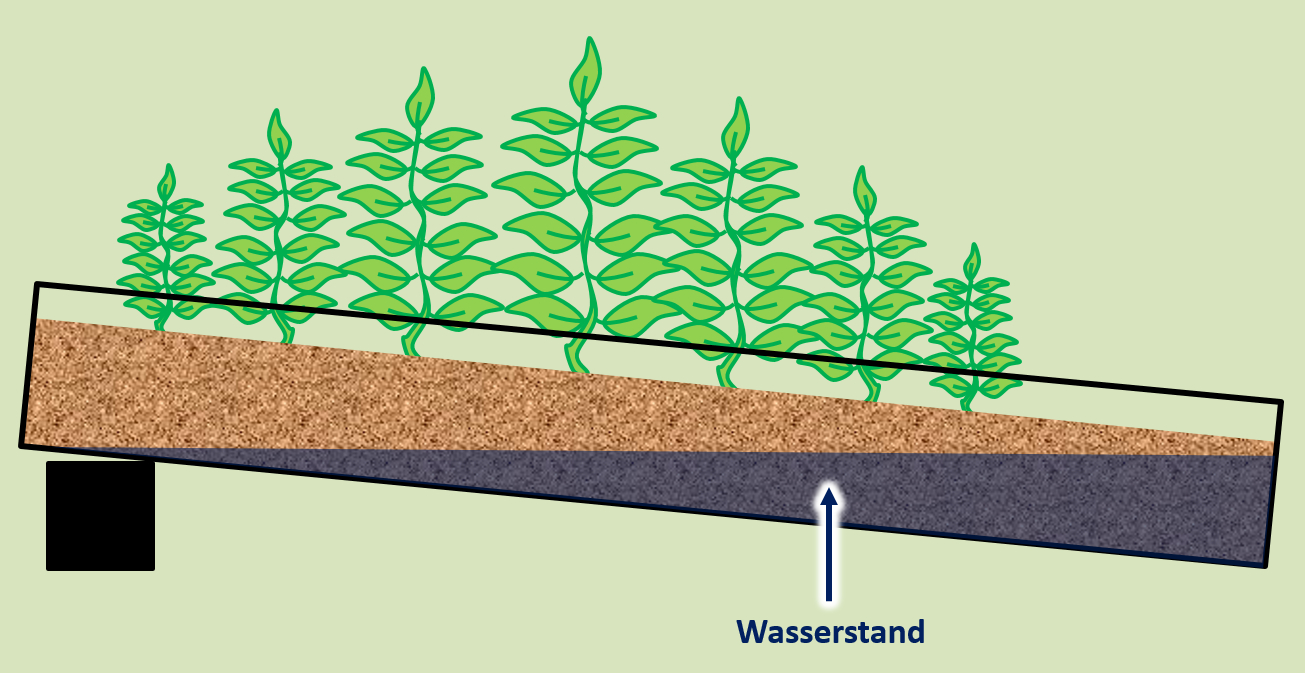
Man kann aus dieser dreidimensionalen Darstellung auch wieder zweidimensionale Grafiken machen, indem man einen Paramater einfach konstant lässt. Zum Beispiel: Man kann den Schlüpferfolg von Kieferspannern in Abhängigkeit von der Luftfeuchtigkeit in eine Grafik zeichnen. Die Temperatur soll in allen Fällen immer gleich 20°C bleiben. Versucht diese Grafik zu zeichnen. Dazu ist in der folgenden dreidimensionalen Abbildung eine Hilfslinie hervorgehoben (die rote 20°C-Linie):<br> | |||
<br> | <br> | ||
* Zeichnet | |||
* Zeichnet zunächst ein Achsensystem (y-Achse: Schlüpferfolg, x-Achse: Luftfeuchtigkeit) | |||
* Fahrt dann mit eurem Finger die rote Linie auf dem Diagramm hier am Bildschirm entlang und übertragt die Werte, bei denen sich euer Finger gerade befindet in die passende Stelle eures gezeichneten Koordinatenkreuzes. | |||
{{Lösung versteckt| | {{Lösung versteckt| | ||
[[Datei:A6_WasserverfügbarkeitsOrgel.jpg]]<br> | |||
[[Datei: | Die geschrichelte Linie ist eine "geglättete" Linie. Die ist etwas realistischer<br> | ||
<br> | |Lösung|Lösung ausblenden}} | ||
|Lösung | |||
|Farbe= #080 | |Farbe= #080 | ||
|Rahmen= 0 | |Rahmen= 0 | ||
| Zeile 92: | Zeile 87: | ||
{{Box-spezial | {{Box-spezial | ||
|Titel= | |Titel= | ||
|Inhalt= | |Inhalt= | ||
Das Ganze geht natürlich auch mit dem anderen Parameter: Leitet aus dem dreidimenionalen Diagramm ein zweidimensionales Ab | |||
{{Lösung versteckt| | {{Lösung versteckt| | ||
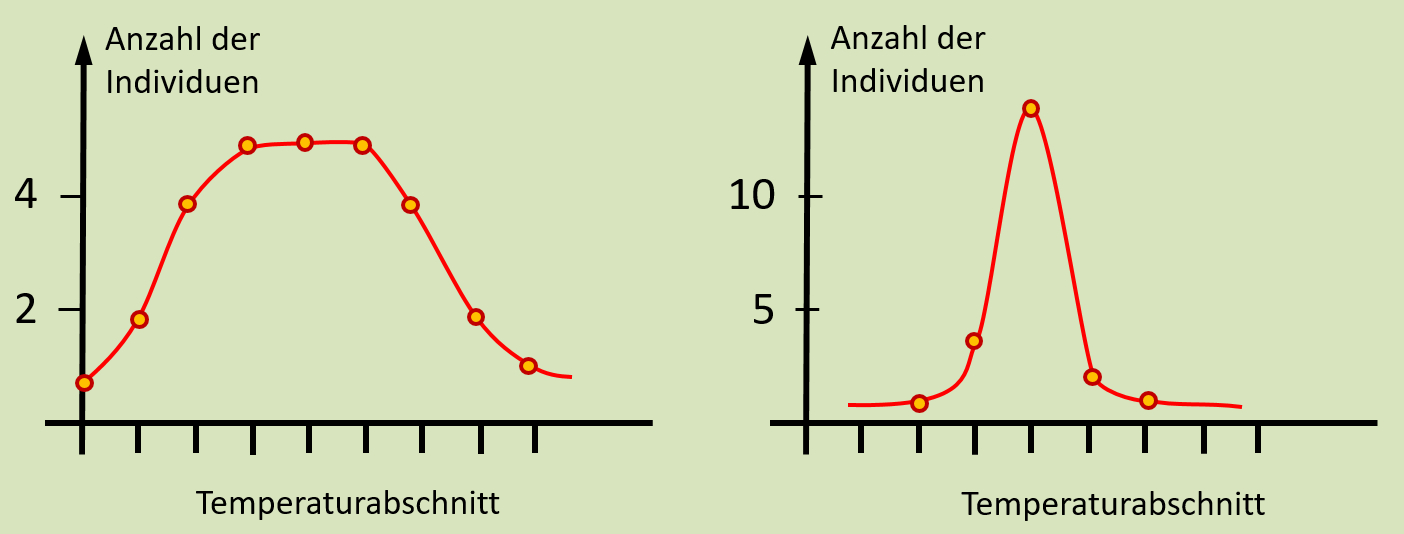
* | [[Datei:A6_TempOrgel_Vergleich_Grafik.jpg]]<br> | ||
<br> | |||
|Lösung | * Bei der Grafik von den Ameisen halten sich nahezu alle im selben Temperaturbereich auf. Es gibt nur wenige Abweichler und die sind immer noch dicht bei den anderen. Lebewesen, die auf einen sehr engen Bereich bezüglich eines Umweltfaktors begrenzt sind, nennt man '''Spezialisten''', oder als Adjektiv: Sie sind '''stenök '''(wenn sie bezüglich vieler Faktoren Spezialisten sind) oder '''steno...''' wenn es nur um einen Faktor geht (hier also '''stenotherm''', weil sie Spezialisten bezüglich des Faktors Temperatur sind) | ||
* Bei der Grafik von den Heuschrecken erkennt man, dass sich die Heuschrecken über einen viel größeren Bereich verteilen. Tiere, die Umweltfaktoren in großen Schwankungen tolerieren nennt man '''Generalisten '''oder als Adjektiv: Sie sind '''euryök '''(wenn sie bezüglich vieler Faktoren Generalisten sind) oder '''eury...''' wenn es nur um einen Faktor geht (hier also '''eurytherm''', weil sie Generalisten bezüglich des Faktors Temperatur sind) | |||
|Lösung |Lösung ausblenden}} | |||
|Farbe= #080 | |Farbe= #080 | ||
|Rahmen= 0 | |Rahmen= 0 | ||
Version vom 27. April 2020, 17:24 Uhr
Hallo! Meine Benutzer-Seite ist eine Art Steinbruch, in der hauptsächlich für mich wichtige Vorlagen liegen und einige Tests laufen...
[[1]]
Arbeitsauftrag Biologie7 (verpflichtend)
- Die folgende verpflichtende Unterrichtseinheit hat eine Bearbeitungszeit von ca. 30 Minuten.
- Ihr benötigt für die Bearbeitung: Das Schulbuch, einen Zettel, Stift und Ruhe.
- Bitte bearbeitet die gestellten Aufgaben tatsächlich erst selbst, bevor ihr auf "Lösung" klickt!
Arbeitsauftrag Chemie5 (verpflichtend)
- Die folgende verpflichtende Unterrichtseinheit hat eine Bearbeitungszeit von ca. 45 Minuten.
- Ihr benötigt für die Bearbeitung: Das Schulbuch, das PSE, einen Zettel, Stift und Ruhe.
- Bitte bearbeitet die gestellten Aufgaben tatsächlich erst selbst, bevor ihr auf die Lösung klickt!
Testseiten
Eiweiß-Test-Seite
H5P-Test-Seite
Q11-Struktur-Test-Seite
verlinkte Seiten
Zu den Arbeitsaufträgen in Bio (Corona)
Zu den Arbeitsaufträgen Chemie (Corona)
Zur Schulentwicklungs-Testseite
Zur Studien- und Berufsorientierung
Zur Studien- und Berufsorientierung der Mittelstufe
Biologie-Rätsel des Monats
Biologie
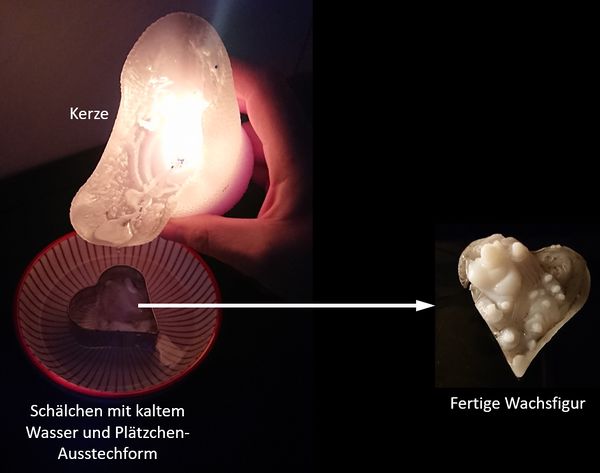
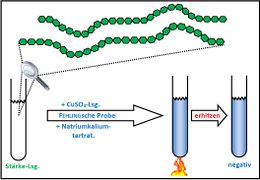
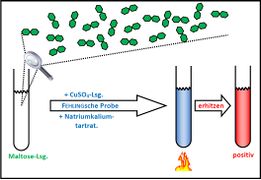
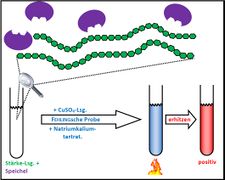
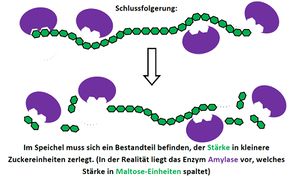
Visualisierung der Unterrichtsversuche zum Thema "Verdauungsprozesse im Mund".
Chemie
Das Anfertigen eines Versuchsprotokolls stellt eine wichtige Grundfertigkeit dar. Auch im Hinblick auf das spätere Erstellen einer Seminararbeit. In den naturwissenschaftlichen Fächern ist die typische Gliederung einer Arbeit nämlich einem Versuchsprotokoll ganz ähnlich. Hier zwei gelungene Beispiele: