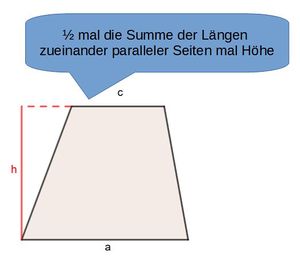
M6 4.3 Flächeninhalt eines Trapezes

<6b 2020 21| Mathe 6B

Mittwoch, den 3.3.2021

In der Mathematik versucht man oft, Formeln/REchnungen auf schon bekanntest zurückzuführen. Das galt bei der Berechnung des Flächeninhaltes für Paralelogramme und auch für Dreiecke. Das gleiche versucht man auch für das Trapez.

Wie berechnet man den Flächeninhalt eiens Trapezes und wieso?

Sieh dir das Video mindestens zweimal an!
https://edpuzzle.com/media/603ce54ce3e33342a7ab8302

Übung 1

Bearbeite S.144/2.
Notiere wie folgt:
a) $A=\frac{1}{2}\cdot (a+c)\cdot h=\frac{1}{2}\cdot (3+8)\cdot 3=16,5$
Trage deine Lösung ein und überprüfe die Lösung.

b) A= 15()
c) A= 14()
d) A= 65,6()

Falls du nicht den richtigen Flächeninhalt berechnet hast, überprüfe deine Maße für a, c und h in den folgenden Lücken.

b) (a + c) = 10()
h = 3()

c) (a + c) = 7()
h = 4()

b) (a + c) = 16,4()
h = 8() (ohne ,0)

Merksätze

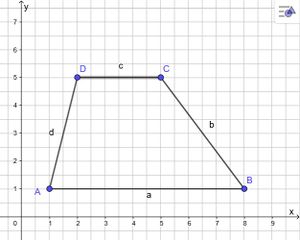
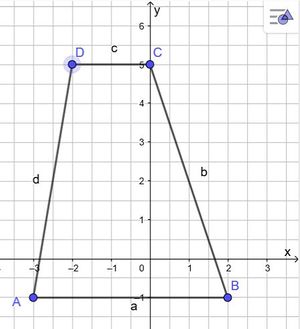
Trage die folgenden Merksätze in dein Merkheft! Bitte zeichnet die Trapeze selber!

4.3 Flächeninhalt von Trapezen

Den Abstand zweier zueinander paralleler Grundseiten eines Trapezes nennt man Höhe.

Für den Flächeninhalt A eines Trapezes mit den Längen a und c der zueinander parallelen Seiten und der zugehörigen Höhe h gilt:

$A=\frac{1}{2}\cdot (a+c)\cdot h$
 

Beispiel: a = 8 cm; c = 3 cm; h = 3 cm

$A=\frac{1}{2}\cdot (a+c)\cdot h=\frac{1}{2}\cdot (3cm+8cm)\cdot 3cm=16,5c{m}^2$

Flächeninhalt von Trapezen berechnen

Berechne mindestens 2 Trapeze!

Nun sollst du Trapeze zeichnen und berechnen.

S. 144/4a,c (wie beim Dreieck, sollst du ohne messen, die Höhe und dei Seitenlängen ablesen)

a= 7cm; c = 3 cm; h = 4 cm
$A=\frac{1}{2}\cdot (a+c)\cdot h=\frac{1}{2}\cdot (7cm+3cm)\cdot 4cm=\frac{1}{2}\cdot 10cm\cdot 4cm=5cm\cdot 4cm=20c{m}^2$

Kontrolliere jeden Punkt, wenn du nicht das gleiche Ergebnis hast. Welchen Fehler hast du gemacht?

a= 5cm; c = 2 cm; h = 6 cm
$A=\frac{1}{2}\cdot (a+c)\cdot h=\frac{1}{2}\cdot (5cm+2cm)\cdot 6cm=\frac{1}{2}\cdot 7cm\cdot 6cm=42c{m}^2:2=21c{m}^2$

Kontrolliere jeden Punkt, wenn du nicht das gleiche Ergebnis hast. Welchen Fehler hast du gemacht?

Textaufgabe

S. 144/6

Gegeben: a = 100 cm; c = 60 cm; h = 70 cm

$A=\frac{1}{2}\cdot (a+c)\cdot h=\frac{1}{2}\cdot (100cm+60cm)\cdot 70cm=5600c{m}^2$

A= 5600cm² = 56 dm² = 0,56 m² Kosten: 35€ pro m²

Kosten:0,56 m² * 35 € = 19,60 €

Übungen zu den Brüchen

S.126 /11d Denke an eine fortlaufende Rechnung. Ich habe 6 Zeilen benötigt.

Lösung der Aufgaben: S.126/11: Hier nur die Lösungen, wenn du Fehler hast und sie nicht findest, dann schicke mir deine Lösung. Prüfe erst, ob du vollständig gekürzt hast.

d)$2\frac{27}{32}$

ABGABEN überprüfen!

Bitte überprüft, ob ihr eine Nachricht von mir erhalten habt, dass noch Abgaben fehlen. Holt diese heute alle dringend nach.

• Wochenplan 13 (17.2.)
• Arbeitsblatt zum Lernpfad Parallelogramm (24.2.)
• Merkhefteinträge zum Dreieck und Parallelogramm (Do. 25.2.)

Die meisten kann ich nur loben, da sie alle Aufträge pünktlich abgeben. Für euch gilt diese Nachricht nicht!

Freitag, den 5.03.2021

Spickzettel

Schreibe dir eine Spickzettel zu den Flächeninhalten. Er soll folgendes enthalten.

• Zeichne ein Quadrat, Rechteck, Parallelogramm, Trapez und Dreieck.
• Beschrifte diese.
• Notiere die Formel für Flächeninhalt A= und den Umfang U= neben das jeweilige Vier-/Dreieck.
• Größe: DIN A5 oder A4
• Lade den Spickzettel im Modul Lernen hoch.

Übungen Flächeninhalten

S.146 /1a Mache ein Skizze in dein Heft, um deinen Lösungsweg besser darzustellen.

Der Maßstab ist gegeben:
1:50 000 heißt 1cm in der Zeichnung sind 50 000cm in Wirklichkeit.

Miss in der Abbildung die Längen nach und rechne sie um.

Nur die zum Berechnen der Flächeninhalte benötigten Strecken. Vorsicht, ihr habt möglicherweise andere Strecken gewählt oder diese in einer Skizze anders beschriftet.

Parallelogramm ABEF
Strecke von A nach F gemessen: 2,2 cm
in Wirklichkeit: $\overline{AF}=2,2\cdot 50000cm=110000cm=1100m$

Höhe des Parallelogramms ABEF: gemessen: 0,8 cm in Wirklichkeit: $h_{ABEF}=0,8\cdot 50000cm=40000cm=400m$

Dreieck CDB
Strecke von C nach D gemessen: 3 cm
in Wirklichkeit: $\overline{CD}=3\cdot 50000cm=150000cm=1500m$

Höhe des Dreiecks CDB zur Ecke B: gemessen: 1,3 cm in Wirklichkeit: $h_{CDB}=1,3\cdot 50000cm=65000cm=650m$

Dreieck BDE
Strecke von D nach E gemessen: 1,4 cm
in Wirklichkeit: $\overline{DE}=1,4\cdot 50000cm=70000cm=700m$

Höhe des Dreiecks BDE zur Ecke B: gemessen: 2,2 cm

in Wirklichkeit: $h_{BDE}=2,2\cdot 50000cm=110000cm=1100m$

Übungen Flächeninhalten

S.146 /2a

A= 3,69m² + 28,8m² = 32,49m²

Abgabe

Gib die beiden Aufgaben S.146/1a und 2a im Modul Lernen ab. Du kannst auch Fragen dazuschreiben, wenn du nicht weiterkommst.

Übungen zu den Brüchen

S.126 /11e Denke an eine fortlaufende Rechnung. Ich habe 5 Zeilen benötigt.

Lösung der Aufgaben: S.126/11: Hier nur die Lösungen, wenn du Fehler hast und sie nicht findest, dann schicke mir deine Lösung. Prüfe erst, ob du vollständig gekürzt hast. Hast du an Punkt vor Strich gedacht?

d)$6\frac{8}{15}$