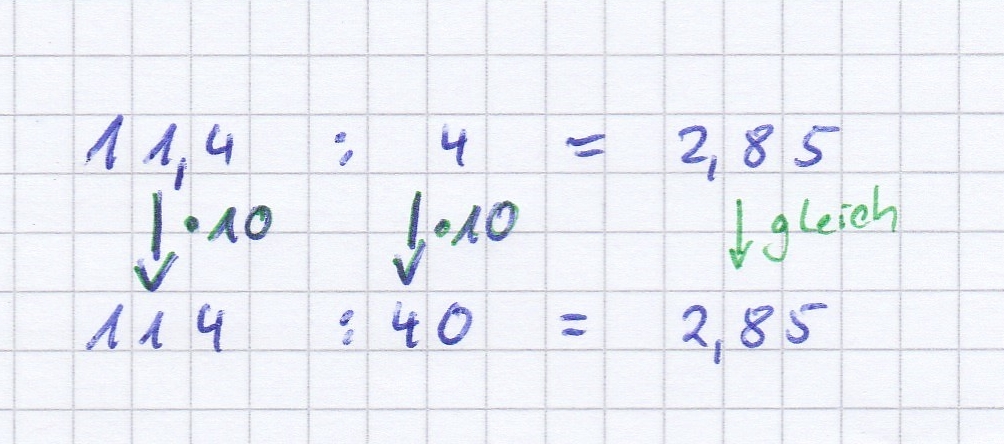M6 3.6 Dividieren von Dezimalzahlen
Mittwoch, 10.2. 2021
Eine blecherne Stimme weckt euch aus euren Gedanken! Wie lange sitzt ih rnun schon in diesem Klassenzimmer. Frau Licht wurde seit Donnerstag nicht mehr dazugeschaltet und vom Androiden ist keine Spur.
Ihr sortiert die Begriffe wieder an die richtige Stelle. Ein Kinderspiel, oder?
Ordne die Fachbegriffe richtig zu:
Addition: 1.Summand + 2.Summand = Wert der Summe
Subtraktion: Minuend - Subtrahend = Wert der Differenz
Mulitplikation: 1.Faktor * 2. Faktor = Wert des Produkts
Division: Dividend: Divisor = Wert des Quotienten
Du notierst ersteinmal die Rechnungen des Puzzle. Dann versuchst du es zu lösen und erinnerst dich an die vielen Umkehraufgaben, die du schon bewältigt hast.
Frau Licht hatte doch immer einen Tipp parat. Wenn man die Aufgaben mit einfachen Aufgaben lösen kann, dann muss man nur die anderen Zahlen einsetzen und lösen.
8: x= 2 --> x = 8:2 = 4
Hoffentlich hast du dich nicht verrechnet. Du zählst die Nachkommastellen aller Lösungen und kommst auf 5, wenn du alle unnötigen Nullen am Ende nach dem Komma weglässt.
Danach schreibst du zum Spaß alle 8 Ziffern der drei Lösung ohne das Komma hintereinander. Neugiereig blickst du dich wieder um. Bestimmt gibt es irgendwo wieder eine Möglichkeit diesen Code einzugeben. Du findest ein Display, bei dem du aber nur Buchstaben eingeben kannst. Du drehst und wendest deine Zahlen und entdeckst etwas außergewöhnliches. Vielleicht musst du auch etwas kreativ sein, aber ja. Das ist doch ein Unterrichtsfach, oder?
Du versuchst das Wort nur mir Großbuchstaben einzutippen.
_ _ _ _ _ _ _ _ 6 b
Du kommst nach 2 Versuchen immernoch nicht rein. Dann schreibe doch Frau Licht, vielleicht kann sie dir weiter oder du bist einfach noch nicht sicher in der Division mit Dezimalzahlen. Dann bearbeite S.115/10g-j und S.115/17.
Ihr möchtet aus dem Bioraum raus. Gerechnet habt ihr doch genug, oder? Ihr fragt eure Eltern nach der Lösung, um euch selber zu überprüfen. Welche Fehler habe ich gemacht? Verstehe ich sie?
Die Tafel vor dir verändert sich. Die Kreide ist weg und es erscheinen Matheaufgaben.
Freitag, 5.2. 2021
Um alle Rechenarten auch für Dezimalbrüche zu können, müssen wir nicht nur durch natürliche Zahlen teilen können.
Dafür habt ihr gestern eine wichtige Übung gemacht.
Vielleicht ist euch bei den Aufgaben etwa aufgefallen.
a) 11,4 : 4 = 2,85
b) 114 : 40 = 2,85
c) 6,09 : 7 = 0,87
d) 60,9 : 70= 0,87
Immer zwei Aufgaben haben das gleiche Ergebnis.
Ja, dass gilt immer und wird bei der Division durch Dezimalzahlen angewendet.
In der ersten Zeile siehst du eine Aufgabe, die du eigentlich noch garnicht lösen könntest. Aber die zweite Zeile hast du schon gelöst.
Du brauchst das Merkheft, einen Schmierzettel und einen bunten Stift.
Mache die Übungen und Überlegungen auf einem Schmierzettel.
Schreibe ALLE Beispiele ins Merkheft. Großer Danke an Frau Hetterich, die das Video mit Fragen gefüllt hat.
Notiere den Merksatz im Merkheft.
Dividieren durch einen Dezimalbruch
Man verschiebt bei beiden Zahlen das Komma um gleich viele Stellen nach rechts, bis der Divisor eine natürliche Zahl ist.
Dann dividiert man durch die natürliche Zahl.
Hier kommen ein paar Kopfrechenübungen.
1,2 : 0,4 = 3()
3,2 : 0,8 = 4()
3,2 : 0,08 = 40()
72 : 0,09 = 800()
0,56: 0,7 = 0,8()
1,44: 0,12 = 12()
Wie ändert sich das Ergebnis einer Division, wenn man nur den Divisor oder nur den Dividenden mit einer Stufenzahl (10,100,100) multipliziert oder dividiert?
Überlege, ob du S.114/7a mit nur einer Rechnung und nachdenken lösen kannst.Bearbeite nun S.114/7a.
Leider haben bisher nur sehr wenige Schüler die Aufgaben in Anton bearbeitet. Es bietet schnelle Rückmeldung bei Fehlern.
Schaue bitte nochmal, ob du alle Aufgaben diese Woche erledigt hast. Auch der Wochenplan 12 muss von einigen noch abgegeben werden. Danach geht es an den Wochenplan 13.
Hier nochmal die Aufgaben zum Prüfen, ob euer Heft vollständig ist:
- S.105/7a,e,f
- S.107/16 a, c
- S.107/20 a-c
- S.107/21
- S.110/4 (15min)
- S.110/5 i,j,k,l
- S.114/7a
- S.114/8a-c,e,j
Donnerstag, 4.2.2021
Notiere folgenden Merksatzeintrag in dein Heft:
3.6 Dividieren von Dezimalzahlen
Beim Dividieren von Dezimalbrüchen geht man so vor:
- Man dividiert wie bei natürlichen Zahlen.
- Beim Überschreiten des Kommas im Dividenden setzt man ein Komma im Ergebnis.
- Beim Ende der Rechnung muss man gegebenenfalls beim Dezmalbruch nicht geschriebene Endnullen ergänzen.
Stelle dir einen Timer auf 15min.
Bearbeite nun möglichst viele Aufgaben von S.110/4.
Lade folgende Aufgaben im Modul Lernen hoch, damit ich sehen kann, ob du es verstanden hast.
Zur Multiplikation von Dezimalbrüchen:
- S. 106/19 a-d
- S. 106/12 (Textaufgabe)
Zur Division von Dezimalzahlen mit natürlichen Zahlen
Berechne.
a) 11,4 : 4
b) 114 : 40
c) 6,09 : 7
