6e Lernen zu Hause: Umfang und Flächeninhalt eines Dreiecks

01.03.2021

WICHTIG:

Bitte noch nicht weiter auf dieser Seite lesen, wir treffen uns erst in der Videokonferenz, um uns über die Lösung zu S.142/ 18 auszutauschen und eventuelle Fragen zu Flächeninhalt eines Parallelogramms und auch eines Dreiecks zu klären...Hier werden wir auch gemeinsam Aufgaben lösen. Den Link zur Videokonferenz erhältst du rechtzeitig um Schulmanager - Modul Lernen.
Hier geht es für dich erst nach der Konferenz weiter!

Zur Wiederholung: Flächeninhalt Dreieck:

EmbedVideo fehlt ein anzugebender Parameter.

Zum Einstieg:

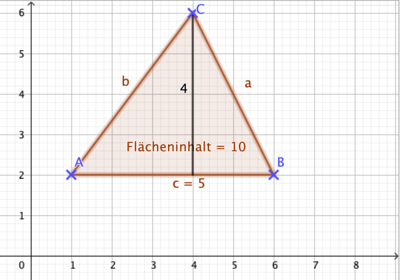
Hier kannst du testen, ob du die Berechnung des Flächeninhalts eines Dreiecks verstanden hast. Für mindestens drei Dreiecke solltest du dies heute noch testen!
Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite - z.B. indem du "F5" auf der Tastatur drückst, dann sollte es normalerweise klappen...

Übung:

Bearbeite B. S. 137/ 14 a) und d)!
Vergiss nicht die Anwendungsmöglichkeit einer Umkehrrechnung...

Lösung der Aufgaben:

a)

g = 3,2 cm und h = 1,9 cm
$A = \frac {1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 3,2 cm \cdot 1,9 cm = \frac{1}{2} \cdot (3,2 cm \cdot 1,9 cm) = \frac{1}{2} \cdot 6,08 cm^2 = 3,04 cm^2$

NR:
$32 \cdot 19 = 608$, da die beiden Faktoren zusammen zwei Nachkommastellen haben, ist das Ergebnis für den doppelten Flächeninhalt des Dreiecks 6,08 cm².
Vergiss bitte nicht "$cm \cdot cm = cm^2$"!
Um den Flächeninhalt des Dreiecks zu erhalten, muss man 6,08 cm² noch mit $\frac {1}{2}$ multiplizieren bzw. durch 2 dividieren und erhält somit als Ergebnis 3,04 cm²

d)
g = 127 m und A = 3175 m²

1. Möglichkeit:

$A = \frac{1}{2} \cdot g \cdot h$

Einsetzen liefert: $3175 m^2 = \frac{1}{2} \cdot 127 m \cdot h$

Zunächst berechnet man $\frac {1}{2} \cdot 127 m$ und erhält somit: $3175 m^2 = 63,5 m \cdot h$

Mit der Umkehraufgabe berechnet man h: $h= 3175 m^2 \div 63,5 m = 31750 m^2 \div 635 m = 50 m$

  2. Möglichkeit:

Verdopple zunächst den Flächeninhalt A des Dreiecks: $2 \cdot A = 2 \cdot 3175 m = 6350 m$

Löse mit der Umkehraufgabe - man teilt den doppelten Flächeninhalt der Dreiecksfläche durch die Grundseite und erhält somit die zugehörige Höhe:

$h = (2 \cdot A) \div g = 6350 m^2 \div 127 m = 50 m$
Vergiss bitte nicht "$m^2 \div m = m$"! Das Ergebnis muss eine Länge sein!

Nun der ultimative Test zum Abschluss:

Erkennst du alle Notationamöglichkeiten für den Flächeninhalt von Rechteck, Parallelogramm und Dreieck? Viel Erfolg!

03.03.2021

Info:

Heute übst du weiterhin Aufgaben zum Flächeninhalt eines Dreiecks... Der Umfang eines Dreiecks wird heute auch auftauchen, aber keine Angst, das wird nicht problematisch...
WICHTIG: Verbessere immer gewissenhaft deine Lösung mit meiner Lösung, falls du dennoch ein Feedback zu deiner Lösung haben möchtest oder eine Frage hast, schicke mir bitte eine Nachricht via Schulmanager oder stelle deine Frage morgen in der Videosprechstunde. Danke!
Den Link zur Videosprechstunde erhältst du rechtzeitig morgen via Schulmanager - Modul Lernen.

Zur Wiederholung:

Sei dir zunächst zu 100 % sicher, dass du die Formel zur Berechnung des Flächeninhalts eines Dreiecks weißt. Falls du dir nicht ganz sicher bist, lies bitte im Heft nach, bevor du mit den Aufgaben startest. Danke!

Übung - Dreiecke im Koordinatensystem (Teil 1):

Verwende zur Berechnung des Flächeninhalts die Grundseite mit ihrer zugehörigen Höhe, die sich problemfrei eindeutig im Koordinatensystem ablesen lässt!

Übung - Dreiecke im Koordinatensystem (Teil 2):

Bei folgender Aufgabe wirst du Dreiecke ins Koordinatensystem zeichnen, spitze bitte deinen Bleistift. Danke! Schau dir jeweils immer erst die Koordinaten an und überlege, wie groß das Koordinatensystem sein sollte.
Falls zum Einzeichnen von Koordinaten noch etwas unklar sein sollte, vorletzte Stunde gab es zur Wiederholung ein Video dazu, das kannst du gegebenfalls nochmal anschauen...Aber ich denke, es sollte alles klar sein.
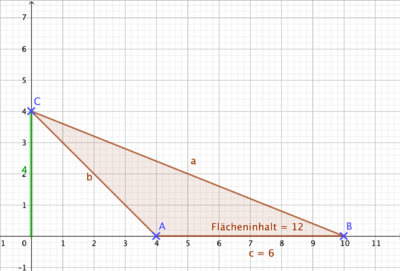
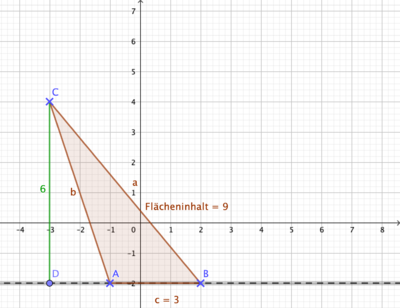
Bearbeite nun B. S. 136/8a), c), d)!

$A = \frac{1}{2} \cdot c \cdot h_c = \frac {1}{2} \cdot (5 cm \cdot 4 cm) = \frac{1}{2} \cdot 20 cm^2 = 10 cm^2$

$A = \frac{1}{2} \cdot c \cdot h_c = \frac {1}{2} \cdot (6 cm \cdot 4 cm) = \frac{1}{2} \cdot 24 cm^2 = 12 cm^2$

$A = \frac{1}{2} \cdot c \cdot h_c = \frac {1}{2} \cdot (3 cm \cdot 6 cm) = \frac{1}{2} \cdot 18 cm^2 = 9 cm^2$

Übung:

Bearbeite B. S. 135/ 3 und beschreibe mündlich - also vermutlich in Gedanken, was dir auffällt!
Notiere dir die Verallgemeinerung dieser Erkenntnis aus meiner Lösung bitte bei dieser Aufgabe in dein Heft. Danke!

Lösung der Aufgabe:

Berechnung des Flächeninhalts:
$A = \frac{1}{2} \cdot g \cdot h = \frac {1}{2} \cdot (2,3 cm \cdot 2 cm) = \frac{1}{2} \cdot 4,6 cm^2 = 2,3 cm^2$

Feststellung: Eigentlich muss man den Flächeninhalt des Dreiecks nur einmal berechnen, denn alle Dreiecke haben die gleiche Grundseite, 2,3 m lang, und die gleiche zugehörige Höhe, 2 cm lang.

Verallgemeinerung:

Dreiecke mit gleich langen Seiten und gleicher zugehöriger Höhe besitzen denselben Flächeninhalt.

Übung:

Bearbeite B. S. 136/ 9 a)! Welches Dreieck ist deiner Meinung nach größer bzw. kleiner? Schätze bevor du rechnest!
Anmerkung: 1 Kästchenlänge $\hat{=}$ 0,5 cm!

Lösung der Aufgabe:

Berechnung des Flächeninhalts - linkes Dreieck:
$A = \frac{1}{2} \cdot g \cdot h = \frac {1}{2} \cdot 2,5 cm \cdot 1,5 cm = 1,25 cm \cdot 1,5 cm = 1,875 cm^2$
Anmerkung:
In einer Nebenrechnung berechnet man $125 \cdot 15$, das Ergebnis ist hier 1875. Das Ergebnis für den Flächeninhalt des linken Dreiecks ist somit 1,875 cm², denn die Zahlen 1,25 und 1,5 haben gemeinsam drei Nachkommastellen.

Berechnung des Flächeninhalts - rechtes Dreieck:
$A = \frac{1}{2} \cdot g \cdot h = \frac {1}{2} \cdot 1,5 cm \cdot 2,5 cm = 0,75 cm \cdot 2,5 cm = 1,875 cm^2$
Anmerkung:
In einer Nebenrechnung berechnet man $75 \cdot 25$, das Ergebnis ist hier 1875. Das Ergebnis für den Flächeninhalt des rechten Dreiecks ist somit 1,875 cm², denn die Zahlen 0,75 und 2,5 haben gemeinsam drei Nachkommastellen.

Feststellung:
Die Länge der Grundseite des linken Dreiecks ist so lang wie die Höhe des rechten Dreiecks und die Grundseite des rechten Dreiecks ist so lang wie die Höhe des linken Dreiecks im Endeffekt berechnet man bei beiden Dreiecken für den Flächeninhalt $A = \frac {1}{2} \cdot 2,5 cm \cdot 1,5 cm$

Endlich - der Umfang eines Dreiecks:

Bearbeite hierfür B. S. 134/ 1a)! Bitte decke zuerst die Lösung zu. Danke!

Die Lösung zu dieser Aufgabe findest du wie bereits erwähnt im Buch, vergleiche deine Lösung mit dieser und formuliere darüber hinaus in Gedanken einen Merksatz!

Merke:

Vergleiche deine Überlegung mit dem folgenden Merksatz und übertrage diesen in dein Heft!

Umfang eines Dreiecks

Der Umfang U eines Dreiecks ist gleich der Summe seiner drei Seitenlängen: $U = a + b+ c$

FREIWILLIG:

Falls du noch etwas das Zeichnen von Höhen im Dreieck trainieren möchtest, kannst du dies mit folgender Übung tun.
Die beiden Kreuzchen auf den Geodreieck ermöglichen es dir das Geodreieck zu drehen und zu verschieben.
Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite - z.B. indem du "F5" auf der Tastatur drückst, dann sollte es normalerweise klappen...

04.03.2021

Zur Wiederholung:

Sei dir zunächst zu 100 % sicher, dass du die Formel zur Berechnung des Flächeninhalt eines Dreiecks und die zur Berechnung des Umgangs eines Dreiecks weißt. Sonst lies dies bitte im Heft nach, bevor du mit den Aufgaben beginnst. Danke!

Übung:

Bearbeite B. S. 137/ 15! Lies die Aufgabenstellung genau, nicht dass du zu viel rechnest!
Anmerkung: 1 Kästchenlänge $\hat{=}$ 1 cm!

Vergleiche deine Lösung mit meinem Lösungsvorschlag, verbessere gebenenfalls und achte hierbei besonders auf die Einheiten!

Lösung der Aufgabe:

Berechnung des Flächeninhalts von Tobias' Dreieck:
$A = \frac{1}{2} \cdot g \cdot h = \frac {1}{2} \cdot (5 cm \cdot 4 cm) = \frac{1}{2} \cdot 20 cm^2 = 10 cm^2$

Erklärung:

Der Flächeninhalt hängt ganz alleine von der Grundseite und der zugehörigen Höhe ab. Sowohl Hendrik, als auch Tobias haben jeweils eine Länge von 5 cm für die Grundseite gewählt und für die zugehörige Länge 4 cm.
Die Längen der anderen Seiten des Dreiecks haben keinerlei Einfluss auf den Flächeninhalt des Dreiecks!

Übung:

Endlich mal wieder eine Textaufgabe... Ich weiß du freust dich sehr ;-)
Bearbeite bitte im B. S. 137/ 18!
Falls du nicht sofort weiter kommst, kann dir der folgende Tipp sicher helfen.

Tipp
1. Der Giebel ist die orangene Fläche. Berechne also die Fläche des orangen Dreiecks...

2. Um die Kosten für die Holzverschalung zu bekommen, muss man den Flächeninhalt des Giebels mit dem Preis für einen m² Holz - 47,50 € - multiplizieren.

Lösung der Aufgabe:

Berechnung des Flächeninhalts - oranges Dreieck:
$A = \frac{1}{2} \cdot g \cdot h = \frac {1}{2} \cdot 14,8 m \cdot 6,8 m = 7,4 m \cdot 6,8 m = 50,32 m^2$

Anmerkung:
In einer Nebenrechnung berechnet man $74 \cdot 68$, das Ergebnis ist hier 5032. Das Ergebnis für den Flächeninhalt des Dreiecks ist somit 50,32 m², denn die Zahlen 7,4 und 6,8 haben gemeinsam zwei Nachkommastellen.

Kosten für die Holzverschalung:
$50,32 \cdot 47,50 = 2390,2$ [€]

Anmerkung:
In einer Nebenrechnung berechnet man $5032 \cdot 4750$, das Ergebnis ist hier 23902000.
Die Zahlen 50,32 und 47,50 haben zusammen vier Nachkommastellen, daher erhält man als Ergebnis 2390,2(000) = 2390,2!

Antwortsatz: Die Kosten für die Holzverschalung betragen 2390,20 €

Übung:

Mit B. S. 138/ 23 kannst du testen, ob du das Rechnen mit Umkehraufgaben verstanden hast. Hier ist nämlich die Höhe h_b gesucht.
Tipp: Starte zunächst mit der Berechnung des Flächeninhalts des Dreieck, indem du die Grundseite a und ihre zugehörige Höhe h_a verwendest. Somit bist du der Lösung schon einen gewältigen Schritt näher gekommen...
Vergleiche dein Ergebnis zum Flächeninhalt bitte, bevor du weiter rechnest, mit meinem!

Flächeninhalt des Dreiecks

$A = \frac{1}{2} \cdot a \cdot h_a = \frac {1}{2} \cdot 8,2 cm \cdot 2,6 cm = 4,1 cm \cdot 2,6 cm = 10,66 cm^2$

Anmerkung:

In einer Nebenrechnung berechnet man $41 \cdot 26$, das Ergebnis ist hier 1066. Das Ergebnis für den Flächeninhalt des Dreiecks ist somit 10,66 cm², denn die Zahlen 4,1 und 2,6 haben gemeinsam zwei Nachkommastellen.

Lösung der Höhe h_b:

1. Möglichkeit:

Berechnung der Höhe h_b mit Hilfe einer Umkehraufgabe, aber zunächst notiert man sich, was gegeben und was gesucht ist und setzt die Zahlen entsprechend in die Formel für den Flächeninhalt eines Dreiecks ein...

Gegeben: b = 3,5 cm und A = 10,66 cm²

$A = \frac{1}{2} \cdot b \cdot h_b$

Einsetzen liefert: $10,66 cm^2 = \frac{1}{2} \cdot 3,5 cm \cdot h_b$

Zunächst berechnet man $\frac {1}{2} \cdot 3,5 cm$ und erhält somit: $10,66 cm^2 = 1,75 cm \cdot h_b$

Mit der Umkehraufgabe berechnet man h: $h= 10,66 cm^2 \div 1,75 cm = 1066 cm^2 \div 175 cm = 6,0914... cm \approx 6,1 cm$

Vielleicht hast du aber auch die folgende Möglichkeit verwendet... Falls nicht, dann bitte einfach nicht beachten!

2. Möglichkeit:

Verdopple zunächst den Flächeninhalt A des Dreiecks: $2 \cdot A = 2 \cdot 10,66 cm = 21,32 cm$

Löse mit der Umkehraufgabe - man teilt den doppelten Flächeninhalt der Dreiecksfläche durch die Grundseite und erhält somit die zugehörige Höhe:
$h_b = (2 \cdot A) \div b = 21,32 cm^2 \div 3,5 cm = 213,2 cm^2 \div 35 cm = 6,0914... cm \approx 6,1 cm$

Vergiss bitte nicht "$cm^2 \div cm = cm$"! Das Ergebnis muss eine Länge sein!

Info:

Nun weißt du bereits schon sehr viel zu Flächeninhalten, du kannst den Flächeninhalt eines Rechtecks bestimmen, den Flächeninhalt eines Quadrats, den Flächeninhalt eines Parallelogramms, eigentlich somit auch den Flächeninhalt einer Raute und den Flächeninhalt eines Dreiecks....
Aber fertig sind wir hier noch nicht, es fehlt noch der Flächeninhalt eines Trapezes. Damit du dich daran erinnerst, was das nun wieder für ein besonderes Viereck war, schaue dir den folgenden Film als Vorbereitung auf die Stunde am Montag an. Dann geht es wieder weiter.

Aber zunächst erstmal ein schönes Wochenende!!

Zur Wiederholung - das Trapez:

EmbedVideo fehlt ein anzugebender Parameter.

Zur Wiederholung:

Falls du es gestern nicht mehr geschafft hast Höhen ins Dreieck einzuzeichnen, kannst du dies ja heute vielleicht testen... Die zugehörige Übung findest du in der gestrigen Stunde am Ende.... Nur ein Vorschlag, auch heute kein Muss...

08.03.2021

Info:

Heute wirst du lernen, wie man den Flächeninhalt und den Umfang eines Trapezes bestimmt.
Für die Herleitung des Flächeninhalts eines Trapezes schaue dir bitte folgendes Video an.
WICHTIG: Sollte dir in der heutigen Doppelstunde irgendein Punkt unklar sein, schreib mir bitte eine Nachricht via Schulmanager. Danke!

Herleitung des Flächeninhalts eines Trapezes:

EmbedVideo fehlt ein anzugebender Parameter.

Übung:

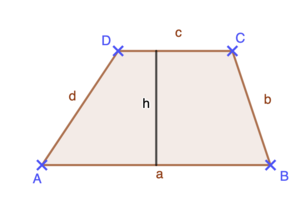
Löse nun die Aufgabe aus den Video! Berechne den Flächeninhalt des Trapezes: a = 7,8 cm; c = 3,8 cm; h = 4,5 cm;

Lösung der Aufgabe:

Berechnung des Flächeninhalts des Trapezes:
$A = \frac{1}{2}\cdot(a+c)\cdot h = \frac{1}{2} \cdot (7,8 cm + 3,8 cm) \cdot 4,5 cm = \frac {1}{2} \cdot 11,6 cm \cdot 4,5 cm = 5,8 cm \cdot 4,5 cm = 26,1 cm^2$

Anmerkung:
In einer Nebenrechnung berechnet am das Produkt $58 \cdot 45 = 2610$.

5,8 und 4,5 haben zusammen 2 Nachkommastellen, daher erhält man für $5,8 \cdot 4,5 = 26,10 = 26,1$.

Merke:

Notiere bitte folgenden Merksatz in dein Heft!

Flächeninhalt eines Trapezes

Ein Trapez ist ein Viereck mit zwei parallelen Seiten.

Den Abstand zweier zueinander paralleler Grundseiten eines Trapezes nennt man Höhe.

Für den Flächeninhalt eines Trapezes mit den Längen a und c der zueinander parallelen Seiten und der dazugehörigen Höhe h gilt:
$A=\frac{1}{2}\cdot(a+c)\cdot h$

Merke:

Bearbeite bitte zunächst B.S. 143/ 1 a) im Heft. Decke die Lösung im Buch ab und vergleiche nach Bearbeitung der Aufgabe deinen Lösungsvorschlag mit dem im Buch. Danke!
Ich vermute mal, die Bestimmung des Umfangs war keine große Schwierigkeit...
Überlege dir noch, wie man allgemein eine Formel für den Umfang eines Trapezes aufschreiben kann!
Vergleiche deine Überlegung mit dem folgenden Merksatz und notiere diesen bitte noch in dein Heft!

Umfang eines Trapezes

Für den Umfang eines Trapezes gilt:

$U=a+b+c+d$

Übung:

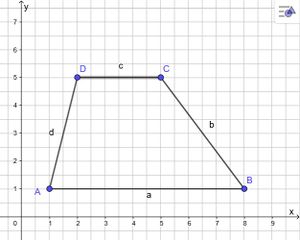
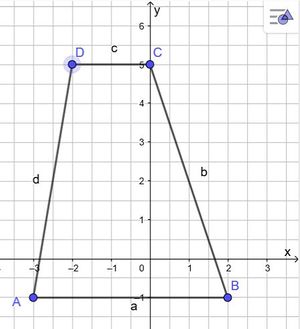
Berechne jeweils den Flächeninhalt des Trapezes! Schaue zuerst sehr genau, um die beiden parallelen Seiten zu erkunden!

Übung:

Bearbeite B. S. 144/ 4 a) und c)!
Bevor du mit dem Zeichnen des Koordinatensystems startest, überlege dir anhand der gegeben Punkt wie viel Platz du brauchen wirst.
Berechne den Flächeninhalt mit Längen, die du eindeutig aus deiner Skizze ablesen kannst!

B. S. 144/ 4 a):

a = 7 cm; c = 3 cm; h = 4 cm
$A=\frac{1}{2} \cdot (a + c) \cdot h = \frac{1}{2} \cdot (7cm + 3cm) \cdot 4 cm = \frac{1}{2} \cdot 10 cm \cdot 4 cm = 5 cm \cdot 4 cm = 20 cm^2$

B. S. 144/ 4 c):

a= 5cm; c = 2 cm; h = 6 cm

$A= \frac{1}{2} \cdot (a + c) \cdot h = \frac{1}{2} \cdot (5cm + 2cm) \cdot 6cm = \frac{1}{2} \cdot 7cm \cdot 6cm = (7 cm \cdot 6 cm)\div 2 = 42cm^2 \div 2 = 21 cm^2$

Übung:

Du freust dich bestimmt, mal wieder eine Textaufgabe ;-)
Bearbeite bitte B. S. 144/ 6!

Gegeben: a = 100 cm; c = 60 cm; h = 70 cm

$A= \frac{1}{2} \cdot (a + c) \cdot h = \frac{1}{2} \cdot (100cm + 60cm) \cdot 70cm = \frac{1}{2} 160 cm \cdot 70 cm = 80 cm \cdot 70 cm = 5600cm^2$

Zunächst musst du den Flächeninhalt des Trapezes in m² angeben: A = 5600cm² = 56 dm² = 0,56 m²
Grund: Die Kosten für die Glasscheibe sind in € pro m² angegeben, und zwar 35€ pro m²

Berechnung der Kosten: $0,56 \cdot 35$ € = 19,60 €

Anmerkung: In einer Nebenrechnung berechnest du $56 \cdot 35 = 1960$.
0,56 und 35 haben zusammen zwei Nachkommastellen und somit muss das Ergebnis auch zwei Nachkommastellen besitzen.

Antwortsatz: Die Kosten für die Glasscheibe betragen 19,60 €.

Zum Abschluss:

Nimm einen Schmierzettel und notiere dir alle Formeln zu Flächeninhalt und Umfang, die du dir in den vergangenen Stunden erarbeitet hast! Vergleiche für jede einzelne Formel deine Lösung mit den entsprechenden Merksätzen im Heft bzw. Buch!
Konntest du dich an alle Formeln erinnern?

Und nun der Test:

Eine Wiederholung und Vertiefung deines Wissens zu Vierecken.... Viel Erfolg!

Freiwillig bzw. Pflicht, falls die beiden Mathestunden noch nicht vorbei sind...

Hier kannst du testen, ob du die Berechnung des Flächeninhalts eines Trapezes verstanden hast. Für mindestens drei Trapeze solltest du dies schon testen!
Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite - z.B. indem du "F5" auf der Tastatur drückst, dann sollte es normalerweise klappen...

Freiwillig

Mit folgenden Video kannst du dein Wissen rund um das Trapez freiwillig wiederholen, vertiefen und sichern. Hier lernst du auch eine andere Variante kennen die Formel für den Flächeninhalt zu notieren... Du kannst die Angaben der jeweiligen Aufgaben gerne verwenden und den Flächeninhalt des Trapezes mit der Formel berechnen, die du heute kennen gelernt hast! So hast du gleich weitere Übungsmöglichkeiten und den Test, ob du das Themengebiet richtig verstanden hast...
Der im Video erwähnte Satz des Pythagoras braucht dich noch nicht zu stressen, der wird dir erst später in deinem Schulleben begegnen...

Zur Wiederholung von Umfang und Flächeninhalt eines Trapezes:

EmbedVideo fehlt ein anzugebender Parameter.