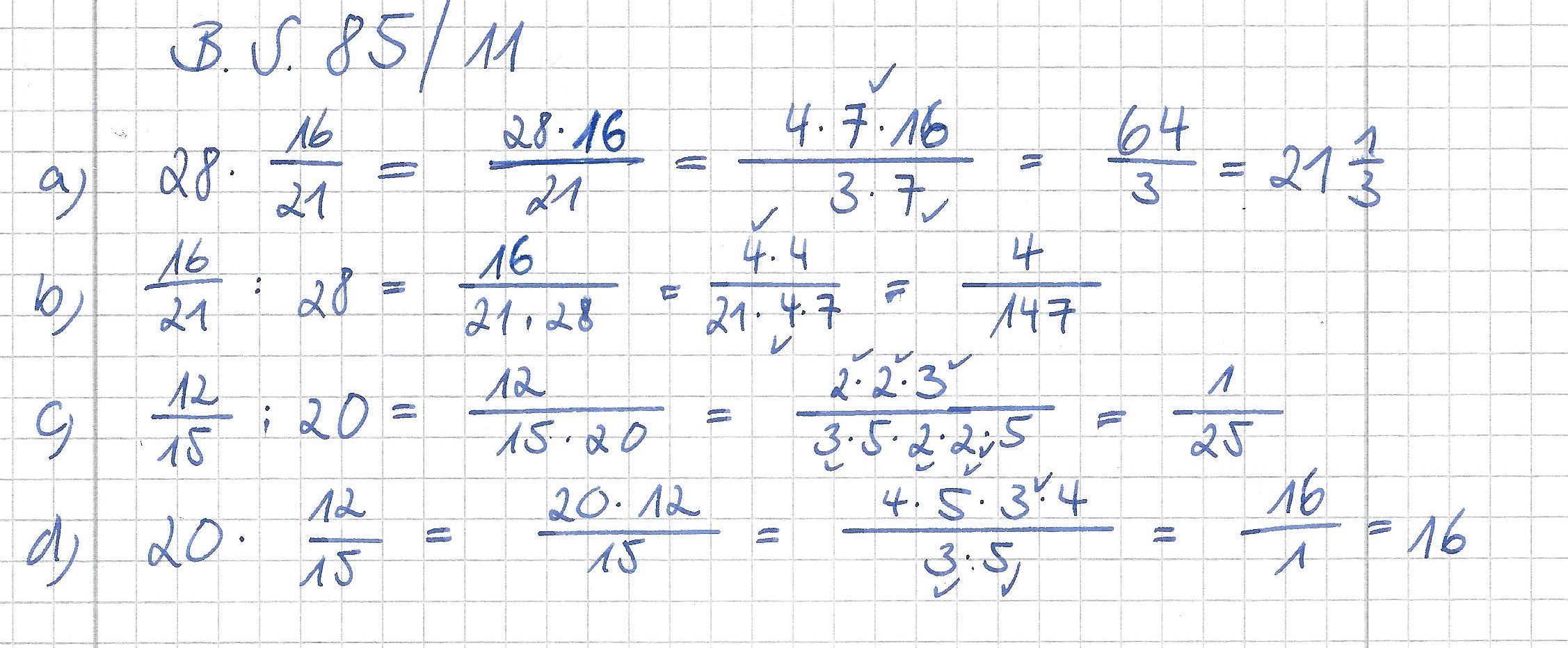11.01.2021

Info vorab:

Idee für die "Pause in Distanz": Weitere Infos du findest du im Schulmanager. Schau doch einfach um 9.30 Uhr mal im Modul "LERNEN" vorbei, wenn du magst.... Das Modul wird auch dann erst freigegeben, vorher ist da noch nichts, du kannst also ganz entspannt arbeiten ;-)

Zum Einstieg und zur Wiederholung ein Kreuzworträtsel - hier kannst du dein Wissen zu Brüchen testen. Viel Spaß!

Zur Erinnerung:

Im Rätsel kam es auch bereits vor, hier nun noch einmal:

Man multipliziert einen Bruch mit einer natürlichen Zahl, indem man den Zähler des Bruchs mit der Zahl multipliziert. Der Nenner bleibt unverändert!

Man dividiert einen Bruch durch eine natürliche Zahl, indem man den Nenner des Bruchs mit der natürlichen Zahl multipliziert. Der Zähler bleibt erhalten.
WICHTIG: VERGISS NICHT VOR DEM AUSMULTIPLIZIEREN ZU KÜRZEN!!

Zur Wiederholung:

Bearbeite bitte folgende Aufgaben im Schulheft: B. S. 85/ 11 a), b), c), d) und B. S. 85/ 12

Nun geht es los mit einem neuen Themenabschnitt: Multiplizieren von Brüchen

Vielleicht hast du dich beim Bearbeiten der Aufgaben zum Multiplizieren eines Bruches mit einer natürlichen Zahl schon einmal gefragt, wie man einen Bruch mit einem anderen Bruch multiplizieren könnte.... Vielleicht hast du dazu auch schon eine Idee? Wenn nicht, dann kommt dir vielleicht eine, wenn du über die folgenden Fragen/ Informationen nachdenkst... Notiere dir hierfür unter der Überschrift Multiplizieren von Brüchen die jeweilige Aufgabe im Schulheft und berechne diese gegebenenfalls!

Berechne ${\frac {5}{2}}\centerdot 12$ !

{\frac {5}{2}}\centerdot 12={\frac {60}{2}}

Gib die Zahl 12 als unechten Bruch an!

12={\frac {12}{1}}

Damit lässt sich die zu berechnende Aufgabe um einen hilfreichen Zwischenschritt ergänzen und lautet somit wie folgt:

{\frac {5}{2}}\cdot 12={\frac {5}{2}}\cdot {\frac {12}{1}}={\frac {60}{2}}

Überlege dir nun eine Rechenregel, wie man Brüche im Allgemeinen miteinander multipliziert! Nachdem du dir selbst eine Lösung überlegt hast, vergleiche diese mit dem Merksatz und notiere den Merksatz bitte in deinem Schulheft!

Merke: Regel über die Multiplikation von Brüchen:
Brüche werden miteinander multipliziert, indem man Zähler mit Zähler und Nenner mit Nenner multipliziert.

Auch hier gilt: Vergiss das Kürzen nicht, bevor du ausmultiplizierst!

Teste nun, ob du die Rechenregel verstanden hast...

${3 \over 7}\cdot {3 \over 5}$ = (! ${6 \over 35}$ ) ( ${9 \over 35}$ ) (! ${9 \over 12}$ )