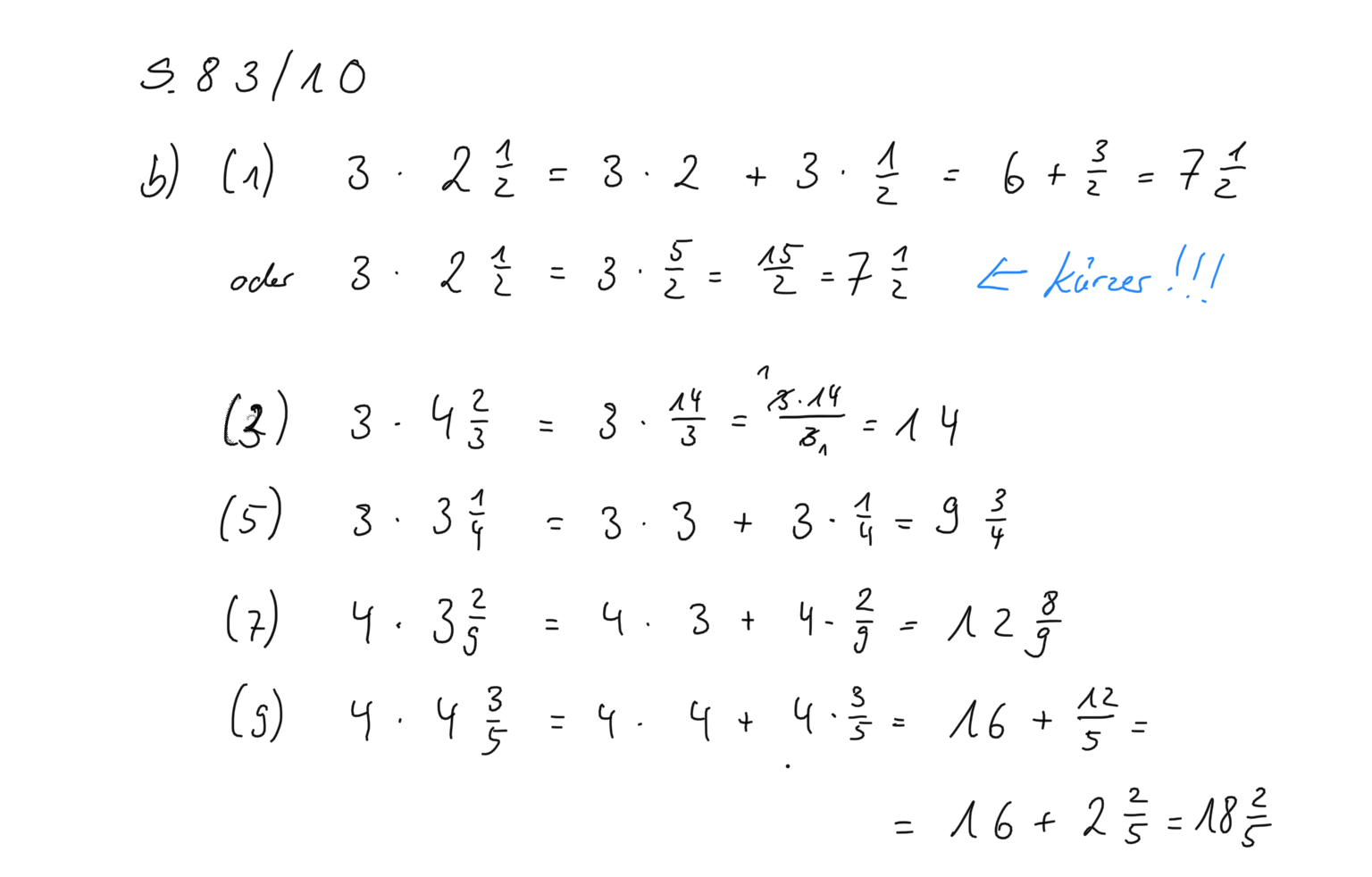6B Vor Weihnachten
Einen schönen guten Morgen!
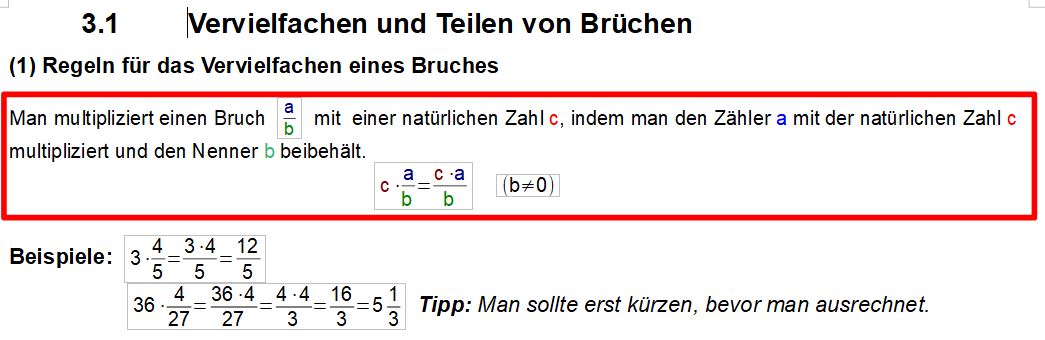
Berechne folgende Aufgaben im Kopf und kürze, falls möglich.
= (!
) (
) (!
)
= (!
) (
) (!
)
= (!
) (
) (!
)
= (!
) (
) (!
)
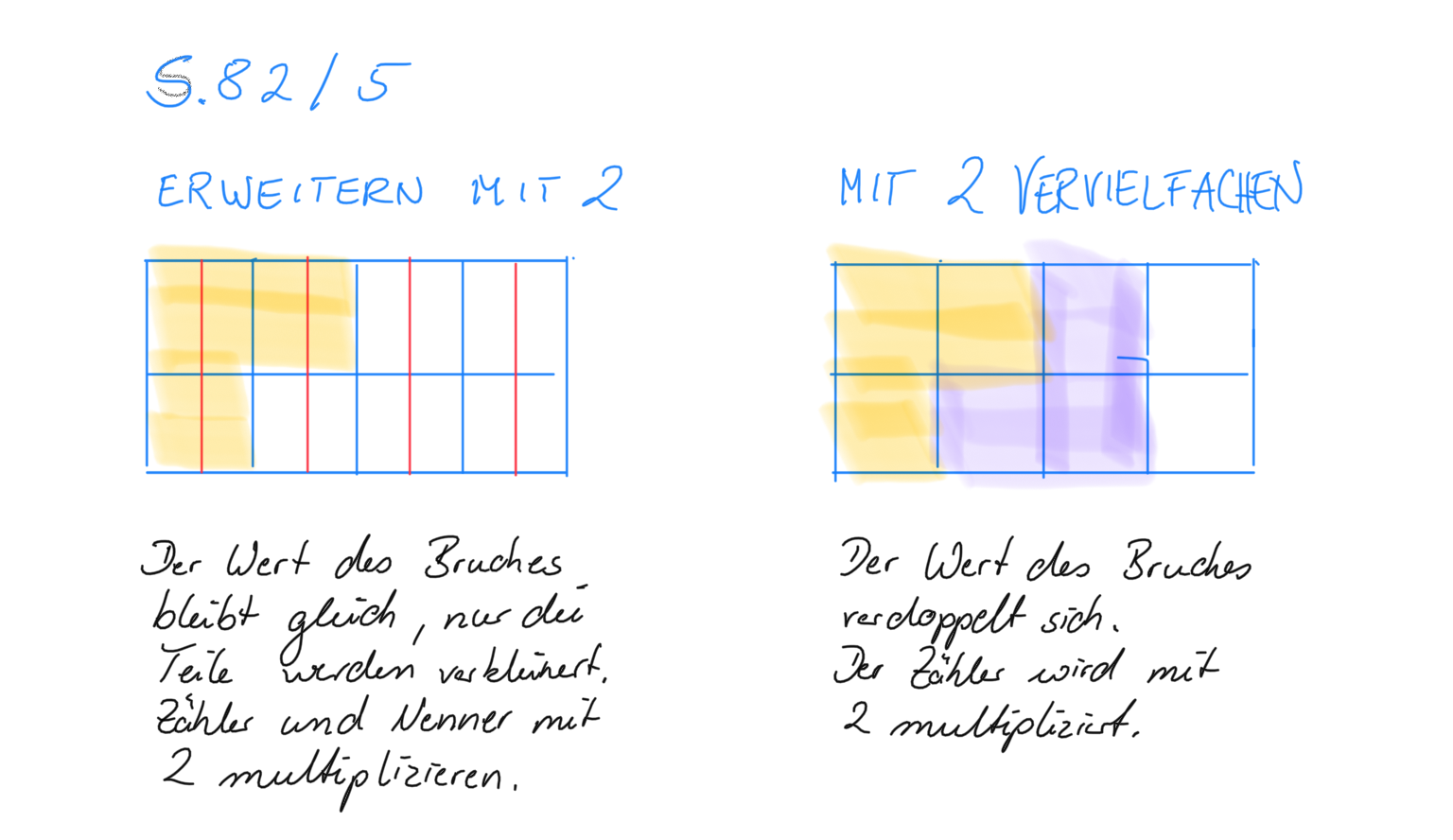
Wir brauchen uns nur den Zähler anzuschauen, wenn der Nenner gleich ist. Denn beim Vervielfachen ändert man den Nenner nicht und nur der Zähler wird vervielfacht.
Brüche in unechte Brüche umwandeln, wenn nötig.
Brüche auf den gemeinsamen Nenner bringen, wenn nötig.
Nun schauen wir uns nur den Zähler an, wenn ihr nicht jetzt schon seht, welchen Wert für x in Frage kommt.
Berechne folgende Aufgaben im Kopf und kürze, falls möglich.
(!x = 1) (x= 2) (!x=4)
(!x = 1) (x= 2) (!x=4)
(!x = 1) (x= 2) (!x=4)
(!x = 2) (x= 7) (!x=3)
Teil 2 Donnerstag 17.12.
Zur Vertiefung:
S.83/10a
Bei Marias Lösung ist wird die gemischte Schreibweise in die unechte Schreibweise umgewandelt und dann gerechnet.
Patrick verwendet das Distributivgesetz. Denn
Wende nun beide Rechenwege mindestens einmal an: S.83/10b Nummer (1),(3),(5),(7),(9)
S.82/8
Leo und seine 6 Freunde sind zusammen 7 Personen.
Bearbeite die folgenden Aufgaben in deinem Übungsheft und kontrolliere mit grün oder einem Glitzerstift.
Weihnachten steht endlich vor der Tür.
a) In der Familie wird der Weihnachtspunsch zubereitet. Alle vier Personen trinken 3 achtel Liter Punsch. Berechne, wie viele Liter die Mutter kaufen muss.
b) Nun haben sich die Eltern vom Vater angemeldet und wollen ebenfalls mittrinken. Beide trinken einen achtel Liter. Berechne, wie viele Liter der Vater noch dazu kaufen muss.
c) Bei den Nachbarn trinken die 5 Familienmitglieder jeweils einen viertel Liter. Die Großeltern möchten drei sechzehntel Liter trinken. Berechne, wie viel Liter Punsch die Nachbarn kaufen müssen. Notiere einen ganzen Term.
d) Der Punsch wird in Literflaschen zu 3,95 € verkauft. Berechne, wie viel die Nachbarn bezahlen müssen.
Die Nachbarn müssen 2 Falschen zu je 3,95€ kaufen.
Da wir noch keine Multiplikation von Dezimalbrüchen hatten, könnt ihr die Zahlen entweder addieren oder in Cent umrechnen.
- Addition: 3,95€ + 3,95€ = 7,90€
- in Cent:
cent = 790 cent = 7,90€
Zeichne in ein Koordinatensystem folgende Punkte:
- Das ganze soll ein Tannebaum werden. Gib die Koordinaten von E, F, M, N, P und S an und vervollständige das Bild.
- An der Stelle
hängt eine rote Kugel. Zeichne sie ein.
- Du kannst den Baum nun verzieren und anmalen.
- Schicke mir ein Foto von deinem Tannebaum. Ich freue mich schon.
Wichtig! Diese Aufgabe ist freiwillig. S.83/13
Wenn ihr eine andere Lösung habt, dann könnt ihr mir diese gerne schicken.
a) Der Nenner kann ein ganz anderer sein.
Also der Nenner ist immernoch 2 und 15 ist um 10 größer als 5.
b)
Teil 3: Freitag 18.12. wiederholen
Potenzen werden genutzt, um Aufgaben kürzer darzustellen. Anstatt eines Produktes mit mehreren gleichen Faktoren kann man auch Potenzen schreiben. Beim Potenzieren gibt die Basis den Faktor an und der Exponent gibt dieser an.
Berechne folgende Potenzen. Schreibe dazu zuerst als Produkt.
Beispiel:
a) b)
c)
d)
e)
a)
b)
c)
d)