3.5 Kreis
Fr. 27.3.
Die Begriffe Radius und Durchmesser kennst du aus der Grundschule und dazu hast du einen Eintrag in dein Merkheft geklebt.
Jetzt kommt eine neue Schreibweise:
Damit man nicht schreiben muss: Der Kreis k mit Mittelpunkt M und Radius r.
Schreiben wir dafür kurz: k(M;r)
Notiere in dein Merkheft:
Das üben wir jetzt kurz im Übungsheft. Links kannst du die Anleitung lesen und rechts findest du Bilder zu den einzelnen Schritten. Denke an den spitzen Bleistift.
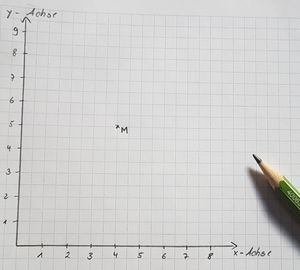
Zeichne den Kreis k(M;3) mit dem Mittelpunkt M(4|5).
- Zeichne ein Koordinatensystem.
- Markiere den Mittelpunkt M(4|5).
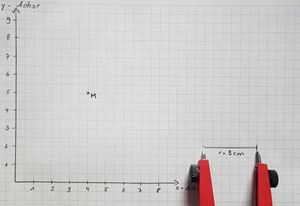
- Stelle auf eurem Zirkel 3 cm ein.
- Steche in den Mittelpunkt M ein und zeichnet den Kreis von 3 cm.
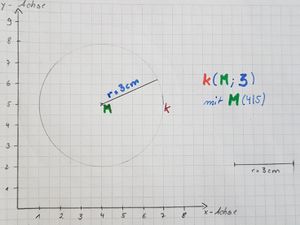
- Zeichne noch den Radius ein und beschrifte ihn.
So sieht das dann aus ...
Sieht auch dein Kreis so aus, dann zeichne ihn auch in dein Merkheft und schreibe „k(M;3) mit dem Mittelpunkt M(4|5)“ daneben
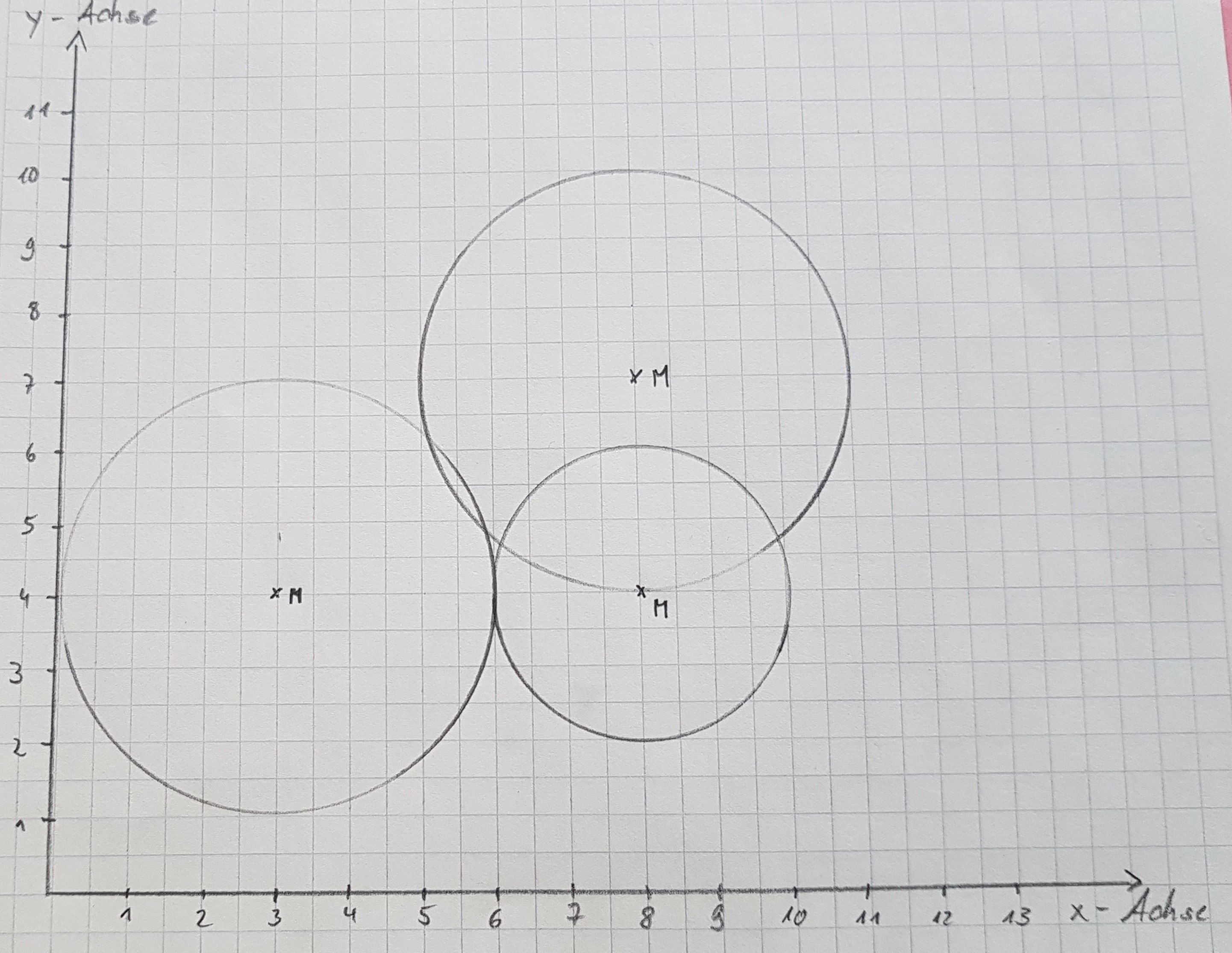
Nun zeichne in das gleiche Koordinatensystem den Kreis k(M;4) und k(M;2) mit dem gleichen Mittelpunkt wie eben.
Und weil es so viel Spaß macht!
Üben
Zeichne ein neues Koordinatensystem mit folgenden Kreisen in dein Übungsheft:
a) k(M; 3) mit M(8|7)
b) k(M; 3) mit M(3|4)
c) k(M; 2) mit M(8|4)
Das hast du super gemacht!!!
Jetzt schicke mir ein Foto von deinem Eintrag ins Merkheft mit deinem Kreis.
Mo. 30.3.
Aufgabe 1
Schau dir die beiden Videos an und notiere dir Fachbegriffe und Schreibweisen, die neu für dich sind.
Aufgabe 2
Fülle das Arbeitsblatt, das ich euch geschickt habe, mit Hilfe deiner Notizen, den Videos und im Buch S.142 aus.
Überprüfe nun deine Lösung.
Verbessere, falls nötig, und klebe das Arbeitsblatt in dein Merkheft.
Aufgabe 3
Alle Punkte, die von einem gegebenen Punkt M die gleiche Entfernung haben, liegen auf einem Kreis.
Der Punkt M heißt Mittelpunkt des Kreises.
Der Abstand der Punkte auf dem Kreis zum Mittelpunkt heißt Radius des Kreises, kurz: r.
Statt "Kreis mit dem Mittelpunkt M und dem Radius r" schreibt man auch k(M;r).
Eine Sehne ist eine Strecke, die zwei Punkte auf dem Kreis verbindet.
Eine Sehne, die durch den Mittelpunkt verläuft, heißt Durchmesser, kurz: d.
Ein Durchmesser eines Kreises ist immer doppelt so lang wie ein Radius, kurz: d = 2·r.
Eine Sekante ist eine Gerade, die den Kreis in zwei Punkten schneidet.
Eine Tangente berührt den Kreis in genau einem Punkt.
Eine Passante hat mit dem Kreis keinen gemeinsamen Punkt.
Aufgabe 4
Bearbeite nun in deinem Arbeitsheft S.41/17 und 18a-c, die Nummer d ist freiwillig.
