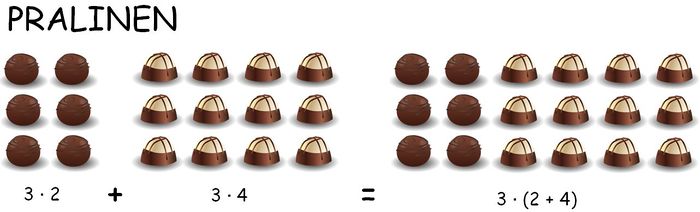5b 2020 21/Rechengesetze
Das Distributivgesetz ist ein weiteres Rechengesetz. Es wird auch Verteilungsgesetz genannt.
Beim Ausmultiplizieren wird jeder Summand der Summe mit der gleichen Zahl multipliziert.
Bsp.: 5 ⋅ (30 + 4) = 5 ⋅ 30 + 5 ⋅ 4.
Beim Ausklammern kann der Faktor, der mehrmals in einer Summe vorkommt, ausgeklammert werden.
Bsp.: 8 ⋅ 13 + 8 ⋅ 27 = 8 ⋅ (13 + 27)
Das Distributivgesetz nutzt man, um vorteilhafter zu rechnen.
1) 3 ⋅ [14 + 5] (!3 ⋅ 14 - 3 ⋅ 5) (3 ⋅ 14 + 3 ⋅ 5) (!14 ⋅ 3 + 14 ⋅ 5) (!5 ⋅ 3 + 5 ⋅ 14)
2) [8 + 12] ⋅ 6 (!8 ⋅ 6 - 12 ⋅ 6) (!8 ⋅ 12 + 12 ⋅ 6) (!6 ⋅ 8 + 12 ⋅ 8) (6 ⋅ 8 + 6 ⋅ 12)
3) 25 ⋅ [7 - 4] (!25 ⋅ 4 - 25 ⋅ 7) (25 ⋅ 7 - 25 ⋅ 4) (!7 ⋅ 25 + 4 ⋅ 25) (!25 ⋅ 4 + 25 ⋅ 7)
4) [28 - 13] ⋅ 16 (!28 ⋅ 16 + 13 ⋅ 16) (!16 ⋅ 13 - 16 ⋅ 28) (16 ⋅ 28 - 13 ⋅ 16) (!28 ⋅ 16 - 28 ⋅ 13)
5) 9 ⋅ [17 + 8] (8 ⋅ 9 + 17 ⋅ 9) (!9 ⋅ 17 + 17 ⋅ 8) (!8 ⋅ 9 - 17 ⋅ 9) (!17 ⋅ 8 + 9 ⋅ 8)
- Finde heraus, woraus sich der erste Rechenausdruck zusammensetzt. Zähle hierfür die hellen und die pinken Schokobonbon-Packungen und beachte, wie viele Schokobonbons in jeder Packung sind.
- Die Schokobonbon-Packungen werden aufgeteilt. Warum?
- Aus wie vielen Reihen (waagerecht) und wie vielen Spalten (senkrecht) setzen sich die dunklen Pralinen zusammen? 3 Reihen und 2 Spalten, d.h. 3 ⋅ 2
- Aus wie vielen Reihen und wie vielen Spalten setzen sich die hellen Pralinen zusammen?
- Findest du bei beiden eine Gemeinsamkeit?
- Aus wie vielen Reihen und wie vielen Spalten setzen sich die gesamten Pralinen zusammen? Warum wurden die Zahlen so aufgeteilt?
Für Fragen zum Assoziativgesetz