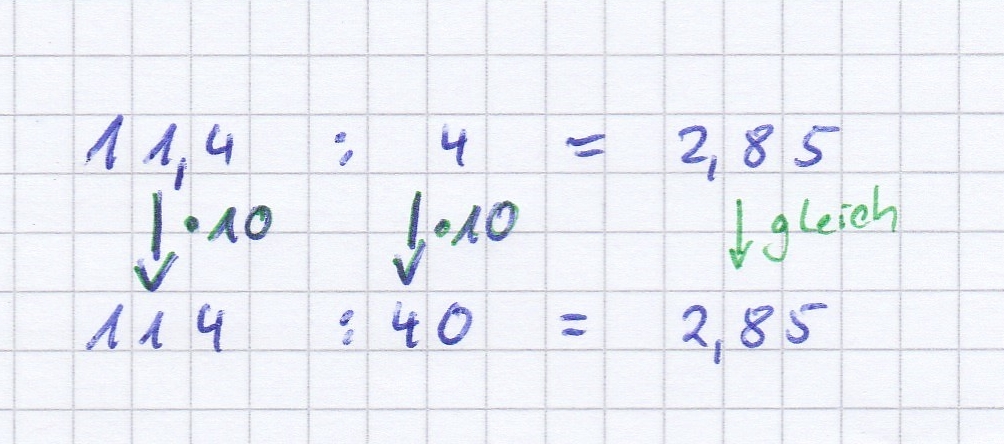M6 3.6 Dividieren von Dezimalzahlen: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 67: | Zeile 67: | ||
|Inhalt= Ihr möchtet aus dem Bioraum raus. Gerechnet habt ihr doch genug, oder? Ihr fragt eure Eltern nach der Lösung, um euch selber zu überprüfen. Welche Fehler habe ich gemacht? Verstehe ich sie?<br> | |Inhalt= Ihr möchtet aus dem Bioraum raus. Gerechnet habt ihr doch genug, oder? Ihr fragt eure Eltern nach der Lösung, um euch selber zu überprüfen. Welche Fehler habe ich gemacht? Verstehe ich sie?<br> | ||
Die Tafel vor dir verändert sich. Die Kreide ist weg und | Die Tafel vor dir verändert sich. Die Kreide ist weg und es erscheinen Matheaufgaben. | ||
[[Datei:Tafel-Auftrag zu periodischen Brüchen.jpg|600px|center|rahmenlos]] | [[Datei:Tafel-Auftrag zu periodischen Brüchen.jpg|600px|center|rahmenlos]] | ||