9a 2020 21/Chemie: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Seite angelegt) Markierung: Quelltext-Bearbeitung 2017 |
(Quarantäne-Einheit 1 hierher verschoben) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
==Chemie== | ==Chemie== | ||
===Quarantäne-Einheit 1=== | |||
''Für die folgende Einheit benötigt ihr: Das Schulbuch, eine Internetverbindung, Stift + Zettel und Ruhe. Die Arbeitszeit sollte 45 Minuten nicht übersteigen.'' | |||
<br> | |||
{{Box-spezial | |||
|Titel=<span style="color:#080">'''Das Teilchen-Modell der Materie, Teil 1'''</span> | |||
|Inhalt= | |||
Wir haben im Unterricht schon ein paar Mal angesprochen, dass Materie aus „Teilchen“ besteht. Bei den Aggregatszuständen zum Beispiel haben wir kleine Kugeln zur Darstellung verwendet. Das ist für euch jetzt wahrscheinlich keine wahnsinnig neue Erkenntnis, denn z. B. die Begriffe „Atom“ und „Molekül“, die eng mit dem Begriff des „Teilchens“ zusammenhängen, habt ihr vermutlich schon oft in den Medien gehört.<br> | |||
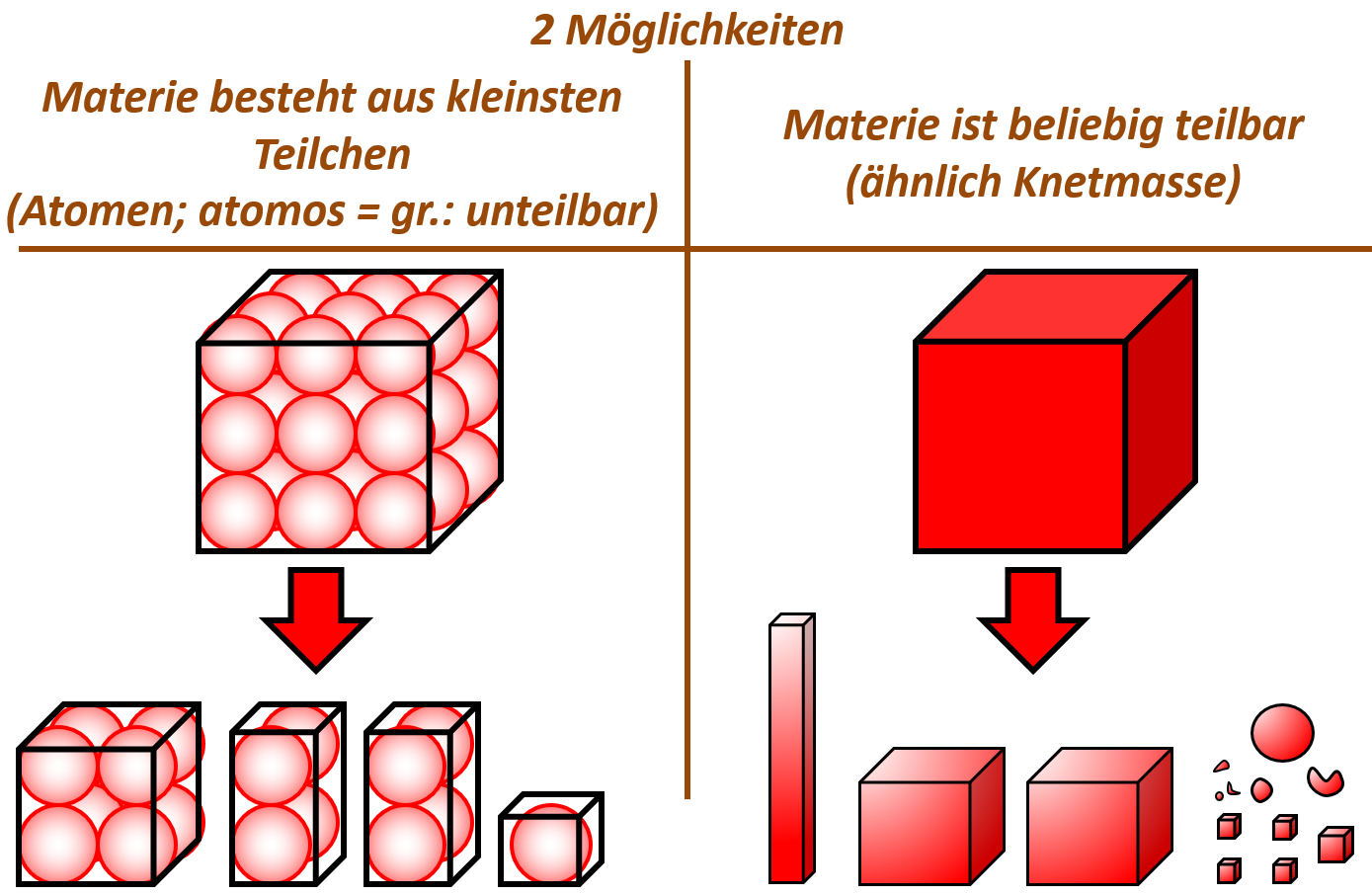
Tatsächlich war schon der griechische Philosoph Demokrit 400 v. Chr. der Meinung, alle Materie bestünde aus winzig kleinen Teilchen. Er nahm an, dass man bei extrem starker Vergrößerung von Materie auf kleine Teilchen stoßen würde, die sich zwar voneinander trennen lassen, selbst aber nicht teilbar sind. Diese Vorstellung nennt man „Teilchen-Modell“. Die unteilbaren, kleinsten Einheiten nannte er „Atome“. <br> | |||
Vielleicht fragt ihr euch jetzt: Na ja klar, wie sollte es denn auch sonst sein?<br> | |||
Tatsächlich gab es noch eine andere Vorstellung: Das „Kontinuums-Modell“. In diesem Modell nahm man an, dass Materie beliebig teilbar ist, ähnlich wie Knetmasse. Nach dieser Vorstellung gibt es keine kleinsten Teilchen, die sich nicht teilen lassen. Jede noch so kleine Stoff-Portion könnte man immer noch weiter teilen.<br> | |||
[[Datei:C9SG_MaterieKlTeil_1.jpg]] | |||
<br> | |||
Schaut das folgende youtube-Video von der vielfach ausgezeichneten Wissenschafts-Journalisten Mai Thi Nguyen-Kim:<br> | |||
In dem Video werden drei Phänomene beschrieben, die wir mit unseren Sinnen wahrnehmen können und die sich mit dem „Teilchen-Modell“ gut erklären lassen. Eure Aufgabe soll es sein, nach dem Video zu überlegen, ob sich die genannten Phänomene auch mit dem Kontinuums-Modell erklären lassen würden.<br> | |||
<br> | |||
* '''Legt Stift und Papier bereit!''' | |||
* '''Startet das Video (Dauer: 4:35)!''' | |||
<br> | |||
{{#ev:youtube|ej7-EbeXpmI}}<br> | |||
<br> | |||
* '''Nach dem Video: Fasst zunächst stichpunktartig zusammen, wie die genannten Effekte mit Hilfe des „Teilchen-Modells“ erklärt werden!''' (Klickt bitte erst auf "Lösung", wenn ihr wirkliche die Aufgabe erledigt habt) | |||
{{Lösung versteckt| | |||
'''Aggregatszustände''': <br> | |||
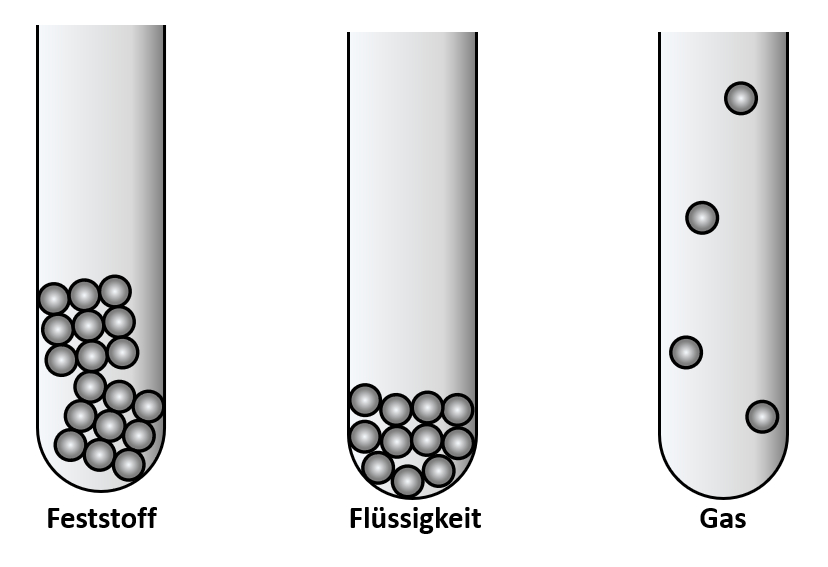
Zwischen den Teilchen gibt es Anziehungskräfte. Wärme führt dazu, dass sich die Teilchen schneller bewegen, sie schwingen schneller hin- und her. Das erklärt warum bei tiefen Temperaturen die Teilchen eng aneinander "kleben" und ihre Form nicht ändern (ein würfelförmiger Pflasterstein bleibt immer würfelförmig, auch wenn man ihn in ein rundes Gefäß wirft).<br> | |||
Das Modell erklärt auch gut, warum sich eine Flüssigkeit beim Verdampfen so stark ausdehnt: Die Teilchen flitzen nun recht schnell durch die Gegend, und haben einen großen Abstand zueinander.<br> | |||
[[Datei:C9SG_MaterieKlTeil_2.jpg]]<br> | |||
'''Wärmeleitfähigkeit''': <br> | |||
Bei Stoffen, die sich berühren, stoßen die Teilchen des einen Stoffes an die Teilchen des anderen Stoffes. So werden Schwingungen an benachbarte Gegenstände oder Stoffe weitergegeben. Das erklärt dann auch, warum eine Tasse nach kurzer Zeit heiß wird, wenn man sie mit kochendem Wasser füllt.<br> | |||
'''Diffusion''': <br> | |||
Nachdem Teilchen immer in Bewegung sind (außer am absoluten Nullpunkt), mischen sich zwei nebeneinander vorkommende Stoffe von ganz alleine (das ist nicht ganz korrekt, es kommt schon auch etwas auf die Stoffe an).<br> | |||
Wenn man lange genug warten würde, müsste man z.B. eine Tasse Tee gar nicht umrühren, nachdem man Zucker hinzu gegeben hat. Schon nach wenigen Stunden hätte sich der Zucker von ganz alleine im Tee gleichmäßig verteilt.<br> | |||
<br> Das war ein Witz! Der Tee wäre dann ja eiskalt... | |||
|Lösung|Lösung ausblenden}} | |||
* '''Überlegt jetzt für alle drei Effekte einzeln, ob auch das „Kontinuums-Modell“ die Beobachtungen erklären könnte!''' (Klickt erst auf den entsprechenden Begriff, wenn ihr wirklich darüber nachgedacht habt.) | |||
{{Lösung versteckt| | |||
Vor allem die Volumenzunahme beim Verdampfen einer Flüssigkeit wäre mit dem Kontinuums-Modell schwierig zu erklären. | |||
|Aggregatszustände|Lösung ausblenden}}<br> | |||
{{Lösung versteckt| | |||
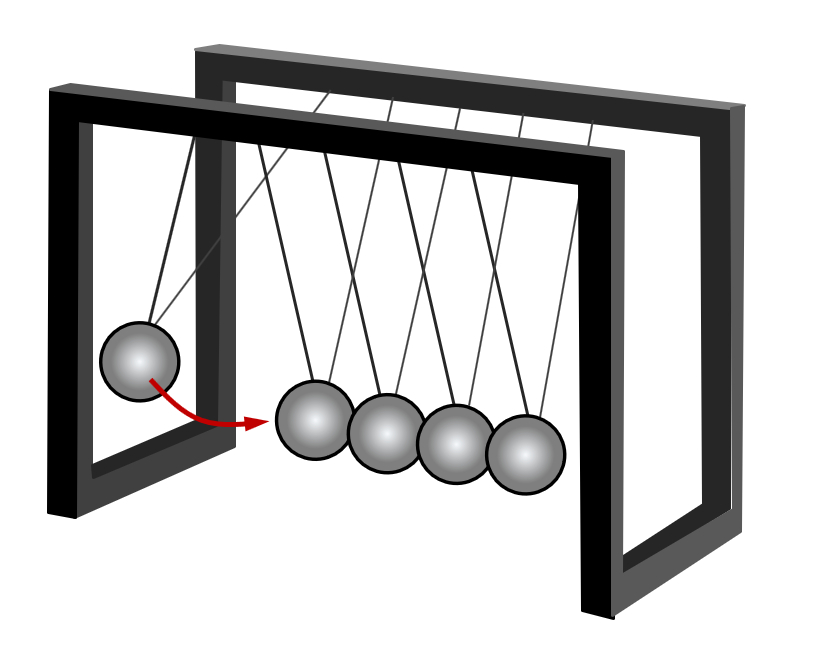
Die Vorstellung von "schwingender Knetmasse" ist eher schwierig. Hier ist das Teilchenmodell wirklich besser: Ihr kennt sicher diese Kugelpendel: Man kann eine Kugel auslenken und loslassen, dann stößt sie an die anderen und gibt so ihre Energie weiter. Das ist einfach einzusehen. Mit Knetmasse würde so etwas nicht funktionieren.<br> | |||
[[Datei:C9SG_MaterieKlTeil_3.jpg]]<br> | |||
|Wärmeleitfähigkeit|Lösung ausblenden}}<br> | |||
{{Lösung versteckt| | |||
Hier sehe ich eher keine Probleme. Auch mit dem Kontinuums-Modell könnte man sich vorstellen, dass sich unterschiedliche Stoffe nach und nach vermischen. | |||
|Diffusion|Lösung ausblenden}}<br> | |||
|Farbe= #080 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #DFB | |||
|Hintergrund= #DFB | |||
}} | |||
<br> | |||
{{Box-spezial | |||
|Titel=<span style="color:#008">'''kurze Pause'''</span> | |||
|Inhalt= | |||
Holt euch einen Kaffee (trinkt man in der 9. Klasse eigentlich schon Kaffee?) oder eben Tee... | |||
|Farbe= #008 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #DFF | |||
|Hintergrund= #DFF | |||
}} | |||
<br> | |||
{{Box-spezial | |||
|Titel=<span style="color:#080">'''Das Teilchen-Modell der Materie, Teil 2'''</span> | |||
|Inhalt= | |||
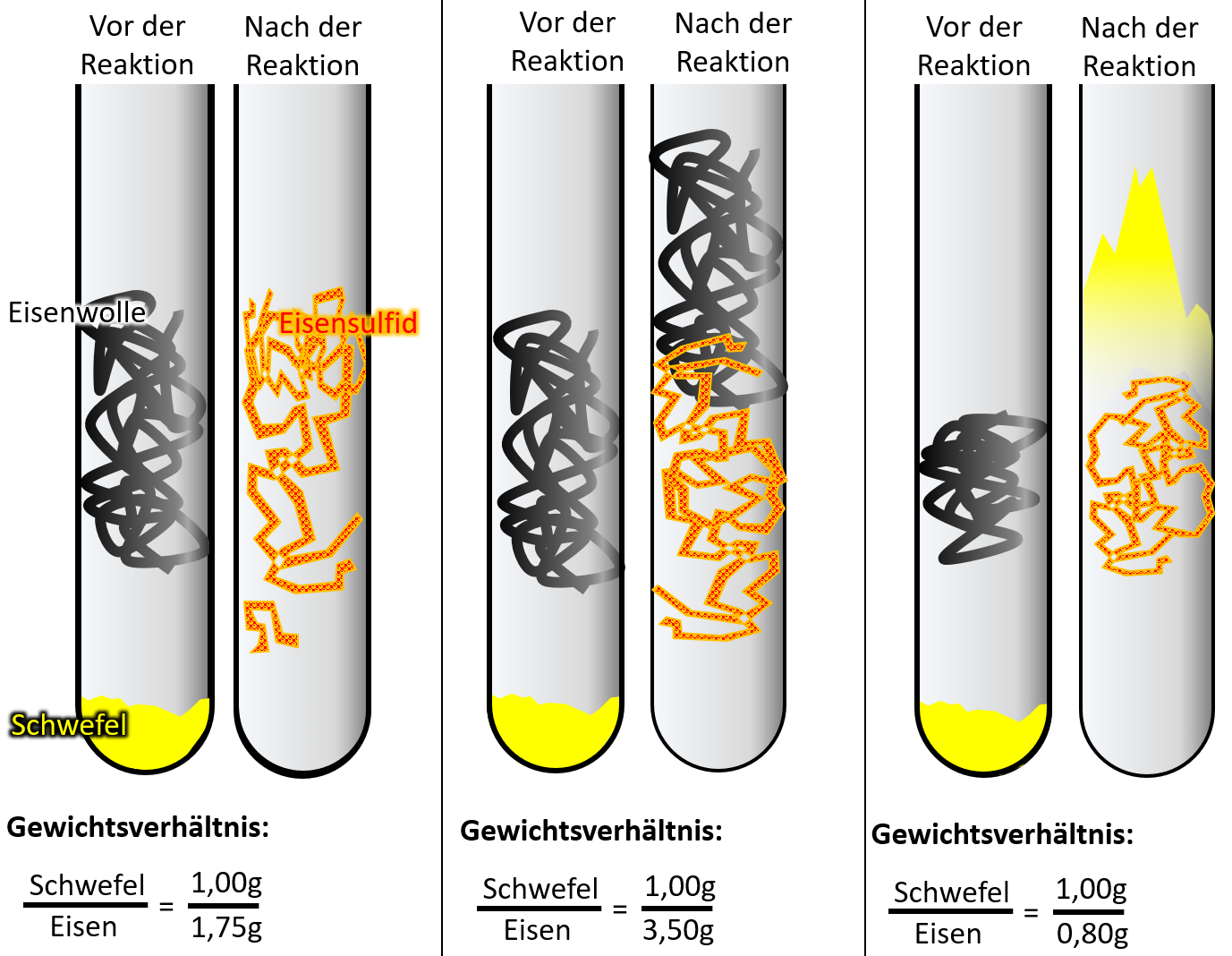
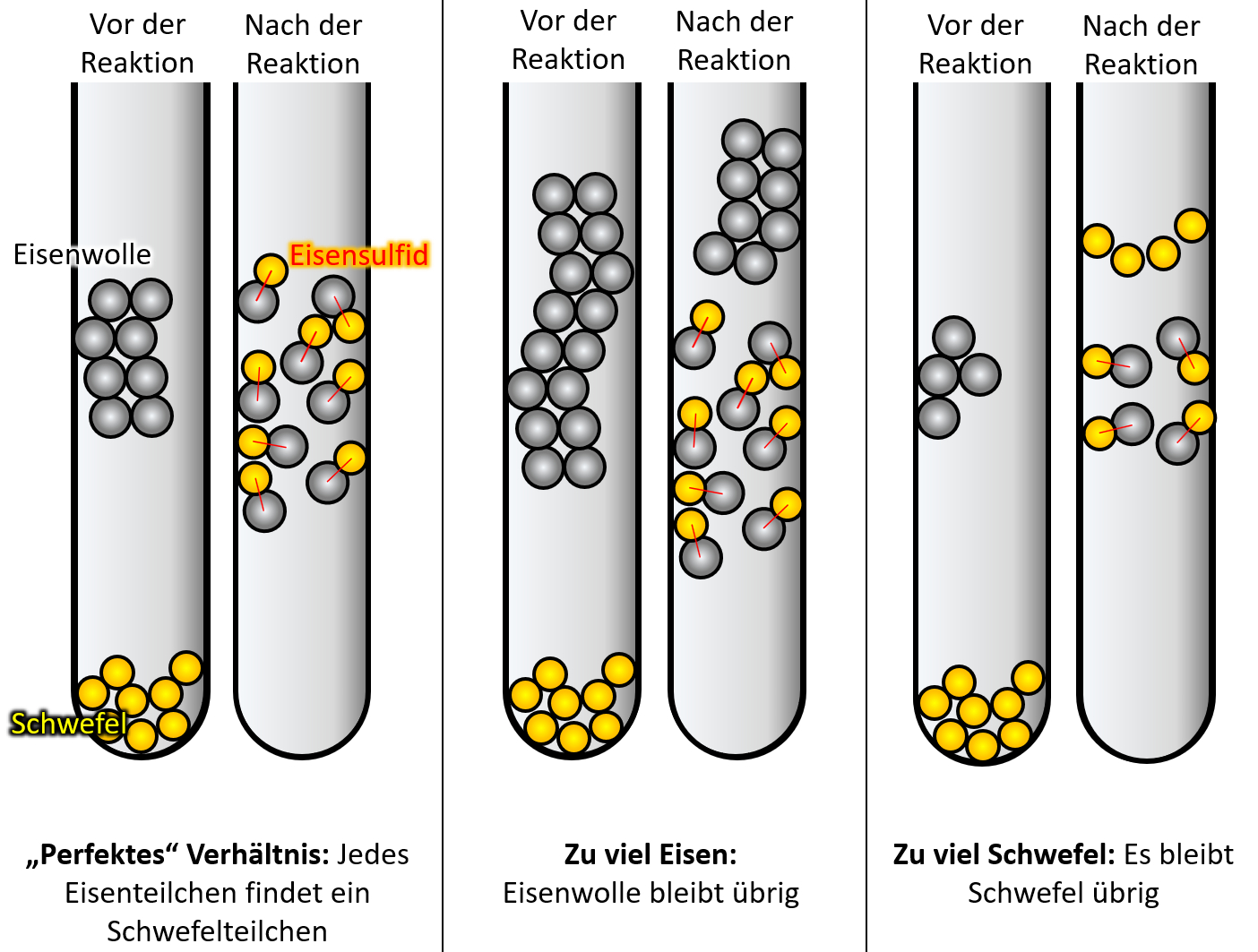
Wenn ihr ganz ehrlich zu euch seid, dann könnte es sein, dass der ein oder andere jetzt noch zweifelt. Sooo wahnsinnig überzeugend ist dieses Teilchen-Modell bis jetzt noch nicht. Der folgende Versuch sollte aber die letzten Zweifel ausräumen. Schlagt euer Buch auf der S. 37 auf. Die Abbildung 3 zeigt einen Versuch, der dreimal mit unterschiedlichen Ausgangsbedingungen durchgeführt wurde: In allen drei Fällen wurde Eisenwolle mit Schwefel in einem Reagenzglas zur Reaktion gebracht. Die Menge an Schwefel war immer gleich, allerdings wurde ist die Menge der Eisenwolle jedesmal anders. In allen drei Fällen entsteht bei der Reaktion ein neuer Reinstoff: Eisensulfid. <br> | |||
Leider ist das Ergebnis auf dem Bild im Buch nicht so schön zu erkennen, deswegen hier noch einmal eine schematische Darstellung: <br> | |||
[[Datei:C9SG_MaterieKlTeil_4.jpg]]<br> | |||
* '''Beschreibt zunächst kurz das Ergebnis!''' | |||
{{Lösung versteckt| | |||
* Im ersten Versuch reagiert der gesamte Schwefel mit der gesamten Eisenwolle vollständig zu Eisensulfid. | |||
* Im zweiten Versucht bleibt Eisenwolle übrig. | |||
* Im dritten Versucht bleibt Schwefel übrig. | |||
|Lösung|Lösung ausblenden}} | |||
* Warum ergibt dieses Ergebnis nur Sinn, wenn man annimmt, dass Materie aus kleinsten Teilchen besteht? | |||
* Was müsste man beobachten können, wenn Materie nach dem Kontinuums-Modell aufgebaut wäre, also so etwas wie Knetmasse wäre? | |||
<br> | |||
* '''Versucht Antworten auf diese Fragen zu finden!''' | |||
{{Lösung versteckt| | |||
Wenn Materie (hier also Eisen und Schwefel) ähnlich wie Knetmasse aufgebaut wären, müsste man jedes beliebige Verhältnis miteinander reagieren lassen können. Nehmen wir an Eisen wäre rote Knetmasse und Schwefel gelbe Knetmassen. Dann müsste es völlig egal sein, wie viel rote Knetmasse ich mit gelber Knetmasse "reagieren lasse" (also durchkneten, bis ein einheitliches Produkt heraus komme. Es sollte immer irgendwas orangefarbenes rauskommen. Mal vielleicht ein bisschen heller, mal ein bisschen dunkler.<br> | |||
'''Das beobachtet man hier aber nicht!'''<br> | |||
Nur wenn man ein ganz bestimmtes Verhältnis von Eisen und Schwefel verwendet, reagieren beide Stoffe vollständig miteinander. Ansonsten bleibt einer der Stoffe übrig. Mit dem Teilchen-Modell ergibt die Beobachtung aber hervorragenden Sinn! Denn wenn ein Eisenteilchen immer genau ein Schwefelteilchen als Reaktionspartner benötigt, dann finden nur bei einem bestimmten Verhältnis alle Teilchen ihren Partner. Andernfalls bleiben Teilchen übrig.<br> | |||
Stelle die Situation in den 6 Reagenzgläsern von oben zeichnerisch so dar, dass man die einzelnen Eisen- und Schwefelteilchen erkennen kann!<br> | |||
{{Lösung versteckt| | |||
[[Datei:C9SG_MaterieKlTeil_5.jpg]]<br> | |||
|Lösung|Lösung ausblenden}} | |||
|Lösung|Lösung ausblenden}} | |||
|Farbe= #080 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #DFB | |||
|Hintergrund= #DFB | |||
}} | |||
{{Box-spezial | |||
|Titel=<span style="color:#008">'''Fertig für heute'''</span> | |||
|Inhalt= | |||
Lest als "Hausaufgabe" (nicht jetzt sofort, macht erst etwas anderes) die Seite 44 und 45 und bearbeitet die Aufgabe 1 (S. 45) mündlich. | |||
|Farbe= #008 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #DFF | |||
|Hintergrund= #DFF | |||
}} | |||
<br> | |||
===Versuchsprotokolle=== | ===Versuchsprotokolle=== | ||
{{Box-spezial | {{Box-spezial | ||
Version vom 22. Oktober 2020, 13:54 Uhr
Chemie
Quarantäne-Einheit 1
Für die folgende Einheit benötigt ihr: Das Schulbuch, eine Internetverbindung, Stift + Zettel und Ruhe. Die Arbeitszeit sollte 45 Minuten nicht übersteigen.
Versuchsprotokolle