Wie nennt man ein Rechteck, das zugleich eine Raute ist?
(!Trapez)
(Quadrat)
(!Drachenviereck)
(!Parallelogramm)
{{Lösung versteckt|1=Das Viereck hat somit rechte Winkel (Rechteck) und alle Seiten sind gleich lang (Raute). Also ist es ein Quadrat.|2=Lösung|3=Lösung}}
</div>
<div class="multiplechoice-quiz">
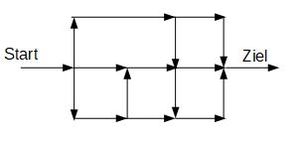
Auf wie vielen verschiedenen Wegen kann man in Pfeilrichtung vom Start zum Ziel gelangen?
[[Datei:FWoche26.jpg|mini]]
(!3)
(!5)
(!7)
(8)
(!10)
Idee der Aufgabenstellung von Känguru 2002.
{{Lösung versteckt|1=9|2=Lösung|3=Lösung}}
</div>
Ihr dürft eure Ergebnisse in den Kopfrechenplan einfügen!
Wie lautet die Lösung der Gleichung 144 : x = 12?
Lösung:
12
Welche der vier Aussage ist falsch?
Ein Parallelogramm kann kein Trapez sein, denn jedes Parallelogramm ist ein Trapez. Es besitzt sogar zwei parallele Seiten.
Ihr dürft eure Ergebnisse in den Kopfrechenplan einfügen!
Kopfmathematik 2
Da im Unterricht die ersten 3 Aufgaben nur mündlich von mir genannt werden, könnt ihr euch die Aufgaben auch von jemand anderen vorlesen lassen. Alle Aufgaben stammen aus der Kopfmathematik vom ISB.
1. Berechne im Kopf: =
360
2. Berechne: 32 * 60 =
1920
3. Runde folgende Zahl auf Tausender: 222518
Lösung:
223000, denn bei 5 als hunderter Stelle muss aufgerundet werden.
4. Betrachte folgende sechs Zahlen und entscheide, welche der unten angeführten Aussagen richtig ist.
15 Millionen
150 Millionen
1500 000 000
(A) Genau drei der sechs Zahlen haben den gleichen Wert.
(B) Genau vier der sechs Zahlen haben den gleichen Wert.
(C) Genau fünf der sechs Zahlen haben den gleichen Wert.
(D) Alle sechs Zahlen haben den gleichen Wert.
(A), denn alle Zahlen mit 7 Nullen sind gleich. 150 Millionen und die beiden Zahlen mit 10er Potenzen.
Ihr dürft eure Ergebnisse in den Kopfrechenplan einfügen!
Kopfmathematik 3
Kopfmathematik
1. Berechne im Kopf: =
121 : 11 - 70 : 7 = 11 - 10 = 1
Alle Zahlen, die durch 2 und 3 teilbar sind, sind auch durch 6 teilbar. Also 1914 und 1092.
2. Welche dieser Zahlen sind durch 6 teilbar?
3. Ein Käfer läuft in einem karteischen Koordinatiensystem die vier Eckpunkte eines Rechtecks ABCD ab. Er startet in A(2|1), läuft dann über B(5|1) und C(5|3) nach D. Die Koordinate von D lautet D(|)
D(2|3)
4. Ein Kind, dass 18 kg wiegt, soll 150 mg des Antibiotika-Wirkstoffs einnehmen. Auf der Verpackung des Medikaments steht 250mg/5ml. Das heißt, dass in 5ml der Medizin 250mg Wirkstoff enhalten ist. Welche Aussagen ist richtig?
Aussagen B und D sind richtig.
Genau diese Rechnungen müssen Krankenschwester, Krankenpfleger, Ärzte und Apotheker täglich berechnen und dürfen sich dabei keine Fehler erlauben.
Ihr dürft eure Ergebnisse in den Kopfrechenplan einfügen!
Kopfmathematik 4
Kopfmathematik
1. Berechne im Kopf: =
64
2. Wie lautet die Lösung der Gleichung 3 + x = -1? x =
Lösung: x = -4 , denn 3 + (-4) = -1.
3. Schreibe die Zahl 580 Millionen mithilfe einer Zehnerpotenz.
4) ist die Lösung, denn (2121 + 1999) : 40 = 4120: 40 = 103.
Ihr dürft eure Ergebnisse in den Kopfrechenplan einfügen! Und heute noch das Kopfmathematik-Spezial
Kopfmathematik-Spezial-Kreuzworträtsel
Klicke auf die Zahl bei dem Wort, das du eintragen möchtest. Es erscheint ein Fenster mit dem Hinweistext und dort kannst du das Lösungswort eintragen.
Waagrecht →
Senkrecht ↓
2
Eine Zahl ist durch 3 teilbar, wenn ihre ... durch 3 teilbar ist.
3
Ein Viereck mit vier gleich langen Seiten.
6
Der Abstand einer Zahl zur 0.
7
Zwei Geraden, die keinen gemeinsamen Punkt haben, sind ... zueinander.
8
Bei diesem Gesetz darf man die Klammern weg lassen. ... gesetz.
1
Mit welchem Fachbegriff bezeichnet man 4 in dem Term 8:4 = 2?
4
Eine Gerade, die einen Kreis in genau einem Punkt berührt.
5
Ändert man bei einer Zahl das Vorzeichen, so erhält man ihre ...
9
Das Vertauschungsgesetz heißt auch ...gesetz.
Kopfmathematik 5
Kopfmathematik
1. Berechne im Kopf: =
-20
2. Gib an, mit welchen Fachbegriffen man folgende Zahlen in diesem Term bezeichnet.
Zahl 6:
Zahl 125:
Die Zahl 6 ist der Exponent und die Zahle 125 ist der Minuend.
3. Wie viele Möglichkeiten gibt es ein Menü aus Vorspeise, Hauptgang und Nachtisch zusammenzustellen, wenn es zwei Vorspeisen, drei Hauptgänge und zwei Nachspeisen gibt?
Anzahl der Möglichkeiten:
4. David geht mit einem 5-Euro-Schein zum Bäcker. Er soll 8 Brötchen, das Stück zu 40 Cent, einkaufen. Für den Rest darf er seine Lieblingskekse, das Stück zu 25 Cent, mitbringen. Wie viele Kekse kann er vom Restgeld höchstens kaufen?
Anzahl der Kekse:
Quelle: Känguru 2007, Kl.3/4, A12
(500 cent - 8* 40 cent): 25 cent = 180 cent : 25 cent = 7 Rest 5 cent, Also ist die Lösung 7 Kekse kann er kaufen.
Ihr dürft eure Ergebnisse in den Kopfrechenplan einfügen!
Kopfmathematik 6
Kopfmathematik
=
9
=
-4
Das Viereck hat somit rechte Winkel (Rechteck) und alle Seiten sind gleich lang (Raute). Also ist es ein Quadrat.
Wie nennt man ein Rechteck, das zugleich eine Raute ist?
Auf wie vielen verschiedenen Wegen kann man in Pfeilrichtung vom Start zum Ziel gelangen?
Idee der Aufgabenstellung von Känguru 2002.
9
Ihr dürft eure Ergebnisse in den Kopfrechenplan einfügen!
Cookies helfen uns bei der Bereitstellung von RMG-Wiki. Durch die Nutzung von RMG-Wiki erklärst du dich damit einverstanden, dass wir Cookies speichern.
