|
|
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) |
| Zeile 11: |
Zeile 11: |
|
| |
|
| {{Box-spezial | | {{Box-spezial |
| |Titel= Unter- und Obersumme | | |Titel= Unter- und Obersumme - Video |
| |Inhalt= [[bild:Int_abb1.png|220px|right]] | | |Inhalt= Eine Möglichkeit ist es, die Fläche mit Hilfe von Streifen zu zerlegen und eine Annährung zu berechnen. Man bildet die Unter- und Obersumme. Eine genaue Erklärung gibts im Video.<br> |
| | {{#ev:youtube|pDHujnO9nvQ|250px}} |
| | |Farbe= #557799 |
| | |Rahmen= 0 |
| | |Rahmenfarbe= #FFFFFF |
| | |Hintergrund= #FFFFFF |
| | |Icon= |
| | }} |
| | |
| | {{Box-spezial |
| | |Titel= Unter- und Obersumme - Beispielaufgaben |
| | |Inhalt= [[Datei:Int_abb1.png|left]] |
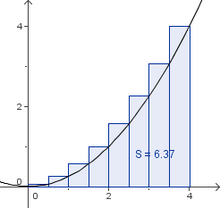
| '''Aufgabe 1''': Gegeben ist die Funktion f(x) = 0.25 x². | | '''Aufgabe 1''': Gegeben ist die Funktion f(x) = 0.25 x². |
| :#Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft. | | :#Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft. |
| Zeile 32: |
Zeile 43: |
| '''Mittelwert: 5,375''' | | '''Mittelwert: 5,375''' |
| |2=Lösung|3=Lösung ausblenden}} | | |2=Lösung|3=Lösung ausblenden}} |
| | <br> |
| | <br> |
| | '''Aufgabe 2''': Gegeben ist die Funktion f(x) = 0.1 x². |
| | :#Zerlege das Intervall [2;5] mit dem Schieberegler in gleichlange Teilintervalle und bestimme die zugehörige Ober- und Untersumme für verschiedene Werte mit dem Applet. |
| | :#Fasse zusammen, was mit der Unter- und Obersumme passiert, wenn die Anzahl der Teilintervalle erhöht wird. |
|
| |
|
| '''Aufgabe 2''': Gegeben ist die Funktion f(x) = 0.5 x².
| | <ggb_applet id="dguq3rpq" width="400" height="310" /> |
| :#Zerlege das Intervall [0;1] mit dem Schieberegler in gleichlange Teilintervalle und bestimme die zugehörige Ober- und Untersumme mit dem Applet.
| |
|
| |
|
| | Falls das Applet im Wiki nicht korrekt angezeigt wird, klicke hier: [https://www.geogebra.org/m/dguq3rpq Link zum Applet] |
| | |
| | {{Lösung versteckt|1= Je höher die Anzahl der Teilintervalle, desto besser ist die Flächenabschätzung. Geht die Anzahl gegen unendlich nähern sich die beiden Werte immer weiter an und haben einen gemeinsamen Grenzwert. |
| | |2=Lösung|3=Lösung ausblenden}} |
|
| |
|
| <ggb_applet width="648" height="588" version="4.4" ggbbase64="UEsDBBQACAgIALigQ0QAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZ1V4B1BTURMuIEqkCKGE3hKiKEFAioJIDZGiSEkgVCHSpApIJ1IUCCUKCohKEVBKKBI6CEgLSJUqJXSIIL1JF178/3/em3dn7rkze+45e3fv7p7v22gD/bssjHyMNDQ0LDracCPqs5l6fwdcoI61gSqmNDRcRzpwdaT/+JqV2RPOkZpf/RvP6iim36aQ1sXzBOXJbc1OnTGuN6MGzzwVUZ6G++Mzrb6pbM9lCmglAWHvtLXRTjfHiehyNvpmETH83vkXYmJhcfFsDjJtXdENHL0LTkN3BmUHJwcHd/6irAYHvYcyao+DF0/Ih0FJJSIrP4s4wtTUqkWnnx0XPdHDacGgBVny1QE7Of6/3jm2xko1iDs4Ogp+G73tt17t+yhaC9YFF5eS4nYZKU4Su/VkJhRtacnJKqTMxhmTYZeUhPBoOMw56e7u5oxiFQapnmw+f3TWVx+0b/nVHwOUuA6WU1CISU0VmEJjPt8EjpPJpKEhzkVD3cAChFwDLqmyrZQM/7jyCt3RuC0AbDg7DcIAu3xgBEQrGORIjwHGKtARcVrDOHTrthxQPNEOt4hrzBMnvg7TArPFopF4cU6+rlZwsl+02ogwVUoK5fvf63NxajBMP0IERIQBbTEYjfLycgN5sElgHiJP1/YyiUTKqqw0qdtq48+Evn8Y8rdiQuRW5DcGY+KrB8FVBWt/j/c13RYXFzXdPCaqRckYArNH7COnWAWCZENBpdNiROXyuCfzSNb4HM844fhTlc/xKblfYaDsRmBxR6BJjmzzwsKn0WrP7BVZuuysVt0LIGMY1c1NnEwxLOHLl3MfZOj/drERaFpEj3x5+FawIjfX0eyD3tvr0cIhJ/27An0FSWX0AyMjV14KqzbMeXCCXDsSFZLrEfS1p6uk8VL72NEqj4yJjPR0EBMT07YfT/Tw8HDO4sHJzg/7xfYLVyUkLHytfa4/1S8/P2Z0KBT4EjCN3RckurYqBe7miUtKJh079qYmCJp33BXGiqlGRUa2jpU5UhQUFEDLB30dMkxqyysrpKn6IM1vBd6HFCEj+W1FkJKLtXX6hKrvaspqn7NdT0+PPJQOcagZdalj7sdib9ob/k6sxvDADwoiYrcciU+9NDZd6yPxIuF6PqCEtdiypnR1tLExVEwNtihTejUFMxsvZuQlFCjx1LzMeVJeXt7L7rn7B/HkDyP2DMm1Dli1zRYfQ/kb8WvkKr1zJUVFknLLmTsSd7gjIciI4uLrBNvWbQUgO7Duu52dHVzu5s0oHE2VUOeYZgkr+KmfH1NniNgEyvly57MSzNDcVO5r/5cAv40pn92T2vEFuX9KIiN6+fEHtQVyRo7tInQehuUrzYoqBzPPE2uj7hE3qca+Wk5ETIkONyUVIAMi4hZmmp577Rk0yaZuLHS8kehl8AwHPE7CZAZdTsfumW1R3f41nPLLpya6wnuxNw/eZ/X5rdRDhTtSE0VQKPTGtaLeKF7wSbBBrHUAhYtcr6w/pfkDKKqq+tB1vFzH/cGdP4n+R79zNafXpvrUU5X8YOjz58/r3LyGysXLQfrQDjHnicEvSZxMmI5LkeLEd8tho0xIcHUO6kQ9X6OlpSW5XsfBOg9dZ/hYk/6ocY0U7skkqPKaEwRC+GRcuz2/t0YeeGmQz2VgT/wyvzpVbzHOSpB8pmnHnyHtD/wdeUWPcmfWuOKzcyLiQuEHtHZii9OXgatxzA7l6osnywVfsthp1fXEVvLhKsFZkJVb2rvPezLH3cmV932fdl/j4uIq1ZwPVgIiydr7V4viKE91g56cY0pjjnUYcnKD0z81qNNWeR2ThQutfFJG0A9e+A6s+TL/kQVxsllpQFSjp3QMRH8cv7wilGOlhkcn1CN+B7LWIN9ozP7fzK3Tow/E45KYC9mANhRIGCM78wWKUZ0dW5gnPQZ6ziWJ0aIFG9F7ttQPeffj1Z98Nju+Yut6pd0HIiJZpTSe91DwRhWVrTsJlTghQqWzsJuMJKGyj6sfBIH7WwhoWnx+MMcxjbIoH5QprMRT6hBuhssGHgXFgu1PJAmSL2c9hrEDZPP6XG9v72JlCUAJuAK/WxiX7vIpKCZoaaiMsQewtIlewA9bbP4BDxpQ1mVJ4ehn7eYOkJPdwQeZWCwtEyp7iGSklW7Y9bNnJQZpOa5tkGjaMd/+yt7WGjodvHMfoOeRyyijHHxgsH4Fo9mH3pMxCQioueU59+JeSOONn6enzxQb1VFN72k5b6uNy3uFfrw485XQgMcuMOTrTs5ODyvGDVT6WEoYmZldNZYf2tY/yeDl5WVn4CpQPVzgCBB4H+Ocy41RQwrsSQJm+cF9fxyFk5dxx/sb3Ld9V+OXpbZDFVxHRX4WW0lUuk9eu82nxM4+pQaCjcC3zn1St2m6ND6v/B8luI/zzb+Y325mMRq0qMNSHz6GaE+0dNM0nZ3v6O5mrhhkkgm9NTY2lrnXIEL3XH3PVvTipWxJJXYlkNIl9hVpQhbkWhSgU959qs6sklzm+EqMbk/9ZSy3VOffzY1lAZ6kFq12FF14PvMIVQELC4uX58BwgamWsfEbMcFOJKacwXA6cEVSkcMWYbC2q8GcnZ29fcRuqPoOM+ttWCk0BJ28MISSFxgJKdOcZPoiGQG8bVSEKiBkT+nb2lyWLrAn8Yah05ubV4EA+jlwKv+IFn8YutgWuixtQ02suWYja84rI0fvrUwLR2stOLMsc2oluNpnLpNq+q3PX/qz1yBKNw/Ys23qomvy0q2/DtOtagRUtOBjqB9euzTaLzaBJXy952N6jdnHP8vG8uFX3/vFTs9NdT02+MF5S6I8xTkaWKQMI7MZr490zEfBp0jKQCwoX47/s0ggyi0be1LEV19oo+jJWlZaunBlIjvQCs1TfCC89iS74e8eeVvgaEngpeD1/olcNorngFV+9XU2WjplTgFjhaj1zG0u4ObM5se+LeIJ6ycnNzeWO2JYu5aNpU9paWlefCzCv0Wqw/xxPFubbP0XOiIIeKW3fGNgvFGgdLtryJMn0nKB0FgAwBWFQkXX1tba+9huhTSdfxzFX5GXp51+bt+IW9DCL+0aGO6VsXzdeDIpcLY5gi1gRoF0hlMIDJrORwBSgg9mo0QrN8Yr9E4d5Epn/e6RbkUCHh1oMzS1XKCdwu5bHYpQNb/4p1mXBSen+7tJoAyr1WBXYOugJ53knpHHj4IW80Y3v/ylVOGs+XskYi+avs+oDd3WczvktE6Ato9WBiPyEUPdmicHc8KCSNxM0Mdvfi/G/hk2pbQg+JUFhhFpTEqPyw11WX+lrD13PcLsPvWlG51V8jmqNerEOj+FDMk8VakTsbr/ysTd3N9wbPMbkU/6Bjn3eGhKv/saiIoabLiYGEme/6k3F3PQVDwxJUZnrUx7dqPSpkTi6cQ6DT+9+pdNEQsw+8W3+ZCpNipCmSEgw+t8ob7nR3dHfoAxvEJ2g+c8l4Pjo6OjDWj007KrqkxPv20iZzfAs2B0khOhBGX7PoYVR3N2x/r+i5SwmE6NVUCJ6I3Cb89AxKhNkQ9COOPF5yJGde6Ttfb+KYZs0djFNL+FadHLtpGxtyKbfcyr/acZ4GqO6qRfIQzZpxyhRInGHOri9pbnroEi+mms279zM3TBGJDhotoAt9fjeHTOaS8zd5hSRFevDhieFB3tMnda/9UraHfJtlvpEYxWITv/JywvJyvLob/fqRppmsfX3wcxWebpCuxo33RVr30QTfGDtbx+FVj5kQwVBsp5FixkX/uyhOi4m6frnhSc+u6dJ8VMPZRi0nF3QtNUTyXSkekGKXzOT0byMG/l0T2iSPI0MQWjTq3gLnAYJiARsBvGIcGLTreqewDD1ERTFMG3zOJi0K1ZztTpfvRlENEoDjCbBKXio5sl1Q7v0K3shRj1zL5/M8p69DkMt5775FZawH7uj9f2oNK5uU/3GqTWMxdxNiblyehoW0mkT2y7rJ8ref2VPq4p6xzG5kGy1LooKluuqfQNQEQ9RL2ymnxTrNbPwUDeSyNFaIY52QpOc/GCyo8kscaf3262c+/HXwU9DrdnAK6/iut6N6P/IAQHwAbtHc5RoU+Ws91jC8vlk/qAIE16A34URFeX6lWai5F6Z8Rw+tHIsksHc6fSJPD9kjloc0+ZY+sTncZ4+tFAlZ490h0xoPYLnFho7FAcvRgdaZ/QH+z4ttrEAphAj8Q7NR6No9PdFaE5Hx5oQWnx9gwR68aOJYXstif+SdX945ho+oanGctQYcNpwBed+xeAVNTEnMwFZhYYk3KvTCPeo3M9x3uM9WRl0VPJGrCytc1UXvftuIuK6ce/fuX/4asFVNjR0dFK4jDP2j2rKu2aM8d+cU9M1Bvvub2+TyetfquqtSpXwgPeYep+l69ODK69bS3qUpeZnryyvxW9Mdq+cVPKt5PlmLtq9WnRAmQ9swAqfFtJaYFJeojf+hbkwA/h/8TH3LJ3SgxUGy7TQ9/wAbgr5VBx9hhyMIhQmzIYOX01f5nWGLbUoRPwpV/D0YCZK6QS5iGejremejBa/8W7nDeG5+xNbrYBBdgRyWlNRvCUk1LEvXTXkgj6OFiZd44YMFJvBxMDjAcg8a/Bfg9YcB7vowTHrlmfGsgJO7O7UbIr3X2EOQ3ks2hdpH5OcpyrLARrutq8c1yaUTDcMv/Mo3rb9dikRkXtkeKwpZ11eym13CV2tNZ0pXmZQZU1uVycBUU1hjO2sVt1aFKzJtoXSGs4398JmeskZsVf3+AEOp+mbsQuag1/jyIYPlAvPjhqjrBHFBnDPzq38jZ5yzZjznCWpsojngERflGydG4vykuA7pI9NH/v7ukF0Vz0cgeGKdChID/yENoZDSYhsKHfqGRxVDbnZQ0lvUK42i9xI6j7wzpO+U0KVdW01C6p3tFuTBNNZKNlWgnakWV+82vInPYmbpMUGXIwF5AAuKpND8tNVbZNl4KDDeS3K5zpUXlSqrK/KInUWIIdt6HTH7uBIJ8Pk3+y9qFzjoferg9mZmdI7jBqkZdU/tACeQwsrL2fzmi/TNlYitNhacYEXRjK4zvUkOfzONBg5hKOccHToCC9gKuqENjeJVxDi5mEV8QtiDSp2Rsdi9cTXBuyuUe21JR2/kAw9YbPpxt55rjKZRblOzmRiEXfVO7yhxES6tFbyOSf3F080C6WtwvRhJFt19+pWHyaxEu3Yx9q7kjA+/RU9vb2Yo6Ojj6xiXK19nLv4IcTJd0+G2HzA+o7E3qXxYDBHHelrx3iGP0YWIUS2yevH+Z1qtQabhv+BbnwqrPZPjuorQ76E+kvJy9195iBo2rhsp74dcEWDyeIaYwktncPL+kStBP8tTqxDNWdrnoF0iTLrSQGlH7Pmr4ONDVnWDh10vvG477Mgt9+nltLyUE8O8kZp8LA2y5k0/LJ7QLZSLdHil8MyaVnt2fMO9prahT99FTWqbj52YO2uHjGq6CtboAfIpdyZTnuktCYVBvLHJ1vD4DwplYGcnCD1MwEFf5byHe/KhUE4YrIgYLy+aCG8lnEVWUgG89KZ9frx+wJE+m+wLC2G5O5xTZm0OYqjrLSBvEhkexyhlwcDXZKEtyHfd9GKy8BT1GZFH+zgAx8YRjfdRXcWO0TC2DOo7KiEA5K/w+TPHXEY1YknvoH3RFqBoVSUi270OBUIDU1xxGhgtJGvui4ERO4pYQaf5hCuBQKMsQpKCkVz0WZs4JpDuMICfNzSPvfEVJf4b89poBXZCVaxwZELST0Ng56zNqAPHf9B8IyXpA4rjTb7FZ1qeqElZTaXmjUJc7OhYo/5Dj+PhmS1VXR6/yCMhpXIhrvhYVAcTamPJOMQOS4ZvmNGE0orYy5IY9R2FzH2k0qJyCUUV1DPcTYEy2oQ+qYh3Fug+WN8B0SXDNJMtay7VRxgQ8YVyKww1dv+m+3ojh7Cbi0OUR6cFxsnobj4c9Rcz7S91AfQtkANbTlLoPzuJ0/WvcNL7MrnutOd/P5hIhP0BvM79Xdz2fFhSp7VuGkyc/UG2xY6XGUz+QtNtoVxglwODD5EfyJzEcH0+mPzrt2u8Jfvli+p40hJR0tV4PajamVfqF6lAsxEh1KkjZtEGdPG/ugFdLUEL/frjv+3Aou/f/saCxVtEC84sBiloc8gcyr7PUBvJg9S3LMpTvk/jU+YMnJgPx+Pm2yt4KGdecflgfss/o+VffMDMhIalhtEF2rJKRiZrtDl6YTRDsfHn3II1td4WMqTnEfZjgGn7pXYrfnFAkIJH41iTRuo4ESYduKKNgx/8uNqRZjI3BaHR8RE/VMnyzX3SNqq4PhekGhDSHZFWbLJ/72A9qP0zPb2xmBhZ/ujA7np2CaOGNTcKE3xGe7BK+8NO2q0rrAusZuVUOGHR4VsTXFTLmbRn3Gzwjy2wYHW/5jITAYDH4l3HqzSxJsU/5tckyyOMM1vuHvTGZa1saTXwPMfZxl6i4RAJMBodXlEipT1o/RCgr6iv72rN7/5MDzKXjp/DeFv8usMiNHcZU9Iw9B2QzbcJKHXwwHb1KWp8c7p1EhtoqvnXCXDoPmP6pFn+QsZGzWlkvkkusfwd6+fRtbWAiTUVTkTQMQZrjp4bhFyoisZC7J7tHkaxkLybblTgq/SNDO3kmQlulfmd8DhZYWHN70P4t7+aRMlNNiEuw9EMnqMWNjZkRGQSHCq7G9ZiYp3NuzFZatkcWfLyrxP4pAwmc/zq67ScHWzk47Fjdakz8/CglZt695pbBxNnefOMu9EX0WcrqRQw46+0s86JI64xmfOj1c6Wpo/1p/XLZmSG6NtadMbNmQvK0L0L5pt4MtznZGwHvCt2/uan39UePQw7c1oCdlJpu8xVoN9fHxoQJMF7S9vb2XCW7M5RN/v6/uJ+cJfUxmN9Q9kh+NxWKzPn8mcRXaSIu7KefaYzDN/S6M7SVfPZBIpDZE2QG8hChPw5jgyRf7ic7OznDqES+BpvKsrNraca7CX78cEt68me/UtrK0XOWLNMZC/ruAPZ+v6g1aUFAQs/OrZ/vCbfz5gfN0tIOYLl+M7aeunh6f1drExp1Sz3mEqXTqKr/n+aHUwHj9tBE9tP71m8ztXu/pn7FPJ3tnGhi9B/w+afbEQFljk9ap4IyA4Iy5Gx3PuGEAST4r0f7XmiMAIzQeUQHb9nXg0hHE5EbJwbL4f8RE3D/a1ZqFpwJrQ3kwlcjr0zNCeZu/3yDi/v++Xe7/+nZcYI1PtRrMecCuDXRBYGBg6+hoymMr0cRedH2gj5N5eFNWHEjgnN4WK0Y44yBd2yLY1M1wxahCS+fJMMhnux/EJdpM/teLMz86aPUbBq0hLRLPV40rJO/wVWhh79cX1foKtFTkVd6K/Iba1/Fw+ZOuf/9+zXahSGPM0H/bdgnrV9czjX84c12aEY5BmuJk6YjBqpClh93Of/sQIibjo4BdPmCsNYQVGKahEyldeg+GSQC0gkEoCGNEG9UsymMqwb5baGcT8BKgX6eY8D+A+xkMTBFS+69YO5TqiYm2I+5ag93uzK09HA310tHShxdr2IT/H1BLBwjlzt06ERYAADMWAABQSwMEFAAICAgAuKBDRAAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK7lAgBQSwcIRczeXRoAAAAYAAAAUEsDBBQACAgIALigQ0QAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vl5bxs3Fv87/RTELFAkW1viNYccKUVToNgAThPUyW6xm90FNUNJrOfqDMeW0/S795GcS5Lt+Ai2wNqWOJx5fPf78XE8/3abpehCVrUq8oVHJthDMo+LROXrhdfo1XHkffviq/laFmu5rARaFVUm9MLjE+4N62A2IdgsVsnCi0O6EqvEP+aSUfgi8lgsmX/MuKBUzPxlglceQttaneTFjyKTdSlieRZvZCZOi1hoy3OjdXkynV5eXk466ZOiWk/X6+VkWyceAs3zeuG1FyfAbmfRJbPkFGMy/fn1qWN/rPJaizyWHjJWNerFV0/mlypPikt0qRK9WXgBjzy0kWq9ATNDHyZTQ1SCraWMtbqQNSwdTa3NOis9SyZy8/yJu0Jpb46HEnWhElktPDzxKQkwn7GIhvbCQ0WlZK5bWtLKnHbc5hdKXjq25spK5HgWQghUrZapXHgrkdZglcpXFXgUFKoamNb6KpVLUXXzQR9yBL9AoD5KwwtC59wAT0KKj2hAjyKCj3wfO2XGkj2kiyK1bDHyZ+jTJ0QxxejIDMQNFIYgcI+wu4eZG6gbuBt8R8Pdcu5IuaPhjoazWwxt54Ol7Y0dUztD2Y6hGB+ZTwAf64E9O6ORncQY8QkRo70dGDJ6E6u/GXg7Ddw0tAPBbiDtw8h8WX8Fj7SIPcgiMpLqEuJmoQcJ00kMWHh3ifRRdg5WsuhQJvVvsPKRzu2EEn/kWpBl/+znQCS7l503uvYeEgP+mOJ/gMAQ75R9V/NuJO14mxu+mFLzaQeH81YhVG8MbZvSWma1UZHNLDghgnwo3iAELPERmcEQmiKmiPiI+zAlEQrMGCJm6pYjhiJk6AhDFoL8CL64rekA+cDL3AxdcSPGkc8QscDFEXgBWfADn1AGFL6PfFhkpBMjlgWIBzBhEeKgoIG90EALg3UwB+EUMYKYWUtCRAMUUBQa6CTcIGoQGd2BKUUBRoFZCtgJuOkwE1ZEiBlroArKola9czcyLfuoWD+qvGx067v2fpwlnR91sUeeFPH5yz1nS1Hr7hqIYMsaNka3he3sm0/mqVjKFLqLM5MHCF2I1JS55b8qco26HODu3roS5UbF9ZnUGlbV6BdxIU6FltsfgLruFLS0cZHXb6tCf1+kTZbXCMVFijvl4JqMrulgcZGy0QM+fuCPHgSj6/BauQU8QU0tQX5R1R25SJJXhmLAAXDfmzy9ellJcV4WateM+dR2JXPZxKlKlMj/DrlupBi/oL5JMRjcNSmBH3SKFFVydlVDAaDtP2VVGGCaMAI/LKSM+7MI8uDKPfEpmwRs+PVBs1iYwuWcTIIwYtSPQj7zQdLV9U+CqI2SvOjjI7ayN31dqWR8/ap+WaRJ7whr+/ei1E1l201A+8pY9F2+TqXND7t/QOMWny+L7ZlLDOZ4vbsqYYad/OXa+hwBqlAfDFm349KNlsYo1lNhS4MtBe4yTSX9czKjlsKOSzdaKkhdp1prKOusJLgTo2qLl9jbKRSb9wtv66EmV/rUzaDIVHzemkrcgh+bbCn79NnlSa7leXV/nvPpXn7Nz2WVy7RNZwhlUzS1q85RpkNyvxV6812e/CTXgCtvhYF2Dawd6aByImOVwUJ3vwuBCex7UNXdTeS6kp2Jqe3wnWvtUzzO6YPbltUPVZG9yi/eQdbsqTqfdvbM67hSpclNtIS95lwO+ZeoWsBOlYzXmUoFK2KDmuBIbZwINdzoTVHZJh6gB0ZToNuykrU5/7g4IGADeLg1oPl0+wwt0FNo9NFf0fY/T+mzZ5a7TGUGbT7SNnlXTW7l9IFc2SOECRgqlr8AaA7dSUswhAII+mz1yU46I5GWG2HOGa2zUnElqx33WX6vi2TfqRAzazlASGkYmPwppXSpp9uSQyUwtBU70mcoDA14fQ7nFlcd/SJz8TeVJNLuRi4HnTsOHJM3maxU3JstrF9A06bTt7PsFl8NuTh2Fb7BU+SOniLXe+qufrq7zct9m8n/v835vs3BtTbvgN+XNPnNalVLjbaw0ZlNr7f8en/UqTnOo0y59ioTW3s0AWnLGjoQLc9igLd8eKPh9G53cDj5mvclZg21r12MODozVyu1HaEUAI/6CJC8i6/Xlhu/rdy+TADjIstEnqDctvTvS2jvzprMG7pJgS0OCmLKFglqMhkJZoLrotTojqwwe5IT0LL9bIa4JQdoQAkOeETwjFEcYp8Hn8uaG4CUYj5KHILpw6vl2gDRu+LhrptPi8tHuLnJ9b393K45cDShISPg6e7vgX5uNywztC3an+Tn/U184b2TW03bffzrX5tCP39jcq7JMnmC4OfNf39zt9E3KIePm/wO231/2yZp/+jrvxD8/L31Z8fk/ed5uAAMTOy3O2LtRg5OQtrbVf5BIbkJMe/ZQtRaVPqtaeyRwTY8iXDgk5BgznBEaOBwFU/CADMaEA41G3LKIQE+9lvc5wNEdgJk2q1F77mnp+Kd/Plfq38/67334YMNgjggEiOi5x9+bUQC5u8TLQ855QdE+ZjIMvpgIvPbO6kgQyGW4KRU/n6POJI/NY6qtnbtt/X2iF4DVKyG4ywcy163/zpwZ3fcvuW5NSm4efVLAapD1qbEbMY4ALlPA0b8cHZTRuxC4yvw7boS6WegcR8TQZX7AaJZcIiGwd7PA+GQ+GyMh4/o0b40GuqfVLzRar1Tb+09UOgfstInA2iZAHdFgO6Y6r2EO3sOjmiJcm2MeZPSUsf/O0iDLiGkeBZhxvyIY9xhWjDj5h87PAwYi3gU3ohpO95YFkUqxXAIjPfzbKi+L9UF3+6AoQsmxLemUXarg2JR2nDYe11y5DY5kMg/SjPb98F0fNC2b73a//G9+ANQSwcIEjnXQF0IAACTHAAAUEsBAhQAFAAICAgAuKBDROXO3ToRFgAAMxYAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX3RodW1ibmFpbC5wbmdQSwECFAAUAAgICAC4oENERczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAABVFgAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIALigQ0QSOddAXQgAAJMcAAAMAAAAAAAAAAAAAAAAALMWAABnZW9nZWJyYS54bWxQSwUGAAAAAAMAAwDCAAAASh8AAAAA" enablerightclick="false" showalgebrainput="false" enableshiftdragzoom="true" showmenubar="false" showtoolbar="false" showtoolbarhelp="true" enablelabeldrags="false" showreseticon="true" />
| |
| |Farbe= #557799 | | |Farbe= #557799 |
| |Rahmen= 0 | | |Rahmen= 0 |