Mathematik 12/Integralrechnung: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
|Titel= Unter- und Obersumme - Video | |Titel= Unter- und Obersumme - Video | ||
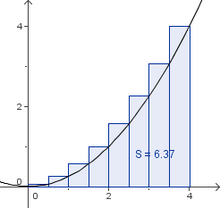
|Inhalt= Eine Möglichkeit ist es, die Fläche mit Hilfe von Streifen zu zerlegen und eine Annährung zu berechnen. Man bildet die Unter- und Obersumme. Eine genaue Erklärung gibts im Video.<br> | |Inhalt= Eine Möglichkeit ist es, die Fläche mit Hilfe von Streifen zu zerlegen und eine Annährung zu berechnen. Man bildet die Unter- und Obersumme. Eine genaue Erklärung gibts im Video.<br> | ||
{{#ev:youtube|pDHujnO9nvQ| | {{#ev:youtube|pDHujnO9nvQ|250px}} | ||
|Farbe= #557799 | |Farbe= #557799 | ||
|Rahmen= 0 | |Rahmen= 0 | ||
| Zeile 51: | Zeile 51: | ||
<ggb_applet id="dguq3rpq" width="400" height="310" /> | <ggb_applet id="dguq3rpq" width="400" height="310" /> | ||
Falls das Applet im Wiki nicht angezeigt wird, klicke hier: [https://www.geogebra.org/m/dguq3rpq Link zum Applet] | Falls das Applet im Wiki nicht korrekt angezeigt wird, klicke hier: [https://www.geogebra.org/m/dguq3rpq Link zum Applet] | ||
{{Lösung versteckt|1= Je höher die Anzahl der Teilintervalle, desto besser ist die Flächenabschätzung. Geht die Anzahl gegen unendlich nähern sich die beiden Werte immer weiter an und haben einen gemeinsamen Grenzwert. | {{Lösung versteckt|1= Je höher die Anzahl der Teilintervalle, desto besser ist die Flächenabschätzung. Geht die Anzahl gegen unendlich nähern sich die beiden Werte immer weiter an und haben einen gemeinsamen Grenzwert. | ||
Aktuelle Version vom 16. September 2021, 20:06 Uhr