6a 2020 21/Mathematik/Übung Flächeninhalt Mix: Unterschied zwischen den Versionen

Aus RMG-Wiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(13 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Box|1=Achtung|2= Heute macht es Klick!! Pass gut auf, dann klappt es. |3=Unterrichtsidee }}
{{Box|1=Achtung|2= Heute macht es Klick!! Pass gut auf, dann klappt es. <br>
Suche dir im Menü aus, was du noch üben musst und lege los. <br>
Denke an die Abgabe. |3=Unterrichtsidee }}


=== 1) Höhen einzeichnen im Dreieck===
=== 1) Höhen einzeichnen im Dreieck===
Zeile 10: Zeile 12:
<ggb_applet id="bV8nkJwc" width="800" height="700" border="888888" />
<ggb_applet id="bV8nkJwc" width="800" height="700" border="888888" />
|3=Arbeitsmethode}}
|3=Arbeitsmethode}}
{{Box|Video|Hier gibts das auch nochmal im Video:
{{#ev:youtube|watch?v=nRJnWvPuuuQ|400|center}}
| Hervorhebung1}}


{{Box|1=Abgabe|2=
{{Box|1=Abgabe|2=
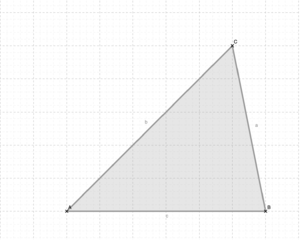
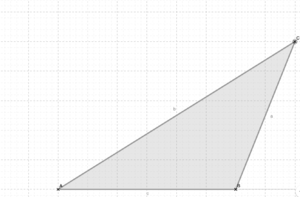
Zeichne nun folgende Dreiecke in dein Heft und trage jeweils die Höhe von c mit Farbe ein. <br>
Zeichne nun folgende Dreiecke in dein Heft und trage jeweils die Höhe von c mit Farbe ein. <br>
Zähle zum Zeichnen die Kästchen ab. <br>
[[Datei:Bildschirmfoto 2021-03-08 um 22.39.54.png|300px]]
[[Datei:Bildschirmfoto 2021-03-08 um 22.39.54.png|300px]]
[[Datei:Dreieck2.png|300px]]
[[Datei:Dreieck2.png|300px]]
Zeile 33: Zeile 40:




=== 3) Dreieck Flächenformel ===
{{Box|1= Flächeninhalt Trapez|2= Hier kannst du testen, ob du die Berechnung des Flächeninhalts eines Trapezes verstanden hast.
{{LearningApp|app=7235700|width=100%|height=400px}}
|3=Üben}}
{{Box|1=Abgabe|2= Zeichne ein Dreieck mit den Punkten A(1/1), B(5/3) und C(1/7) in ein Koordinatensystem. Berechne den Flächeninhalt.
Lade ein Bild davon im Schulmanager im Modul Lernen hoch|3=Download}}


=== 3) Trapez Formel ===
=== 4) Trapez Flächenformel ===




{{Box|1= Flächeninhalt Trapez|2= Hier kannst du testen, ob du die Berechnung des Flächeninhalts eines Trapezes verstanden hast. Für mindestens drei Trapeze solltest du dies schon testen! <br> Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite, dann sollte es normalerweise klappen...Oder klicke [https://www.geogebra.org/m/tN8W92Cf hier]
{{Box|1= Flächeninhalt Trapez|2= Hier kannst du testen, ob du die Berechnung des Flächeninhalts eines Trapezes verstanden hast. Für mindestens drei Trapeze solltest du dies schon testen! <br> Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite, dann sollte es normalerweise klappen...Oder klicke [https://www.geogebra.org/m/tN8W92Cf hier]
<ggb_applet id="tN8W92Cf" width="900" height="500" />
<ggb_applet id="tN8W92Cf" width="900" height="500" />
<br>
<br>
<br>
<br>
|3= Unterrichtsidee}}
|3=Arbeitsmethode}}


{{Box|1= Flächeninhalt Trapez 2|2= Hier ist noch ein super Learning App zum üben.
{{LearningApp|app=16252526|width=100%|height=500px}}
|3=Üben}}


=== 4) Umfang oder Flächeninhalt ===
 
 
{{Box|1=Abgabe|2= Zeichne ein Trapez mit den Punkten A(1/1), B(5/0) C (5/8) und C(1/4) in ein Koordinatensystem. Berechne den Flächeninhalt.
Lade ein Bild davon im Schulmanager im Modul Lernen hoch.|3=Download}}
 
=== 5) Umfang oder Flächeninhalt ===
{{Box|1=Aufgabe 1|2= Verwechselst du manchmal Umfang und Flächeninhalt, mache diese Übung hier.
{{Box|1=Aufgabe 1|2= Verwechselst du manchmal Umfang und Flächeninhalt, mache diese Übung hier.
{{LearningApp|app=9173095|width=100%|height=400px}}
{{LearningApp|app=9173095|width=100%|height=400px}}
|3=Arbeitsmethode}}
|3=Arbeitsmethode}}
{{Box|1=Abgabe|2= Schreibe dir in dein Übungsheft, wie du ab jetzt den Umfang und Flächeninhalt unterscheiden willst.
Lade ein Bild davon im Schulmanager im Modul Lernen hoch.|3=Download}}
=== 6) Flächeninhalt zusammengesetzter Figuren ===
{{Box|1=Aufgabe 1|2= Hier kannst du nochmal die Formeln für den Flächeninhalt verschiedener Figuren wiederholen. Eine ist neu, aber wenn du alle anderen kennst, bleibt diese am Ende übrig und du kannst die Learning App lösen.
{{LearningApp|app=10917886|width=100%|height=400px}}
|3=Arbeitsmethode}}
{{Box|1=Aufgabe 2|2=
{{LearningApp|app=16277405|width=100%|height=700px}}
|3=Üben}}
{{Box|1=Aufgabe 3|2=
{{LearningApp|app=16278106|width=100%|height=600px}}
|3=Arbeitsmethode}}
{{Box|1=Abgabe|2= Im Kapitel 6 gibts heute keine Abgabe|3=Download}}

Aktuelle Version vom 9. März 2021, 07:35 Uhr

Achtung

Heute macht es Klick!! Pass gut auf, dann klappt es.
Suche dir im Menü aus, was du noch üben musst und lege los.

Denke an die Abgabe.

1) Höhen einzeichnen im Dreieck

Höhe im Dreieck - 1

Falls du noch Fehler beim Zeichnen von Höhen im Dreieck gemacht hast, kannst du dies mit folgender Übung trainieren.
Die beiden Kreuzchen auf den Geodreieck ermöglichen es dir das Geodreieck zu drehen und zu verschieben.
Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite, dann sollte es normalerweise klappen... Falls nicht, klicke hier

GeoGebra


Höhe im Dreieck - 2

Bewege die Eckpunkte im Dreieck und schau dir genau an, was mit den Höhen passiert. Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite, dann sollte es normalerweise klappen... Falls nicht, klicke hier

GeoGebra


Video

Hier gibts das auch nochmal im Video:

EmbedVideo fehlt ein anzugebender Parameter.


Abgabe

Zeichne nun folgende Dreiecke in dein Heft und trage jeweils die Höhe von c mit Farbe ein.
Zähle zum Zeichnen die Kästchen ab.
Bildschirmfoto 2021-03-08 um 22.39.54.png Dreieck2.png Dreieck 3.png

Lade ein Bild davon im Schulmanager im Modul Lernen hoch

2) Höhen einzeichnen im Parallelogramm

Einzeichnen der Höhen - 1:
Schau dir die beiden Videos an und achte auf die Unterschiede:
EmbedVideo fehlt ein anzugebender Parameter.

EmbedVideo fehlt ein anzugebender Parameter.


Höhe Parallelogramm - 2

Bewege die Eckpunkte im Parallelogramm und schau dir genau an, was mit den Höhen passiert. Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite, dann sollte es normalerweise klappen... Falls nicht, klicke hier

GeoGebra


Abgabe

Zeichne ein Parallelogramm in dem die Höhe innerhalb liegt und eines in dem die Höhe außerhalb liegt. Markiere die Höhen mit Farbe.

Lade ein Bild davon im Schulmanager im Modul Lernen hoch


3) Dreieck Flächenformel

Flächeninhalt Trapez

Hier kannst du testen, ob du die Berechnung des Flächeninhalts eines Trapezes verstanden hast.


Abgabe

Zeichne ein Dreieck mit den Punkten A(1/1), B(5/3) und C(1/7) in ein Koordinatensystem. Berechne den Flächeninhalt.

Lade ein Bild davon im Schulmanager im Modul Lernen hoch

4) Trapez Flächenformel

Flächeninhalt Trapez

Hier kannst du testen, ob du die Berechnung des Flächeninhalts eines Trapezes verstanden hast. Für mindestens drei Trapeze solltest du dies schon testen!
Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite, dann sollte es normalerweise klappen...Oder klicke hier

GeoGebra




Flächeninhalt Trapez 2

Hier ist noch ein super Learning App zum üben.



Abgabe

Zeichne ein Trapez mit den Punkten A(1/1), B(5/0) C (5/8) und C(1/4) in ein Koordinatensystem. Berechne den Flächeninhalt.

Lade ein Bild davon im Schulmanager im Modul Lernen hoch.

5) Umfang oder Flächeninhalt

Aufgabe 1

Verwechselst du manchmal Umfang und Flächeninhalt, mache diese Übung hier.


Abgabe

Schreibe dir in dein Übungsheft, wie du ab jetzt den Umfang und Flächeninhalt unterscheiden willst.

Lade ein Bild davon im Schulmanager im Modul Lernen hoch.

6) Flächeninhalt zusammengesetzter Figuren

Aufgabe 1

Hier kannst du nochmal die Formeln für den Flächeninhalt verschiedener Figuren wiederholen. Eine ist neu, aber wenn du alle anderen kennst, bleibt diese am Ende übrig und du kannst die Learning App lösen.


Aufgabe 2


Aufgabe 3


Abgabe
Im Kapitel 6 gibts heute keine Abgabe
Abgerufen von „https://rmgwiki.zum.de/index.php?title=6a_2020_21/Mathematik/Übung_Flächeninhalt_Mix&oldid=40373“