6a 2020 21/Mathematik/Flächeninhalt Dreieck: Unterschied zwischen den Versionen

Aus RMG-Wiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 2: Zeile 2:
Heute wollen wir lernen, wie man den Flächeninhalt eines Dreiecks berechnet. <br>
Heute wollen wir lernen, wie man den Flächeninhalt eines Dreiecks berechnet. <br>
Leg dein Merkheft, Geodreieck, Bleistift und Füller bereit. <br>
Leg dein Merkheft, Geodreieck, Bleistift und Füller bereit. <br>
Los gehts mit einem Video.  
'''Los gehts mit einem [https://edpuzzle.com/media/6033f9550f22a94259ea94fa Video.] '''
|3=Hervorhebung1}}
|3=Hervorhebung1}}


Zeile 11: Zeile 11:
Bearbeite im Buch S.135/4<br>
Bearbeite im Buch S.135/4<br>
<br>
<br>
Korrigiere die Lösung. Solltest du etwas anderes haben, komme in die Konferenz und stelle Fragen.
Korrigiere die Lösung. Solltest du etwas anderes haben, komme in die Konferenz und stelle Fragen. <br>
'''ACHTUNG LÖSUNG JETZT NEU UND RICHTIG'''
{{Lösung versteckt|1=
{{Lösung versteckt|1=
a) A=9•4=36 <br>
a) A=<math>\tfrac{1}{2}</math>•9•4=18<br>
b) A=6•4=24 hier ist die eine Seite auch gleichzeitig eine Höhe. <br>
b) A=<math>\tfrac{1}{2}</math>•6•4=12 hier ist die eine Seite auch gleichzeitig eine Höhe. <br>
c) A=3•3=9 <br>
c) A=<math>\tfrac{1}{2}</math>•3•3=4,5 <br>
d) A=3,5•2,7=9,45 Du musst hier 3,5 wählen, das ist die Seitenlänge. Die 1 ist egal. |2=Lösung Aufdecken|3=Verbergen}}
d) A=<math>\tfrac{1}{2}</math>•3,5•2,7=4,725 Du musst hier 3,5 wählen, das ist die Seitenlänge. Die 1 ist egal. |2=Lösung Aufdecken|3=Verbergen}}
|3=Üben}}
|3=Üben}}


Zeile 24: Zeile 25:
* Gehe auf das [https://www.geogebra.org/m/KDQztEtx Applet 1]. Führe die Drehungen aus und schau dir an, weshalb die Linien "Höhe" heißt.
* Gehe auf das [https://www.geogebra.org/m/KDQztEtx Applet 1]. Führe die Drehungen aus und schau dir an, weshalb die Linien "Höhe" heißt.
* Gehe nun auf das [https://www.geogebra.org/m/bV8nkJwc Applet 2]. Verschiebe hier die Eckpunkte und beachte genau, was mit den Höhen passiert.  
* Gehe nun auf das [https://www.geogebra.org/m/bV8nkJwc Applet 2]. Verschiebe hier die Eckpunkte und beachte genau, was mit den Höhen passiert.  
* Übe nun [https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/messen/dreieckshoehen/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/messen/dreieckshoehen/dreieckshoehen_online.html hier das Einzeichnen von Höhen] bis du es sicher kannst. (Mindestens 2 mal)
* Übe nun [https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/messen/dreieckshoehen/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/messen/dreieckshoehen/dreieckshoehen_online.html hier das Einzeichnen von Höhen] bis du es sicher kannst. (Mindestens 2 mal. Du musst diese Seite nicht lesen, nur das Applet nutzen)
* Brauchst du noch Tipps. Hier findest du ein [https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/messen/dreieckshoehen/dreieckshoehen_600x800.jpg  Merkblatt zum Einzeichnen von Höhen] oder ein Video <br>
* Brauchst du noch Tipps. Hier findest du ein [https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/messen/dreieckshoehen/dreieckshoehen_600x800.jpg  Merkblatt zum Einzeichnen von Höhen] oder ein Video <br>
{{#ev:youtube|SORprVHtA8c}}
{{#ev:youtube|SORprVHtA8c}}
Zeile 33: Zeile 34:
Bearbeite S.135/5
Bearbeite S.135/5
{{Lösung versteckt|1=  
{{Lösung versteckt|1=  
Die Seite <math>\overline{PQ}</math> hat die Länge 4,1cm und die dazugehörige Höhe ist 2,3cm lang. Der Flächeninhalt beträgt A=4,1cm•2,3cm=4,715cm² <br>
Die Seite <math>\overline{PQ}</math> hat die Länge 4,1cm und die dazugehörige Höhe ist 2,3cm lang. Der Flächeninhalt beträgt A=<math>\tfrac{1}{2}</math>4,1cm•2,3cm=4,715cm² <br>
<br>
<br>
Die Seite <math>\overline{QR}</math> hat die Länge 2,5cm und die dazugehörige Höhe ist 3,7cm lang. Der Flächeninhalt beträgt A=4,625cm² <br>
Die Seite <math>\overline{QR}</math> hat die Länge 2,5cm und die dazugehörige Höhe ist 3,7cm lang. Der Flächeninhalt beträgt A=4,625cm² <br>
Zeile 42: Zeile 43:
|2=Lösung Aufdecken|3=Verbergen}}
|2=Lösung Aufdecken|3=Verbergen}}
|3=Üben}}
|3=Üben}}
===TEIL 2 ÜBUNGEN ===
{{Box|1=Info|2=Heute üben wir. Verbessere dabei immer gewissenhaft. Schreibe mir eine Nachricht, wenn du eine Übung nicht lösen kannst.
|3=Kurzinfo}}
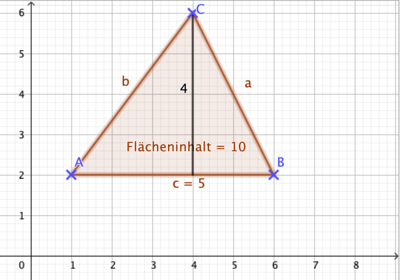
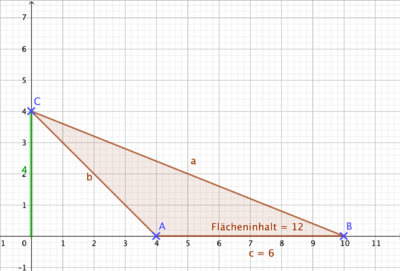
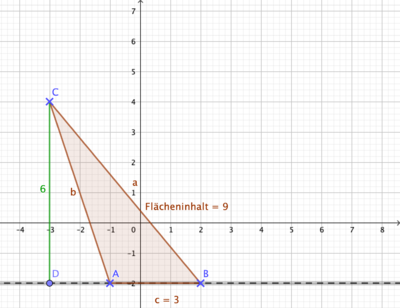
{{Box|1=Übung 1 - Dreiecke im Koordinatensystem|2=
Du kannst hier die Höhen und Grundseiten leicht ablesen.
{{LearningApp|app=7235700|width=100%|height=600px}}
|3= Üben}}
{{Box|1=Übung 2 - Dreiecke im Koordinatensystem Teil 2|2=
Spitze deinen Bleistift, denn jetzt zeichnen wir Koordinatensysteme. Schau dir immer zuerst die Koordinaten an und überlege, wie groß das Koordinatensystem sein muss. <br>
S.136/8a,c,d
{{Lösung versteckt|1=[[Datei:136-8a.png|400px]]
|2=8a Aufdecken|3=Verbergen}}
{{Lösung versteckt|1=[[Datei:136-8c.png|400px]]]
|2=8c Aufdecken|3=Verbergen}}
{{Lösung versteckt|1=[[Datei:136-8d.png|400px]]
|2=8d Aufdecken|3=Verbergen}}
|3=Arbeitsmethode}}
{{Box|1=Übung 3 - Schätzen und Berechnen|2=
Bearbeite S.136/7a und 7b! Lies genau die Aufgabenstellung - du musst hier mehrere Dinge erledigen.
{{Lösung versteckt|1=
# Schätzung: Das Dreieck 2 hat den größten Flächeninhalt, dann (4) dann (1) dann (3). Dies kann man durch Abzählen der Kästchen abschätzen.
# Berechnung:
* Bei (1)  A=<math>\tfrac{1}{2}</math>•2,5cm•2cm=2,5cm² <br>
* Bei (2) A=3,25cm²
* Bei (3) A=1,5cm²
* Bei (4) A=2,75cm²
# Teilaufgabe b) --> Umfang
* Bei (1) ungefähr 7,2cm
* Bei (2) ungefähr 8,9cm
* Bei (3) ungefähr 7,6cm
* Bei (4) ungefähr 8cm
|2=Lösung Aufdecken|3=Verbergen}}
|3=Üben}}
{{Box|1=Übung 4|2=
Löse S.135/3 und S.136/9 schreibe auf, was dir auffällt.
|3=Arbeitsmethode}}

Aktuelle Version vom 23. Februar 2021, 19:37 Uhr

Video

Heute wollen wir lernen, wie man den Flächeninhalt eines Dreiecks berechnet.
Leg dein Merkheft, Geodreieck, Bleistift und Füller bereit.

Los gehts mit einem Video.


Info
Bearbeite nun 3 Übungen.


Übung 1

Weiter gehts mit Übungen. Nimm dein Übungsheft.
Bearbeite im Buch S.135/4

Korrigiere die Lösung. Solltest du etwas anderes haben, komme in die Konferenz und stelle Fragen.
ACHTUNG LÖSUNG JETZT NEU UND RICHTIG


Übung 2

Wir üben nun das Einzeichnen von Höhen.

  • Gehe auf das Applet 1. Führe die Drehungen aus und schau dir an, weshalb die Linien "Höhe" heißt.
  • Gehe nun auf das Applet 2. Verschiebe hier die Eckpunkte und beachte genau, was mit den Höhen passiert.
  • Übe nun hier das Einzeichnen von Höhen bis du es sicher kannst. (Mindestens 2 mal. Du musst diese Seite nicht lesen, nur das Applet nutzen)
  • Brauchst du noch Tipps. Hier findest du ein Merkblatt zum Einzeichnen von Höhen oder ein Video
Höhen im Dreieck, Wie zeichnet man eine Höhe?, Höhenschnittpunkt
Video laden
YouTube


Übung 3

Bearbeite S.135/5

TEIL 2 ÜBUNGEN

Info
Heute üben wir. Verbessere dabei immer gewissenhaft. Schreibe mir eine Nachricht, wenn du eine Übung nicht lösen kannst.


Übung 1 - Dreiecke im Koordinatensystem

Du kannst hier die Höhen und Grundseiten leicht ablesen.


Übung 2 - Dreiecke im Koordinatensystem Teil 2

Spitze deinen Bleistift, denn jetzt zeichnen wir Koordinatensysteme. Schau dir immer zuerst die Koordinaten an und überlege, wie groß das Koordinatensystem sein muss.
S.136/8a,c,d


Übung 3 - Schätzen und Berechnen

Bearbeite S.136/7a und 7b! Lies genau die Aufgabenstellung - du musst hier mehrere Dinge erledigen.


Übung 4
Löse S.135/3 und S.136/9 schreibe auf, was dir auffällt.
Abgerufen von „https://rmgwiki.zum.de/index.php?title=6a_2020_21/Mathematik/Flächeninhalt_Dreieck&oldid=37401“