6a 2020 21/Mathematik/Flächeninhalt Dreieck: Unterschied zwischen den Versionen
Aus RMG-Wiki
< 6a 2020 21 | Mathematik
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (11 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Heute wollen wir lernen, wie man den Flächeninhalt eines Dreiecks berechnet. <br> | Heute wollen wir lernen, wie man den Flächeninhalt eines Dreiecks berechnet. <br> | ||
Leg dein Merkheft, Geodreieck, Bleistift und Füller bereit. <br> | Leg dein Merkheft, Geodreieck, Bleistift und Füller bereit. <br> | ||
Los gehts mit einem Video. | '''Los gehts mit einem [https://edpuzzle.com/media/6033f9550f22a94259ea94fa Video.] ''' | ||
|3=Hervorhebung1}} | |3=Hervorhebung1}} | ||
| Zeile 11: | Zeile 11: | ||
Bearbeite im Buch S.135/4<br> | Bearbeite im Buch S.135/4<br> | ||
<br> | <br> | ||
Korrigiere die Lösung. Solltest du etwas anderes haben, komme in die Konferenz und stelle Fragen. | Korrigiere die Lösung. Solltest du etwas anderes haben, komme in die Konferenz und stelle Fragen. <br> | ||
'''ACHTUNG LÖSUNG JETZT NEU UND RICHTIG''' | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
a) A= | a) A=<math>\tfrac{1}{2}</math>•9•4=18<br> | ||
b) A= | b) A=<math>\tfrac{1}{2}</math>•6•4=12 hier ist die eine Seite auch gleichzeitig eine Höhe. <br> | ||
c) A= | c) A=<math>\tfrac{1}{2}</math>•3•3=4,5 <br> | ||
d) A= | d) A=<math>\tfrac{1}{2}</math>•3,5•2,7=4,725 Du musst hier 3,5 wählen, das ist die Seitenlänge. Die 1 ist egal. |2=Lösung Aufdecken|3=Verbergen}} | ||
|3=Üben}} | |3=Üben}} | ||
{{Box|1=Übung 2|2= | {{Box|1=Übung 2|2= | ||
< | Wir üben nun das Einzeichnen von Höhen. <br> | ||
* Gehe auf das [https://www.geogebra.org/m/KDQztEtx Applet 1]. Führe die Drehungen aus und schau dir an, weshalb die Linien "Höhe" heißt. | |||
* Gehe nun auf das [https://www.geogebra.org/m/bV8nkJwc Applet 2]. Verschiebe hier die Eckpunkte und beachte genau, was mit den Höhen passiert. | |||
* Übe nun [https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/messen/dreieckshoehen/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/messen/dreieckshoehen/dreieckshoehen_online.html hier das Einzeichnen von Höhen] bis du es sicher kannst. (Mindestens 2 mal. Du musst diese Seite nicht lesen, nur das Applet nutzen) | |||
* Brauchst du noch Tipps. Hier findest du ein [https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/sekundarstufe1/messen/dreieckshoehen/dreieckshoehen_600x800.jpg Merkblatt zum Einzeichnen von Höhen] oder ein Video <br> | |||
{{#ev:youtube|SORprVHtA8c}} | |||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
| Zeile 27: | Zeile 34: | ||
Bearbeite S.135/5 | Bearbeite S.135/5 | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Die Seite <math>\overline{PQ}</math> hat die Länge 4,1cm und die dazugehörige Höhe ist 2,3cm lang. Der Flächeninhalt beträgt A=4,1cm•2,3cm=4,715cm² <br> | Die Seite <math>\overline{PQ}</math> hat die Länge 4,1cm und die dazugehörige Höhe ist 2,3cm lang. Der Flächeninhalt beträgt A=<math>\tfrac{1}{2}</math>4,1cm•2,3cm=4,715cm² <br> | ||
<br> | <br> | ||
Die Seite <math>\overline{QR}</math> hat die Länge 2,5cm und die dazugehörige Höhe ist 3,7cm lang. Der Flächeninhalt beträgt A=4,625cm² <br> | Die Seite <math>\overline{QR}</math> hat die Länge 2,5cm und die dazugehörige Höhe ist 3,7cm lang. Der Flächeninhalt beträgt A=4,625cm² <br> | ||
| Zeile 35: | Zeile 42: | ||
Die Unterschiede beim Flächeninhalt entstehen durch Messungenauigkeiten (Rundungen). Weichen deine Messungen um einen Millimeter ab, ist das kein Problem. Hast du größere Abweichungen oder ganz andere Werte, mache ein Bild und schicke es mir. Dann können wir schauen, wo der Fehler liegt. | Die Unterschiede beim Flächeninhalt entstehen durch Messungenauigkeiten (Rundungen). Weichen deine Messungen um einen Millimeter ab, ist das kein Problem. Hast du größere Abweichungen oder ganz andere Werte, mache ein Bild und schicke es mir. Dann können wir schauen, wo der Fehler liegt. | ||
|2=Lösung Aufdecken|3=Verbergen}} | |2=Lösung Aufdecken|3=Verbergen}} | ||
|3=Üben}} | |||
===TEIL 2 ÜBUNGEN === | |||
{{Box|1=Info|2=Heute üben wir. Verbessere dabei immer gewissenhaft. Schreibe mir eine Nachricht, wenn du eine Übung nicht lösen kannst. | |||
|3=Kurzinfo}} | |||
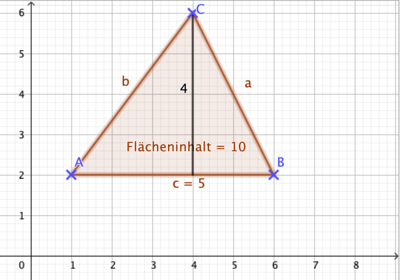
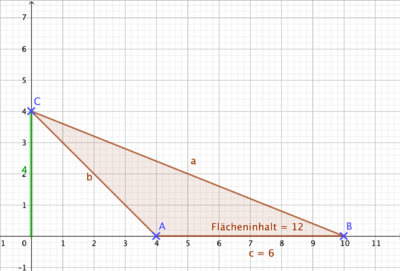
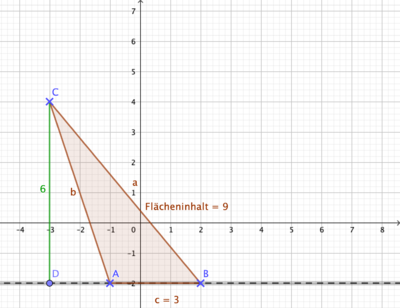
{{Box|1=Übung 1 - Dreiecke im Koordinatensystem|2= | |||
Du kannst hier die Höhen und Grundseiten leicht ablesen. | |||
{{LearningApp|app=7235700|width=100%|height=600px}} | |||
|3= Üben}} | |||
{{Box|1=Übung 2 - Dreiecke im Koordinatensystem Teil 2|2= | |||
Spitze deinen Bleistift, denn jetzt zeichnen wir Koordinatensysteme. Schau dir immer zuerst die Koordinaten an und überlege, wie groß das Koordinatensystem sein muss. <br> | |||
S.136/8a,c,d | |||
{{Lösung versteckt|1=[[Datei:136-8a.png|400px]] | |||
|2=8a Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:136-8c.png|400px]]] | |||
|2=8c Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:136-8d.png|400px]] | |||
|2=8d Aufdecken|3=Verbergen}} | |||
|3=Arbeitsmethode}} | |||
{{Box|1=Übung 3 - Schätzen und Berechnen|2= | |||
Bearbeite S.136/7a und 7b! Lies genau die Aufgabenstellung - du musst hier mehrere Dinge erledigen. | |||
{{Lösung versteckt|1= | |||
# Schätzung: Das Dreieck 2 hat den größten Flächeninhalt, dann (4) dann (1) dann (3). Dies kann man durch Abzählen der Kästchen abschätzen. | |||
# Berechnung: | |||
* Bei (1) A=<math>\tfrac{1}{2}</math>•2,5cm•2cm=2,5cm² <br> | |||
* Bei (2) A=3,25cm² | |||
* Bei (3) A=1,5cm² | |||
* Bei (4) A=2,75cm² | |||
# Teilaufgabe b) --> Umfang | |||
* Bei (1) ungefähr 7,2cm | |||
* Bei (2) ungefähr 8,9cm | |||
* Bei (3) ungefähr 7,6cm | |||
* Bei (4) ungefähr 8cm | |||
|2=Lösung Aufdecken|3=Verbergen}} | |||
|3=Üben}} | |||
{{Box|1=Übung 4|2= | |||
Löse S.135/3 und S.136/9 schreibe auf, was dir auffällt. | |||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
Aktuelle Version vom 23. Februar 2021, 19:37 Uhr
TEIL 2 ÜBUNGEN