6B Vor Weihnachten: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 37: | Zeile 37: | ||
{{Box|1=Vergleiche das Erweitern mit dem Vervielfachen!|2= | {{Box|1=Vergleiche das Erweitern mit dem Vervielfachen!|2= | ||
Bearbeite | Bearbeite im Übungsheft und vergleiche dann deine Lösung. <br> | ||
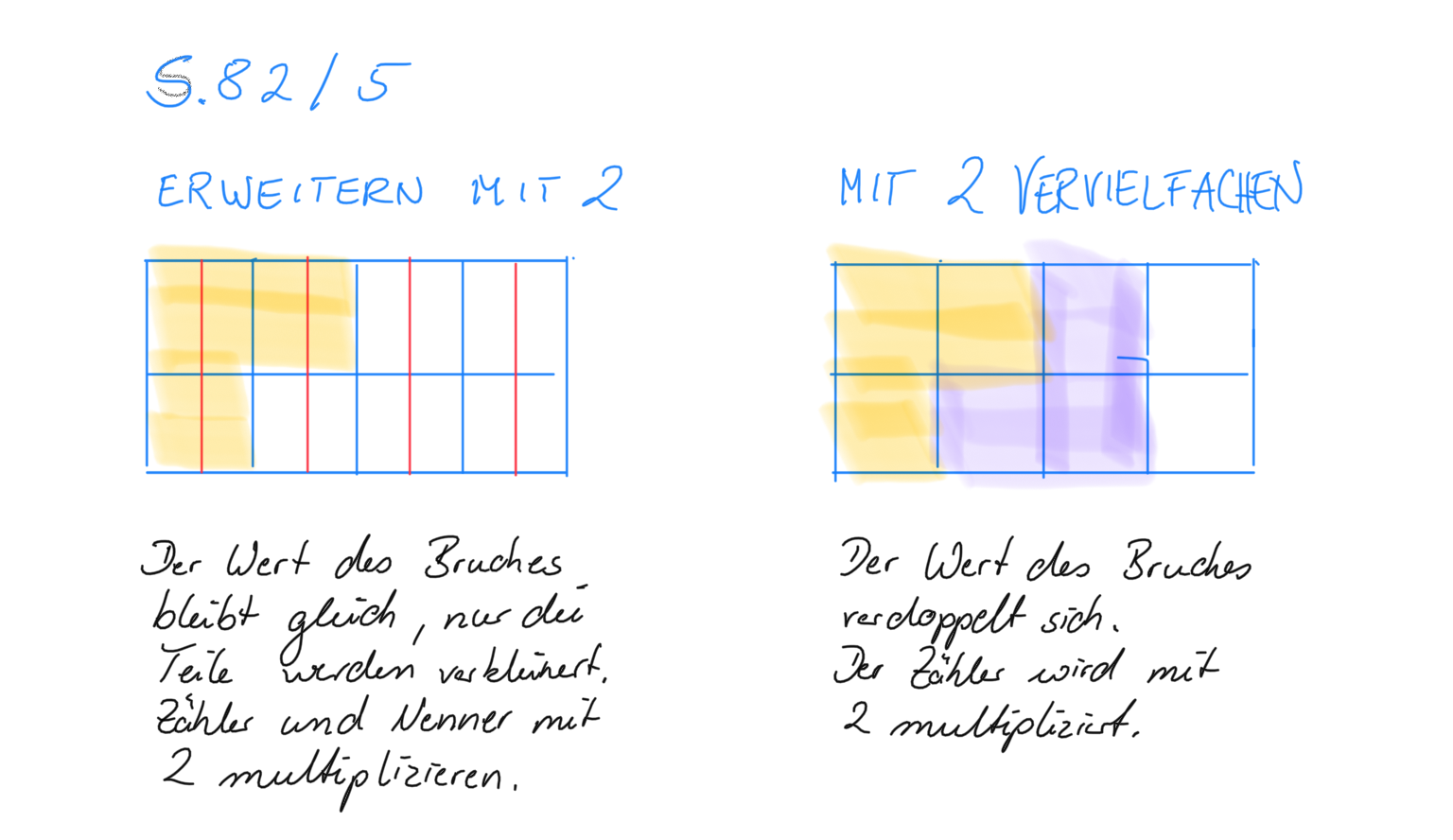
S.82/5 | |||
{{Lösung versteckt|1=[[Datei:PNG-Bild 2.png|midi]]|2=Aufdecken|3=Verbergen}} | {{Lösung versteckt|1=[[Datei:PNG-Bild 2.png|midi]]|2=Aufdecken|3=Verbergen}} | ||
|3=Üben}} | |3=Üben}} | ||
| Zeile 59: | Zeile 60: | ||
<math> x \cdot {2 \over 5}= {2 \over 10}</math> (!x = 1) (x= 2) (!x=4) | <math> x \cdot {2 \over 5}= {2 \over 10}</math> (!x = 1) (x= 2) (!x=4) | ||
<math> x \cdot {1 \over 4}= 1 {3 \over 4}</math> (!x = | <math> x \cdot {1 \over 4}= 1 {3 \over 4}</math> (!x = 2) (x= 7) (!x=3) | ||
</div> | </div> | ||
|3=Unterrichtsidee}} | |3=Unterrichtsidee}} | ||
{{Box|1=Jetzt bist du nochmal dran!|2= | {{Box|1=Jetzt bist du nochmal dran!|2= | ||
Bearbeite im Übungsheft und vergleiche dann deine Lösung. | |||
S.82/9 | S.82/9 | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||