M6 4.2 Flächeninhalt eines Dreiecks
Wir haben gerade gesehen, dass man die Formel für den Flächeninhalt mit Hilfe des Parallelogramms herleiten kann. Es geht aber auch mit Hilfe des Rechtecks.

4. 2 Flächeninhalt eines Dreiecks
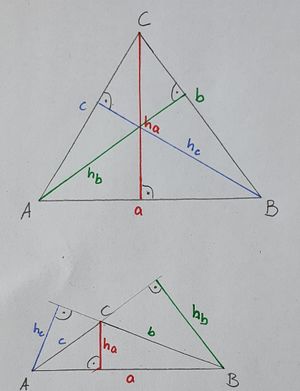
Zeichne zwei Dreieck (wie im Buch) und alle drei Höhen, wie im vorgehenden Erklärvideo gesehen.
Ist noch etwas unklar, dann schaue das Video nochmal!
Vervollständige deinen Hefteintrag mit dem folgenden Merksatz!
Flächeninhalt eines Dreiecks
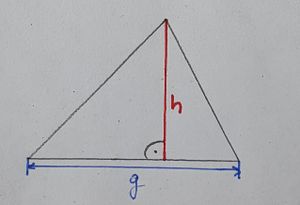
Der Flächeninhalt A eines Dreiecks ist gleich die Hälfte des Produkts aus der Seitenlänge und der zugehörigen Höhe.
Allgemein gilt: , der Flächeninhalt ist die Hälfte des Produkts aus einer Seite (Grundseite g) und zugehöriger Höhe (h).
Anmerkung: Um klar zu machen, welche Höhe und welche Grunseite gemeint ist schreibt man auch oft:
Ein kleiner Test zum Verständnis des Flächeninhalts des Dreiecks... Bearbeite B. S. 135/ 4a), b) und d)! Überlege dir jeweils genau, was ist die Seite des Dreiecks, wie lang ist diese und was die zugehörige Höhe. Vergleiche im Anschluss bitte deine Lösung mit meinem Lösungsvorschlag.
Erinnerung: Notiere dir stets, was gegeben ist und schreibe auch immer die Formel auf, die du zur Bearbeitung der Aufgabe verwendest.
Lösung der Aufgaben:
a)
g = 9 cm und h = 4 cm
b)
g = 6 cm und h = 4 cm oder aber auch g = 4 cm und h = 6 cm, denn zwei Seiten des Dreiecks stehen aufeinander senkrecht. Damit ist die eine Seite die Höhe zu der Seite, auf der sie senkrecht steht oder eben umgekehrt...
d)
ACHTUNG: g = 3,5 cm und h = 2,7 cm
Anmerkung: "