M5 V Flächeninhalt

<5b 2019 20

1 Flächenvergleich

Merke

Zerlegt man eine Fläche so, dass sie mit einer anderen Fläche übereinstimmt, so haben die beiden Flächen denselben Flächeninhalt.

Üben

1. Zeichne zwei Flächen mit dem Flächeninhalt 15cm² in dein Übungsheft.
2. Miss bei beiden Flächen den Umfang und notiere ihn daneben: U=___.

2 Einheiten für Flächeninhalte

Übung ins Übungsheft

Vorsicht! Hier stehen verschiedene Einheiten. Gib in der in Klammern angegebenen Einheit an. Notiere in dein Heft und schicke mir ein Bild.

1. 12 cm² (mm²)
2. 2300 dm² (cm²)
3. 400 m² (cm²)
4. 3,4 ha (a)
5. 340 a (ha)
6. 3,4 km (m)
7. 3,45 cm² (mm²)
8. 0,3 m² (dm²)
9. 3dm 4mm (cm)
10. 1m² 34dm² (dm²)
11. 1m² 34dm² (m²)

Flächeninhalt und Umfang von Rechtecken

Kästchen zählen

Ihr kennt bereits die verschiedenen geometrischen Figuren.

Heute wollen wir uns mit dem Flächeninhalt von geometrischen Figuren beschäftigen.

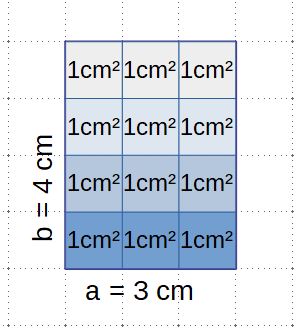
Betrachtet dazu die Zeichnungen und ermittelt, aus wie vielen Kästchen die Rechtecke bestehen.

Rechteck 1: 15 Kästchen; Rechteckt 2: 12 Kästchen; Rechteck 3: 10 Kästchen

Info

Bei einem Rechteck bezeichnet man die Seiten mit a und b.

Zeichnen von 3 Rechtecken

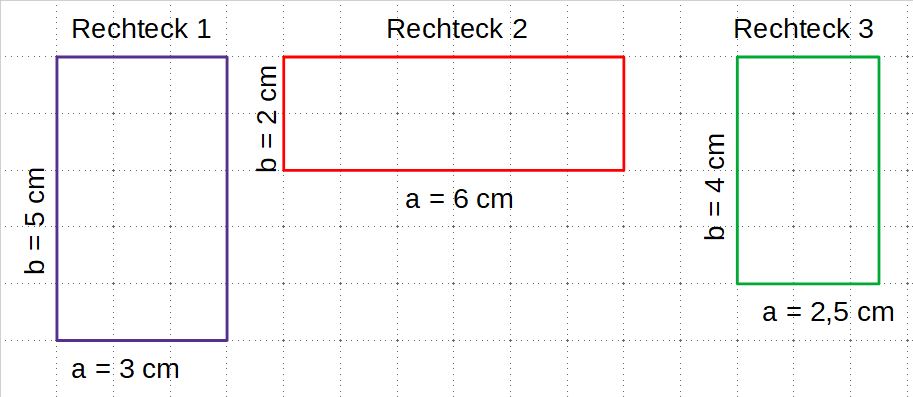
• Zeichne ein Rechteck mit den Maßen a = 3cm; b = 4cm, ein Rechteck mit den Maßen a= 2cm und b = 6cm und das dritte Rechteck hat die Seitenlängen a = 8cm und b = 1,5 cm. Notiere die Seitenlängen am Rechteck.

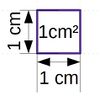
• Aus wie vielen 1cm² bestehen die Rechtecke? (Zur Erinnerung: 1cm² hat die Maße 1cm x 1cm, also 4 Kästchen)

• Notiere, was dir auffällt.

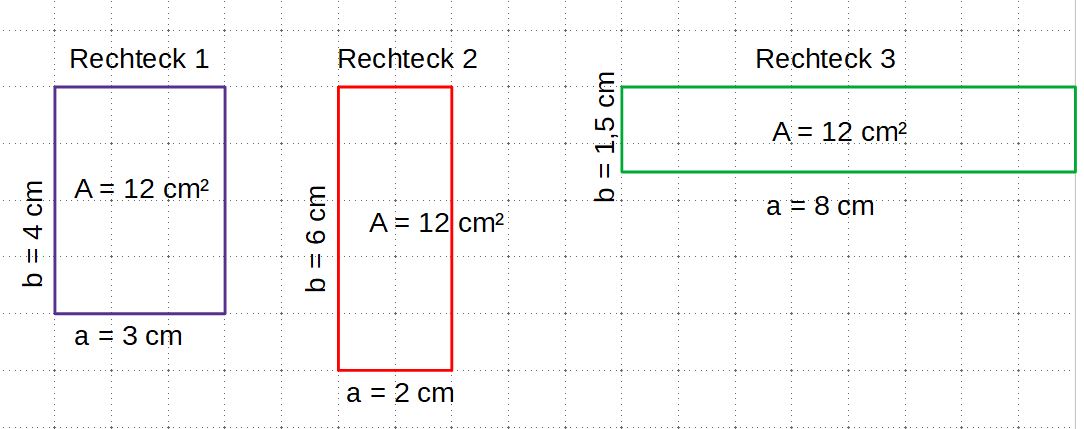
Obwohl die Seitenlängen der Rechtecke unterschiedlich sind, haben alle drei den gleichen Flächeninhalt. Sie bestehen alle aus 12 cm².

Info

Möchte man den Flächeninhalt eines Rechtecks bestimmen, so kann man es erst einmal in gleich große Streifen zerlegen. Dieses Rechteck besteht aus 4 Streifen mit je 3 cm².

Der Flächeninhalt A dieses Rechtecks beträgt also: $A = 4 \cdot 3 cm² = 12 cm^2$

Merke

Flächeninhalt des Rechtecks
Der Flächeninhalt A eines Rechtecks mit den Seitenlängen a und b:

1. Der Flächeninhalt eines Rechtecks ergibt sich aus dem Produkt der Seitenlängen.
2. Es gilt also: $A = a \cdot b$

Wer jetzt noch etwas zum Berechnen von Flächeninhalten sehen möchte, kann sich dieses Video noch anschauen.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Notiere in dein Heft:

Formeln für den Flächeninhalt und den Umfang von Rechtecken.

• Ergänze aus dem Buch S.230 den Merkkasten.
  
• Schreibe auch den Merkkasten zum Umfang S.231 darunter.

Übung 1

1. Berechne nun auch den Flächeninhalt der anderen beiden Rechtecke Seitenlängen a = 8 cm und b = 1,5 cm sowie das Rechteck a = 2 cm und b = 6 cm, die du in dein Heft gezeichnet hast.

Tipp:Wandle bei Kommazahlen beide Seitenlängen in die nächstkleinere Einheit um und rechne dann.

1. Berechne nun auch unter/neben den Rechtecken den Umfang. Was fällt dir auf?

Vorlage:Lösung versteck

Übung 2

Berechne den Flächeninhalt A und den Umfang U der folgenden Rechtecke mit den Seitenlänge. Achte auch auf die Einheiten.

a) a = 4 cm, b = 7 cm

b) a = 4 mm, b = 7 mm

c) a = 5 dm, b = 12 dm

d) a = 23 m, b = 8 m

Achtung

Man kann nur Seitenlängen mit gleicher Einheit miteinander multiplizieren!

Übung 3

Berechne jeweils den Flächeninhalt der Rechtecke in einer geeigneten Einheit.

a) b = 5 cm, c = 70 dm

b) a = 1200 mm, b = 9 dm

c) c = 5 km, d = 3000 m

d) a = 50 cm, d = 200 mm

e) a = 1200 dm, b = 15 m (Gib hier den Flächeninhalt in cm² an.)

f) b = 5 m, c= 200 cm (Gib hier den Flächeninhalt in dm² an.)