Das Parallelogramm
Üben
Wiederholung Vierecke
Üben
Wiederholung Flächeninhalt und Umfang
- Für ein Rechteck mit den Seitenlängen a und b gilt:
- Für den Umfang: U = 2•a+2•b= 2•(a+b)
- Für den Flächeninhalt: A = a • b
- Durch geschicktes Zerlegen und Ergänzen kann man den Flächeninhalt zusammengesetzter Flächen berechnen.
Lösung
Hier ist noch die Lösung
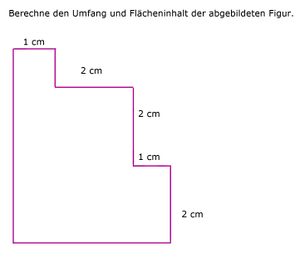
- U=1cm+1cm+2cm+2cm+1cm+2cm+4cm+5cm=18cm
- Zerlegt in 3 Rechtecke:
- A1=1cm·5cm=5cm2
- A2=2cm·4cm=8cm2
- A3=1cm·2cm=2cm2
- A=A1+A2+A3=15cm2
Überlegung
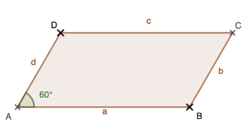
Aus der 5. Klasse kennen wir die Formeln zur Berechnung des Flächeninhalts von Rechtecken. Wir interessieren uns nun dafür, wie man den Flächeninhalt eines Parallelogramms bestimmt. Zunächst verwenden wir ein konkretes Beispiel.
Zeichne ein Parallelogramm ABCD mit der Länge a=10cm und d=5cm sowie α=60°. Wenn du ein buntes Papier hast, gerne darauf
Bestimme den Flächeninhalt. Du kannst die Figur auch zerschneiden.
Wir werden die Lösungen in der nächsten Videokonferenz besprechen.
Höhen im Parallelogramm
Hefteintra
Schreibe eine neue große Überschrift:
4. Flächeninhalt und Volumen
4.1. Flächeninhalt eines Parallelogramms
Schreibe nun alles mit, wenn es mit "Hefteintrag" markiert ist.
Um die Formel für den Flächeninhalt eines Parallelogramms herzuleiten, musst du den Begriff der "Höhe" kennen.
Hefteintrag
Höhen im Parallelogramm
Der Abstand zwischen den parallelen Seiten des Parallelogramms wird als Höhe bezeichnet. Ein Parallelogramm hat zwei Höhen.
Du zeichnest die Höhe, indem du eine Strecke rechtwinklig zu einer Seite zeichnest und diese mit der dazu parallelen Seite verbindest.
Verschiebe im nachfolgenden Applet die Punkte und beobachte die Lage der Höhen. Was fällt dir auf? Notiere es im Heft für die nächste Videokonferenz
Höhen im Parallelogramm zeichnen
Zeichne ein beliebiges Parallelogramm in dein Heft und beschrifte die Seiten a und b. Zeichne nun die Höhen ha und hb.
Falls du Schwierigkeiten damit hast, helfen dir die Bildfolgen im
Original des Lernpfads.