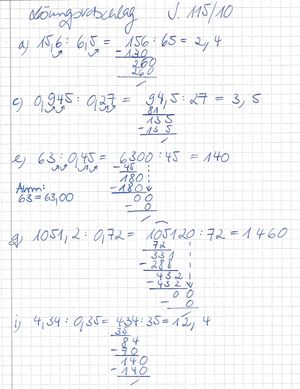6e Lernen zu Hause: Dividieren von Dezimalbrüchen
01.02.2021
Zu Beginn wirst du noch einmal Aufgaben zum Multiplizieren von Dezimalbrüchen bearbeiten. Berechne hierfür im Buch S. 105/ 6i), j), und S. 106/ 17 c), d)!
Nachdem du diese Aufgaben bearbeitet hast, schicke mir bitte deine Lösung im Schulmanager - Modul Lernen. Ich würde sehr gerne einen Blick darauf werfen, wie gut du schon mit dem Multiplizieren von Dezimalbrüchen zurecht kommst. Danke!
Berechne schriftlich!
Sieh dir nun zunächst folgendes Video aufmerksam an! Notiere dir zeitgleich die drei Aufgaben, die im Video berechnet werden auf einem Schmierzettel, damit du diese im Anschluss an das Video noch einmal alleine berechnen kannst...
Nun bist du an der Reihe! Berechne jetzt nochmal alle Aufgaben aus dem Video in deinem Schulheft. Solltest du nicht mehr weiter wissen, schau dir nochmal die entsprechende Stelle im Video dazu an. Versuche aber bitte zunächst die Aufgaben ohne Hilfe zu rechnen.
Notiere bitte noch folgenden Merksatz in dein Heft!
Merke: Division eines Dezimalbruchs durch eine natürliche Zahl
- Dividiere den Dezimalbruch stellenweise durch die natürliche Zahl, so wie du es von der Division einer natürlichen Zahl durch eine natürliche Zahl bereits gewohnt bist.
- Wichtig: Sobald du bei der Berechnung das Komma "überschreitest", setze auch im Ergebnis ein Komma!
- Eventuell ist es nötig, um die Aufgabe komplett berechnen zu können, zum Ende des Rechenvorgangs beim Dezimalbruch noch nicht geschriebene Endnullen zu ergänzen.
Lies dir diesen Merksatz nun noch einmal in Ruhe durch und verinnerliche die Vorgehensweise bei der Division eines Dezimalbruchs durch eine natürliche Zahl bevor es mit Übungen weiter geht!
Kopfrechnen - Schlage das Buch S. 110/ 2 auf, stelle dir einen Timer auf 5 Minuten und versuche in der Zeit so viele Aufgaben wie möglich zu berechnen.
Notiere dir jeweils dein Ergebnis, damit du deine Lösung mit meiner im Anschluss vergleichen kannst.... Ich hoffe du bist schon zurecht gekommen!
Nun bestimmt etwas schwieriger für dich: Berechne B. S. 110/ 5 a), b), c), d), g) und freiwillig e)!
Versuche konzentriert jede Aufgabe zu berechnen, wende dein neu erworbenes Wissen an und versuche ruhig zu bleiben, dann kommst du sicher ans Ziel!
Mit diesen Aufgaben sollst du Rechenroutine bekommen... Bitte bei Teilaufgabe e), falls du diese freiwillig versuchst, nach spätestens 5 Minuten aufhören!
Verbessere bitte deinen Lösungsvorschlag!
Falls dein Ergebnis ein anderes sein sollte, dann vergleiche bitte deine Lösung Schritt für Schritt mit der von mir!
Damit du das Multiplizieren von Dezimalbrüchen nicht so schnell vergisst, kannst du es mit folgenden Aufgaben zum einen wiederholen und zum anderen weiter vertiefen.
Parat haben solltest du hierfür auch das Wissen zu Potenzen und die Rechenvorschrift "von links nach rechts"...
Berechne nun Buch S. 107/ 20 a), b), c) und S. 107/ 22/ a), e), f)!
Tipp: Berechne hier Schritt für Schritt von "links nach rechts"! Vergiss die Zwischenschritte nicht!
a) 1,4·2,6·3 = 3,64·3 = 10,92
b) 4,9·7·1,5 = 34,3·1,5 = 51,45
c) 0,62·0,25·17,8 = 0,155·17,8 = 2,759
a) 1,52 = 1,5·1,5 = 2,25
e) 1,23 = 1,2·1,2·1,2 = 1,44·1,2 = 1,728
f) 2,53 = 2,5·2,5·2,5 = 6,25·2,5 = 15,625
Falls du letzten Donnerstag nicht genug Energie mehr hattest, kannst du ja heute nochmal das Multiplizieren von Dezimalbrüchen üben...nimm dir bitte für Nebenrechnungen einen Stift und dein Heft zur Hand, das Erraten der Lösungen bringt leider nicht sehr viel...
03.02.2021
Berechne zu Beginn im Buch S. 110/ 4 a) b), l) und 5 i)!
Nachdem du diese Aufgaben bearbeitet hast, schicke mir bitte deine Lösung im Schulmanager - Modul Lernen. Ich würde sehr gerne einen Blick darauf werfen, wie gut du schon mit dem Dividieren von Dezimalbrüchen durch eine natürliche Zahl zurecht kommst. Danke!
Die gute Nachricht hierbei ist, dass diese Fähigkeit des Berechnens auf die Division eines Dezimalbruchs durch eine natürliche Zahl zurückzuführen ist. Man schiebt nämlich hier immer das Komma beim Divisor - das ist die 2. Zahl ;-) - so lange nach rechts bis der Divisor eine natürliche Zahl ist. Wichtig: Beim Dividenden - das ist die 1. Zahl ;-) - muss man das Komma um genauso viele Stellen nach rechts schieben, wie auch beim Divisor. Das war' s eigentlich auch schon...
Also keine Angst, dass wird bestimmt gut!
Notiere dir noch die Überschrift Dividieren von Dezimalbrüchen durch Dezimalbrüche in dein Heft und schau dir nun zunächst folgendes Video aufmerksam an, notiere dir hierbei auch die drei Aufgaben aus dem Video auf einem Schmierzettel!
Jetzt bist du an der Reihe! Berechne nun nochmal alleine die drei Aufgaben aus dem Video! Falls du an einer Stelle nicht weiterkommst, schau dir hierzu dann einfach nochmal das Video an. Danke!
Notiere bitte noch folgenden Merksatz in dein Heft!
Merke: Dividieren eines Dezimalbruchs durch einen Dezimalbruch
Man verschiebt bei beiden Zahlen das Komma um gleich viele Stellen nach rechts, bis der Divisor eine natürliche Zahl ist.
Dann dividiert man durch die natürliche Zahl.
Der Wert eines Quotienten ändert sich nicht, wenn man das Komma bei Dividend und Divisor um gleich viele Stellen in dieselbe Richtung verschiebt.
Lies dir diesen Merksatz nun noch einmal in Ruhe durch und verinnerliche die Vorgehensweise bei der Division eines Dezimalbruchs durch einen Dezimalbruch!
Berechne!
a) 4,05 : 2,7
b) 1,875: 3,125
Noch etwas Kopfrechnen - Schlage das Buch S. 114/ 4 auf und berechne nacheinander die Aufgaben im Kopf.
Notiere dir jeweils dein Ergebnis, damit du deine Lösung mit meiner im Anschluss vergleichen kannst.... Morgen kannst du mir ja erzählen, wie gut du zurecht gekommen bist...
e) "50 : 25" = 2; f) "2000 : 2" = 1000; g) "15 : 3" = 5; h) "30 : 6" = 5;
i) "200 : 4" = 50; j) "64: 8" = 8; k) "250 : 2" = 125; l) "1800 : 6" = 300;
04.02.2021
Bearbeite nun noch folgende Arbeitsaufträge nach der Videokonferenz! So kannst du gleich auch testen, ob du alles verstanden hast.
Berechne schriftlich B. S. 115/ 10 a), c), e), g), i)!
Verbessere bitte deinen Lösungsvorschlag!
Falls dein Ergebnis ein anderes sein sollte, vergleiche bitte deine Lösung Schritt für Schritt mit der von mir! Falls dir mein Lösungsvorschlag in der Darstellung zu klein sein sollte, kannst du einfach auf die beiden Rechtecke unten rechts im Bild klicken und es vergrößert sich.
WICHTIG: Vergiss nicht die Lösung der Aufgabenpaare im Schulheft zu berechnen/ zu notieren, nachdem du diese zugeordnet hast!
Die Aufgabenpaare inklusive zugehöriger Lösung:
- 32 : 800 = 0,32 : 8 = 0,04
- 32 : 8 = 3,2 : 0,8 = 4
- 3200 : 8 = 32 : 0,08 = 400
- 30 : 6 = 0,3 : 0,06 = 5
- 300: 6 = 3 : 0,06 = 50
- 96 : 12 = 0,96 : 0,12 = 8
Potenzen und Dezimalbrüche...
Berechne jeweils und ordne das richtige Ergebnis zu. Achte hierbei auf die richtige Anzahl der Nachkommastellen!
Du hast es dir sicher schon gedacht, auch beim Rechnen mit Dezimalzahlen gelten nach wie vor die Rechenregeln "Klammern zuerst", "Potenz vor Punkt vor Strich", "von links nach rechts" und natürlich können Dezimalbrüche auch in Textaufgaben vorkommen...
Berechne die jeweilige Aufgabe im Kopf! Mit diesen Aufgaben kannst du testen, ob du Rechengesetze richtig anwendest und Textaufgaben richtig verstehst... Wenn du magst, kannst du dir hierbei freiwillig die jeweilige Aufgabe inklusive ihrer Lösung kurz ins Schulheft notieren.
Anmerkung: Pickerl = Sticker
Am Montag geht es dann mit Aufgaben zu Dezimalbrüchen weiter. Hab ein schönes Wochenende!