Corona-Arbeitsaufträge (Bio) LUX: Unterschied zwischen den Versionen
Aus RMG-Wiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(AA Bio6 hierhin verschoben) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 251: | Zeile 251: | ||
Diese Einheit endet hier. Am Ende der nächsten Einheit wird es einen Hefteintrag geben, den ihr euch hier herunterladen und ins Heft kleben bzw. in eurem Ordner abheften könnt. | Diese Einheit endet hier. Am Ende der nächsten Einheit wird es einen Hefteintrag geben, den ihr euch hier herunterladen und ins Heft kleben bzw. in eurem Ordner abheften könnt. | ||
== Arbeitsauftrag Biologie6 (verpflichtend) == | |||
* Die folgende verpflichtende Unterrichtseinheit hat eine Bearbeitungszeit von ca. 45 Minuten. | |||
* Ihr benötigt für die Bearbeitung: Das Schulbuch, einen Zettel, Stift und Ruhe. | |||
* Bitte bearbeitet die gestellten Aufgaben tatsächlich erst selbst, bevor ihr auf die Lösung klickt! | |||
{{Box-spezial | |||
|Titel=<span style="color:#080">'''Wiederholung'''</span> | |||
|Inhalt= | |||
Ihr habt in der letzten Einheit Umweltfaktoren kennengelernt, die einen Einfluss auf Lebewesen haben können. | |||
* Zählt zur Wiederholung fünf solche Faktoren auf! | |||
{{Lösung versteckt| | |||
z.B. Temperatur, Wasserverfügbarkeit, Mineralstoffgehalt, Konkurrenz, Krankheitserreger, Parasiten | |||
|Lösung 1|Lösung ausblenden}} | |||
|Farbe= #080 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #DFB | |||
|Hintergrund= #DFB | |||
}} | |||
<br> | |||
{{Box-spezial | |||
|Titel=<span style="color:#080">'''Vitalitätskurven'''</span> | |||
|Inhalt= | |||
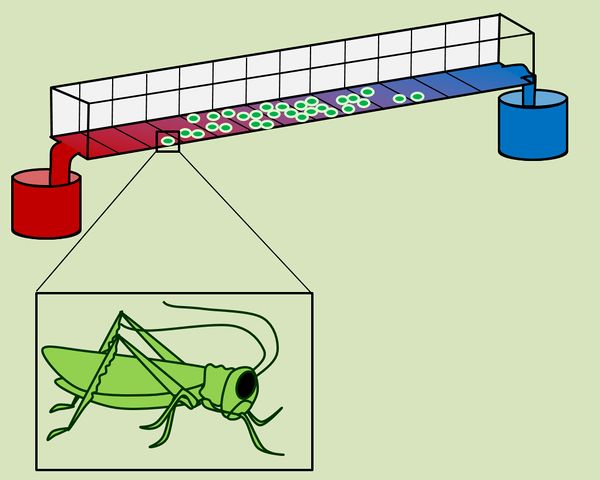
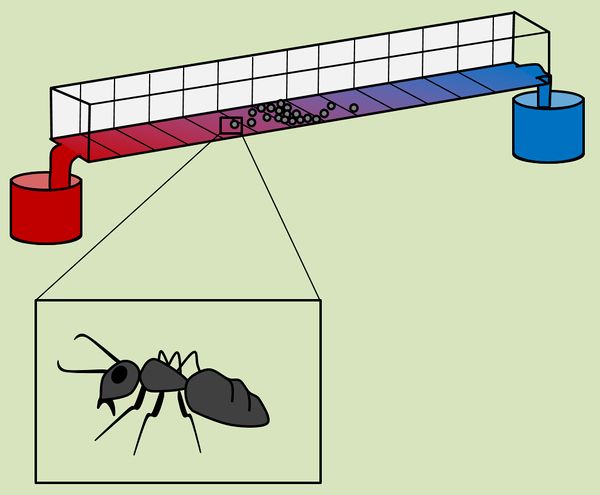
In dieser Einheit sollen die Auswirkungen von zwei abiotischen Faktoren auf Lebewesen etwas genauer unter die Lupe genommen werden. In einem relativ simplen Experiment wurde untersucht, wie die Individuen einer Gruppe auf den Faktor Temperatur reagieren: Eine Metall-Rinne wurde am einen Ende in heißes Wasser, am anderen Ende in Eiswasser getaucht. Da die Wärme vom heißen Wasser sich in Richtung des Eises ausbreitet, entstehen ein '''Temperatur-Gradient''' (auch '''Temperatur-Gefälle''' oder '''Temperatur-Orgel''' genannt). In diese Apparatur kann man kleine Lebewesen setzen, z. B. Heuschrecken und beobachten, wie sie sich verteilen. Das folgende Bild zeigt das Ergebnis: | |||
[[Datei:A6_TempOrgel_Heuschrecke.jpg|600px]]<br> | |||
<br> | |||
* Beschreibt das Ergebnis zunächst mit Worten! | |||
* Zeichnet dann eine Grafik, die auf der x-Achse die Temperaturabschnitte zeigen soll und auf der y-Achse die Anzahl der Tiere, die sich in den jeweiligen Temperaturabschnitten aufhalten! | |||
{{Lösung versteckt| | |||
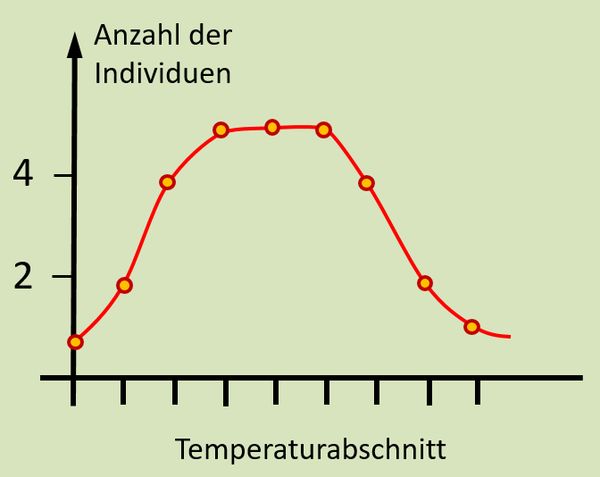
* z.B.: Die meisten Tiere bevorzugen eine mittlere Temperatur, nur wenige halten sich in ganz warmen oder ganz kalten Temperaturabschnitten auf | |||
<br> | |||
[[Datei:A6_TempOrgel_Heuschrecke_Grafik.jpg|600px]]<br> | |||
|Lösung 2|Lösung ausblenden}} | |||
|Farbe= #080 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #DFB | |||
|Hintergrund= #DFB | |||
}} | |||
<br> | |||
{{Box-spezial | |||
|Titel= | |||
|Inhalt= | |||
Die sich ergebende Kurve kann allgemein auf andere Umweltfaktoren übertragen werden und man könnte folgende Erklärung formulieren: Die meisten Lebewesen kommen mit einer mittleren Ausprägung eines Faktors (egal ob Temperatur, UV-Einstrahlung, Störgeräusche etc.) am besten klar. Je extremer die Ausprägung eines Merkmals (je heißer, je kälter, je lauter, je intensiver...) desto schwieriger fällt das Überleben.<br> | |||
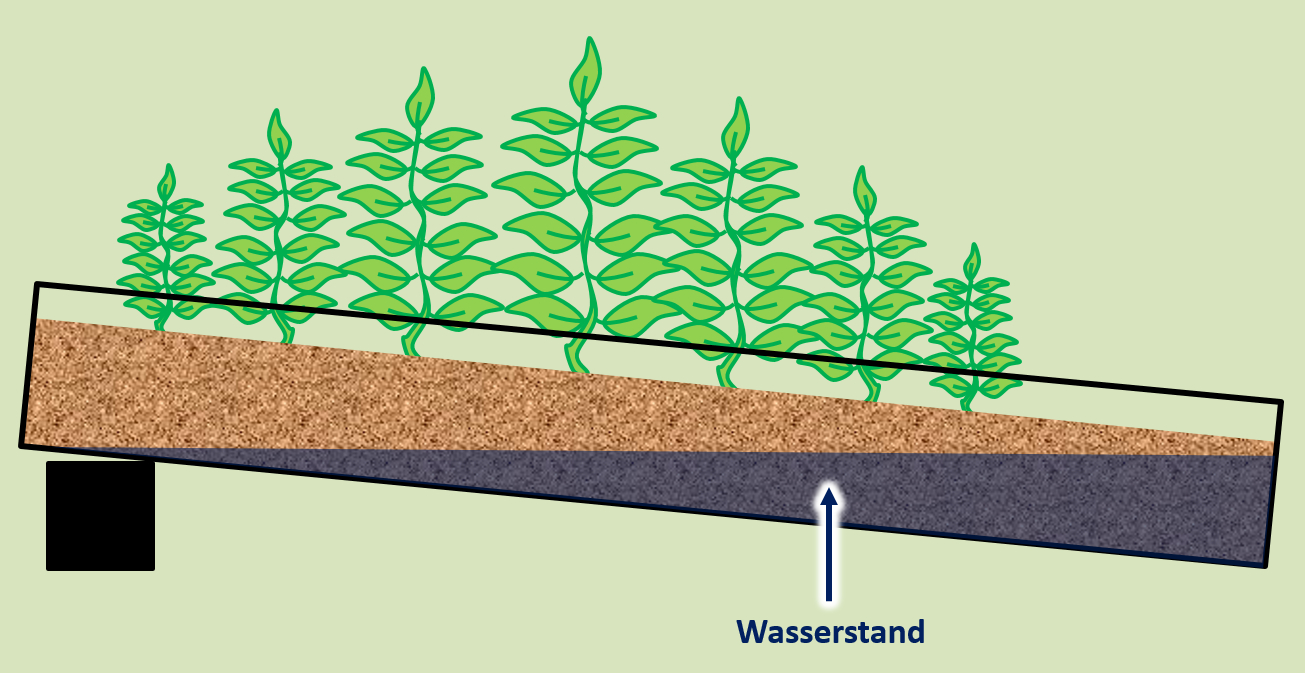
* Ein anderes Beispiel: Interpretiert die folgende Grafik bei der Pflanzen in einem "Wasserverfügbarkeits-Gradienten" gewachsen sind! | |||
[[Datei:A6_WasserverfügbarkeitsOrgel.jpg]]<br> | |||
<br> | |||
{{Lösung versteckt| | |||
* Die Grafik zeigt das Wachstum von Pflanzen in Abhängigkeit von der Wasserverfübgarkeit. Die Pflanzen wachsen am besten bei mittlerem Wasserstand, sie wachsen deutlich schlechter bei niedrigem oder hohem Wasserstand. | |||
|Lösung 3|Lösung ausblenden}} | |||
|Farbe= #080 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #DFB | |||
|Hintergrund= #DFB | |||
}} | |||
<br> | |||
{{Box-spezial | |||
|Titel= | |||
|Inhalt= | |||
Die beiden Kurven, die ihr jetzt kennengelernt habt sind typisch und gelten allgemein. Ihr könnt das z.B. in eurer Klasse überprüfen: Fragt, wie viele Stunden Schlaf jeder von euch braucht, um sich wohl zu fühlen. Fragt, wie lange ihr gerne im Sommer im Schwimmbad in der Sonne liegt. Fragt, welche Temperatur ihr in eurem Zimmer am angenehmsten empfindet.<br> | |||
Es sollte immer das gleich herauskommen: Die meisten werden einen mittleren Wert bevorzugen, ein paar wenige einen sehr hohen, ein paar wenige einen sehr niedrigen Wert. Man nennt die aus solchen Untersuchungen abgeleiteten Grafiken '''"Vitaltiätskurven"''': Auf der y-Achse wird immer eine '''"Vitalitätsmaß"''' angegeben. Das kann z.B. sein die '''Wachstumsrate''', die '''Aufenthaltsdauer''', der '''Ertrag''', die '''Aktivität'''... immer in Abhängigkeit von der Ausprägung des untersuchten Faktors (z.B. der Temperatur). Der Verlauf entspricht einer "Optimumskurve": Bei einem bestimmten Wert ist die Vitalität "optimal", sowohl "links" als auch "rechts" von diesem Wert fällt die Vitalität ab.<br> | |||
Bei allen Gemeinsamkeiten können sich die Kurven doch leicht unterscheiden. Im ersten hier beschriebenen Versuch mit der Temperatur-Orgel wurden Heuschrecken in die Rinne gesetzt, man kann aber auch Ameisen einer bestimmten Art verwenden. Das Ergebnis zeigt das folgende Bild.<br> | |||
[[Datei:A6_TempOrgel_Ameise.jpg|600px]]<br> | |||
<br> | |||
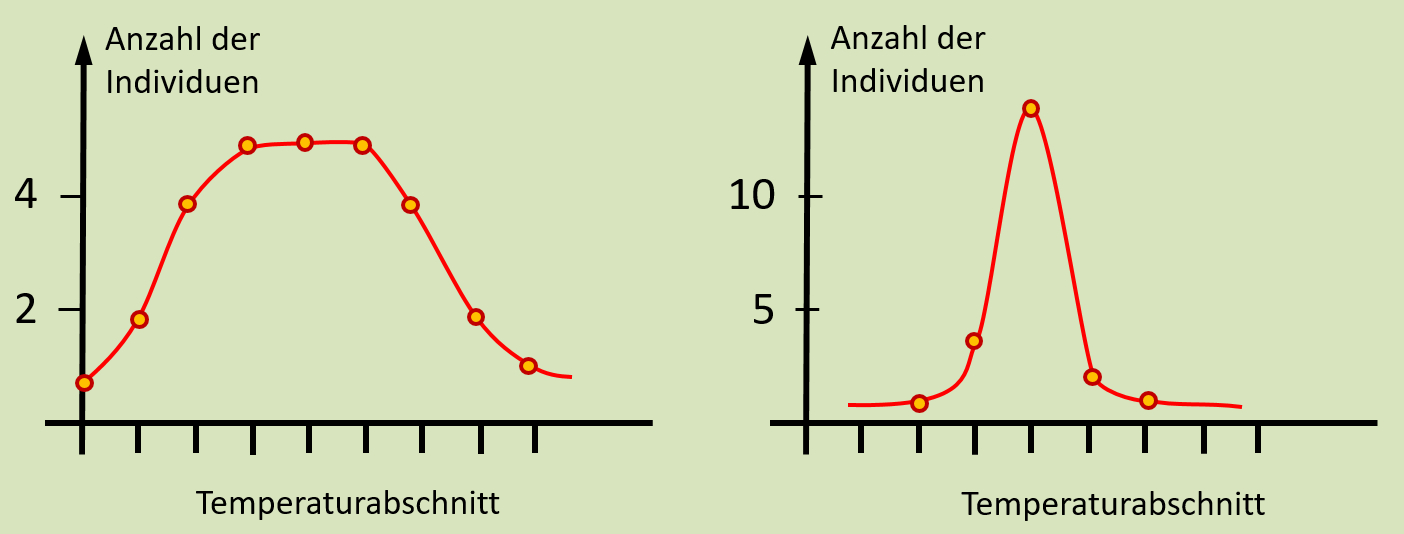
* Zeichnet genau wie beim ersten Versuch eine Grafik, welche die Anzahl der Individuen in den einzelnen Temperaturabschnitten zeigt. Zeichnet die Grafik genau rechts neben die erste (wenn kein Platz mehr auf dem Blatt ist, dann ein neues daneben legen). Versucht die Grafik so zu zeichnen, dass euer höchster y-Wert bei beiden Grafiken ungefähr auf gleicher Höhe liegt. | |||
* Beschreibt den Unterschied der beiden Grafiken! | |||
{{Lösung versteckt| | |||
[[Datei:A6_TempOrgel_Vergleich_Grafik.jpg]]<br> | |||
<br> | |||
* Bei der Grafik von den Ameisen halten sich nahezu alle im selben Temperaturbereich auf. Es gibt nur wenige Abweichler und die sind immer noch dicht bei den anderen. Lebewesen, die auf einen sehr engen Bereich bezüglich eines Umweltfaktors begrenzt sind, nennt man '''Spezialisten''', oder als Adjektiv: Sie sind '''stenök '''(wenn sie bezüglich vieler Faktoren Spezialisten sind) oder '''steno...''' wenn es nur um einen Faktor geht (hier also '''stenotherm''', weil sie Spezialisten bezüglich des Faktors Temperatur sind) | |||
* Bei der Grafik von den Heuschrecken erkennt man, dass sich die Heuschrecken über einen viel größeren Bereich verteilen. Tiere, die Umweltfaktoren in großen Schwankungen tolerieren nennt man '''Generalisten '''oder als Adjektiv: Sie sind '''euryök '''(wenn sie bezüglich vieler Faktoren Generalisten sind) oder '''eury...''' wenn es nur um einen Faktor geht (hier also '''eurytherm''', weil sie Generalisten bezüglich des Faktors Temperatur sind) | |||
|Lösung 4|Lösung ausblenden}} | |||
|Farbe= #080 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #DFB | |||
|Hintergrund= #DFB | |||
}} | |||
<br> | |||
{{Box-spezial | |||
|Titel=<span style="color:#080">'''Arbeitsauftrag'''</span> | |||
|Inhalt= | |||
* Lest jetzt im Buch die S. 70! | |||
* Verinnerlicht vor allen Dingen die Fachbegriffe, die zu bestimmten Teilen einer Vitalitätskurve gehören (Abbildung 2)! | |||
* Bearbeitet dann die Aufgabe 3a auf der Seite 71! | |||
{{Lösung versteckt| | |||
* Die Grafik zeigt die Wachstumsrate von Mehlwürmern in Abhängigkeit von der Temperatur und auch die Anzahl von Mehlwürmern, die sich in einem bestimmten Temperaturbereich aufhalten. Es ergibt sich eine typisch Optimumskurve: Bei ca. 32°C wachsen die Mehlwürmer am besten, hier liegt das Optimum. Sowohl bei niedrigeren also auch höheren Temperaturen geht die Wachstumsrate stark zurück. | |||
* Fachbegriffe für die Buchstaben: A-Toleranzbereich, B-Optimum, C-Pessimum, D(links)-Minimum, D(rechts)-Maximum | |||
|Lösung 5|Lösung ausblenden}} | |||
|Farbe= #080 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #DFB | |||
|Hintergrund= #DFB | |||
}} | |||
<br> | |||
{{Box-spezial | |||
|Titel=<span style="color:#080">'''Hausaufgabe'''</span> | |||
|Inhalt= | |||
Interpretiert auf der S. 70 die Abbildung 1 ausführlich (nur die durchgezogenen Linien, nicht die gestrichelten)! <br> | |||
Die Lösung wird im Laufe der Woche hochgeladen. | |||
|Farbe= #080 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #DFB | |||
|Hintergrund= #DFB | |||
}} | |||
<br> | |||
Der Hefteintrag für die letzten beiden Einheiten ist jetzt online verfügbar: | |||
Version vom 31. März 2020, 18:56 Uhr
Arbeitsauftrag Bio1
Arbeitsauftrag Bio2
Der Stängel ist vierkantig und hohl. [Hier ein Bild]
Arbeitsauftrag Bio3
Das erste Foto wird nach 24 Stunden hochgeladen (also am 25.03.)
Arbeitsauftrag Bio4
Dokumentation folgt am Mittwoch
Arbeitsauftrag Biologie5 (verpflichtend)
Damit ihr nicht ganze fünf Wochen ohne Biologie-Unterricht gewesen sein, bekommt ihr zum Auffrischen der Thematik in dieser Woche zwei kleine, verpflichtende Unterrichtseinheiten zur Verfügung gestellt.
- Die Einheit sollte ca. 30 Minuten dauern.
- Für die Bearbeitung benötigt ihr: Das Schulbuch, einen Zettel, einen Stift und Ruhe.
Diese Einheit endet hier. Am Ende der nächsten Einheit wird es einen Hefteintrag geben, den ihr euch hier herunterladen und ins Heft kleben bzw. in eurem Ordner abheften könnt.
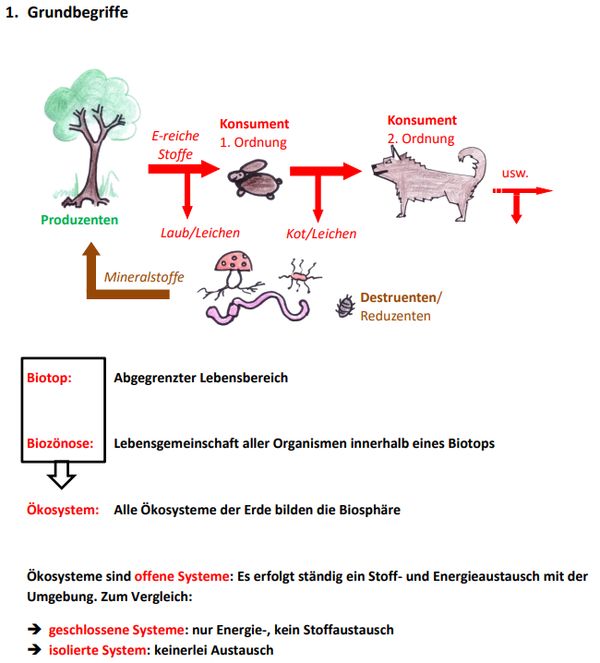
Arbeitsauftrag Biologie6 (verpflichtend)
- Die folgende verpflichtende Unterrichtseinheit hat eine Bearbeitungszeit von ca. 45 Minuten.
- Ihr benötigt für die Bearbeitung: Das Schulbuch, einen Zettel, Stift und Ruhe.
- Bitte bearbeitet die gestellten Aufgaben tatsächlich erst selbst, bevor ihr auf die Lösung klickt!
Der Hefteintrag für die letzten beiden Einheiten ist jetzt online verfügbar: