M6 4.2 Flächeninhalt eines Dreiecks

<6b 2020 21|Mathe 6b

Donnerstag, den 25.02.2021

Idee:

Wir haben gerade gesehen, dass man die Formel für den Flächeninhalt mit Hilfe des Parallelogramms herleiten kann. Es geht aber auch mit Hilfe des Rechtecks.

Höhe im Dreieck

Wie gerade gesehen, braucht man zur Berechnung des Flächeninhalts die Höhe. Im Dreieck gibt es 3 Stück davon. Wenn du dir unsicher bist, dann sieh dir folgendes Video an. Für alle, die an der Videokonferenz nicht teilnehmen konnten und das Video nicht ausreicht zur Erklärung. Hier gibt es noch drei Apps zum Verständnis.

EmbedVideo fehlt ein anzugebender Parameter.

Merkhefteintrag

4. 2 Flächeninhalt eines Dreiecks

Höhen im Dreieck:

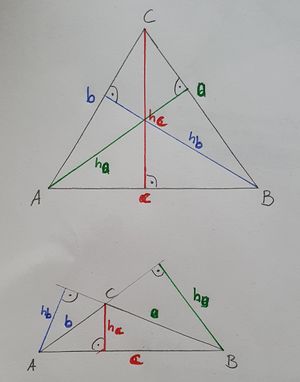
Unter den Höhen eines Dreiecks versteht man die Abstände der Eckpunkte von den gegenüberliegenden Seiten bzw. deren Verlängerungen (im Falle eines stumpfwinkligen Dreiecks).
Ein Dreieck hat drei Höhen.
Beispiel:
h_c ist der Abstand des Eckpunktes C von der Seite $\overline{AB}$ bzw. deren Verlängerung.

Zeichne auch die beiden Dreieck wie oben und alle drei Höhen, wie im vorhergehenden Erklärvideo gesehen.
Ist noch etwas unklar, dann schaue das Video nochmal! Oder springe ans Ende der Seite und bearbeite die letzte App .

Merke:

Vervollständige deinen Hefteintrag mit dem folgenden Merksatz!

Flächeninhalt eines Dreiecks

Der Flächeninhalt A eines Dreiecks ist gleich die Hälfte des Produkts aus der Seitenlänge und der zugehörigen Höhe.

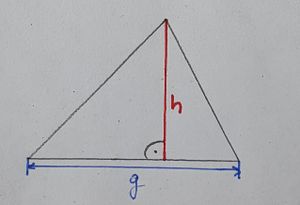
Allgemein gilt: $A = \frac {1}{2} \cdot g \cdot h = \frac {g\cdot h}{2} = (g\cdot h) \div2$, der Flächeninhalt ist die Hälfte des Produkts aus einer Seite (Grundseite g) und zugehöriger Höhe (h).

Anmerkung: Um klar zu machen, welche Höhe und welche Grunseite gemeint ist schreibt man auch oft:
$A = \frac {1}{2} \cdot a \cdot h_a$
$A = \frac {1}{2} \cdot b \cdot h_b$
$A = \frac {1}{2} \cdot c \cdot h_c$;

Berechnen von Flächeninhalten

Bearbeite S. 135/ 4
Wiederhole für dich nochmal die Lösungen zur Aufgabe 4, um zu sehen, ob du es verstanden hast. $A = \frac{1}{2} \cdot g \cdot h =...$

Lösung der Aufgaben:
S.135/4 a)
gegegben: g = 9 cm und h = 4 cm

$A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 9 cm \cdot 4 cm = \frac{1}{2} \cdot (9 cm \cdot 4 cm) = \frac {1}{2} 36 cm^2 = 18 cm^2$

b)
gegeben: g = 6 cm und h = 4 cm oder
gegeben: g = 4 cm und h = 6 cm
Zwei Seiten des Dreiecks stehen aufeinander senkrecht. Damit ist die eine Seite die Höhe zu der Seite, auf der sie senkrecht steht oder eben umgekehrt.

$A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 6 cm \cdot 4 cm = 3 cm \cdot 4 cm = 12 cm^2$

c)
gegeben: g = 3 cm und h = 3 cm

$A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 3 cm \cdot 3 cm = 4,5 cm^2$

d)
gegeben: g = 3,5 cm und h = 2,7 cm

$A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 3,5 cm \cdot 2,7 cm = 4,725 cm^2$

Zeichnen der Höhen und berechnen

Bearbeite S. 135/5
Bitte denkt daran, die Höhen auch einzuzeichnen und die Einheiten zu notieren.

Lösung der Aufgaben:

Flächeninhalt auf Karopapier

Bearbeite S. 135/9

Lösung der Aufgaben:
S.136/9
a) Links: $A= {1\over 2} \cdot g \cdot h ={ 1 \over 2} \cdot 5 \cdot 3 = 7,5$ [Kästchen]
Rechts: $A= {1\over 2} \cdot g \cdot h ={ 1 \over 2} \cdot 3 \cdot 5 = 7,5$[Kästchen]

oder in cm: Links: $A= {1\over 2} \cdot g \cdot h ={ 1 \over 2} \cdot 2,5cm \cdot 1,5 cm = 1,875 cm²$ [Kästchen]
Rechts: $A= {1\over 2} \cdot g \cdot h ={ 1 \over 2} \cdot 1,5 \cdot 2,5 = 1,875cm²$[Kästchen]
Die Dreiecke haben den gleichen Flächeninhalt.

b) Nicht die Höhe oder die Breite bestimmen den Flächeninhalt, sondern beide zusammen. (Kann auch von euch anders formuliert sein)

Dreiecke im Koordinatensystem

Du kannst hier die Höhen und Grundseiten leicht ablesen. (wie beim Paralellogramm Aufgabe 10)

Wiederholung der Brüche

Bearbeite S.126/11 c
Denke an eine fortlaufende Rechnung. Ich habe 7 Zeilen benötigt.

Lösung der Aufgaben:
S.126/11: Hier nur die Lösungen, wenn du Fehler hast und sie nicht findest, dann schicke mir deine Lösung.

c)$9 {11 \over 20}$

Abgabe

Lade bitte deinen Merkhefteintrag von heute und zum Parallelogramm im Modul Lernen hoch.

Zusätzliche Hilfen

Was sind die drei Höhen im Dreieck:

Lage der Höhen im Dreieck: Ziehe an einer Ecke des Dreiecks und schaue, wie die Höhen "wandern".

Messen der Höhe:

Nach oben

Freitag,den 26.02.2021

Guten Morgen!

Hast du die Einträge ins Merkheft zum Parallelogramm und Dreieck schon abgegeben?

Heute übst du weiter den Flächeninhalt vom Dreieck und das Zeichnen der Höhe.

Dreiecke im Koordinatensystem

Überlege dir erstmal, wie groß das Koordinatensystem werden muss. Diesmal sind auch negative Einträge dabei.
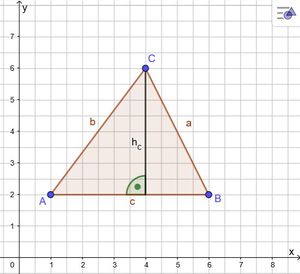
Prüfe nach jedem Aufgabenteil, ob du richtig gezeichnet und gerechnet hast. Bearbeite S. 136/8a, b, c.

Bitte prüfe auch deine Beschriftung der Achsen. Hast du auch an die Pfeile am Ende nach oben und rechts gedacht?
g = c = 6 - 1 = 5 [cm] und h_c = 6 - 2 = 4 [cm]

$A= {1 \over 2} \cdot 5cm \cdot 4cm = 10cm^2$

Bitte prüfe auch deine Beschriftung der Achsen. Hast du auch an die Pfeile am Ende nach oben und rechts gedacht?
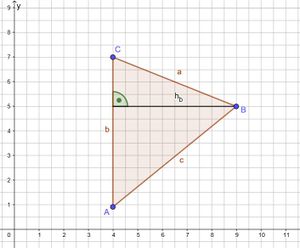
g = b = 7 - 1 = 6 [cm] und h_b = 9 - 4 = 5 [cm]

$A= {1 \over 2} \cdot 6cm \cdot 5cm = 15cm^2$

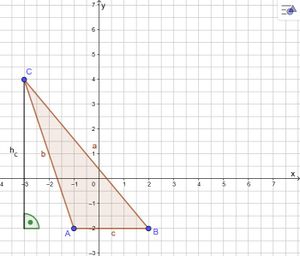
Oh, hier liegt die Höhe außerhalb des Dreiecks.
g = c = 2- (-1) = 3 [cm] und h_c = 4 -(- 2) = 6 [cm]

$A= {1 \over 2} \cdot 3cm \cdot 6cm = 9cm^2$

Berechnen der Höhe/Seite mit Hilfe des Flächeninhalts!

Es ist ein Parallelogramm gegeben mit:
A= 24cm² und g = 4cm

1. Schritt: Formel für den Flächeninhalt lautet: $A= g \cdot h$. Setze die gegebenen Werte ein. $24 cm^2 = 4cm \cdot h$
2. Schritt: Löse mit Hilfe der Umkehrrechnung: h = 24cm² : 4 cm = 6cm
   

Beim Berechnen der Grundseite mit Hilfe einer Höhe und des Flächeninhaltes geht es genauso.

Übung 1

Berechne die fehlende Größe beim Parallelogramm.

1. g = 5 cm; h = 7 cm; A=35() cm²
   
2. g = 12 cm; h =4() cm; A=48 cm²
   
3. g =4() cm; h = 8 cm; A= 32 cm²

Lösung der Aufgaben:
1) A= 5 cm* 7 cm = 35 cm²
2) h = 48 cm²:12 cm = 4 cm

3) g = 32 cm²:8 cm = 4 cm

Berechnen der Höhe/Seite mit Hilfe des Flächeninhalts!

Es ist ein ‚‘‘Dreieck‘‘‘ gegeben mit:
A= 18cm² und g = 4cm

1. Schritt: Formel für den Flächeninhalt lautet: $A= {1 \over 2} \cdot g \cdot h$. Setze die gegebenen Werte ein. $18 cm^2 = {1 \over 2} \cdot 4cm \cdot h$
   Hans rechnet:$18 cm^2 = 2 cm \cdot h$
   Britta rechnet: $36cm^2 = 4 cm \cdot h$ und denkt an das Parallelogramm, das man mit zwei Dreiecken erhält.
2. Schritt: Löse mit Hilfe der Umkehrrechnung:
   Hans: h = 18cm² : 2 cm = 9cm
   Britta: h = 36 cm² : 4 cm = 9cm
   

Beide haben somit recht mit ihrem Vorgehen.
Versuche die beiden Varianten zu verstehen. Wähle dann entweder Brittas oder Hans' Vorgehen, um in der folgenden Übung zu rechnen.

Beim Berechnen der Grundseite mit Hilfe einer Höhe und des Flächeninhaltes geht es genauso.

Übung 2

Berechne die fehlende Größe beim Dreieck. Prüfe dein Ergebnis, indem du mit deinem Wert nochmal den Flächeninhalt berechnest.

1. g = 4 cm; h = 8 cm; A=16() cm²
   
2. g = 4 cm; h =6() cm; A= 12 cm²
   
3. g =8() cm; h = 8 cm; A= 32 cm²

Lösung der Aufgaben:
1)$A= 1 \over 2 \cdot 4 cm \cdot 8 cm = 16 cm²$
2) h = 24 cm²:4 cm = 6 cm oder h = 12 cm² : 2 cm = 6 cm

3) g = 64 cm²:8 cm = 8 cm
oder g = 32cm²:8cm = 8cm

Übung 3

Bearbeite nun im Buch S.137/14a,b,d.

Textaufgabe

S.137/18

Tipp
1. Berechne die orangene Fläche.

2. Den Flächeninhalt mit den Kosten pro m² multiplizieren.

Freiwillige, da schwerere Aufgaben

• S.138/21 (rot)
• S.138/23 (wie S.142/16 und den Aufgaben S.137/14)

Lösungen

Die Lösung der letzten Aufgaben erhälst du am Mittwoch zum Kontrollieren.
Überprüfe nochmal, ob du alle Aufgaben für diese Woche erledigt hast.

Zum Wochenplan 14 habe ich schon einige Abgaben erhalten. Super!