M6 4.2 Flächeninhalt eines Dreiecks: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: „{{Box|1= Idee: |2= Wir haben gerade gesehen, dass man die Formel für den Flächeninhalt mit Hilfe des Parallelogramms herleiten kann. Es geht aber auch mit Hi…“) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 13: | Zeile 13: | ||
{{Box|Merkhefteintrag| | {{Box|Merkhefteintrag| | ||
'''4. 2 Flächeninhalt eines Dreiecks''' | '''4. 2 Flächeninhalt eines Dreiecks''' | ||
{{Box-spezial | |||
{{ | |Titel='''Höhen im Dreieck:''' | ||
'''Höhen im Dreieck:''' | |Inhalt= | ||
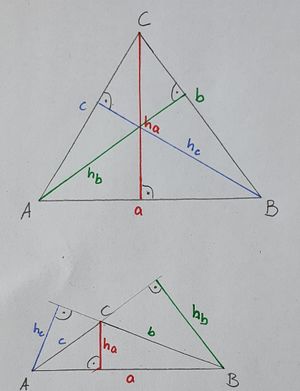
Unter den Höhen eines Dreiecks versteht man die Abstände der Eckpunkte von den gegenüberliegenden Seiten bzw. deren Verlängerungen (im Falle eines stumpfwinkligen Dreiecks). <br> Ein Dreieck hat drei Höhen. <br> | Unter den Höhen eines Dreiecks versteht man die Abstände der Eckpunkte von den gegenüberliegenden Seiten bzw. deren Verlängerungen (im Falle eines stumpfwinkligen Dreiecks). <br> Ein Dreieck hat drei Höhen. <br> | ||
''Beispiel:'' <br> | ''Beispiel:'' <br> | ||
h<sub>c</sub> ist der Abstand des Eckpunktes C von der Seite <math> \overline{AB} </math> bzw. deren Verlängerung. | h<sub>c</sub> ist der Abstand des Eckpunktes C von der Seite <math> \overline{AB} </math> bzw. deren Verlängerung. | ||
<br> | <br> | ||
[[Datei:Dreieck mit Höhen.jpg|mini]] | [[Datei:Dreieck mit Höhen.jpg|mini]] | ||
|Farbe= #828282 | |||
|Rahmen= 1 | |||
|Rahmenfarbe= #828282 | |||
|Icon = <i class="fa fa-angellist" aria-hidden="true"></i> | |||
}} | |||
Zeichne zwei Dreieck (wie im Buch) und alle drei Höhen, wie im vorgehenden Erklärvideo gesehen. <br> Ist noch etwas unklar, dann schaue das Video nochmal! | Zeichne zwei Dreieck (wie im Buch) und alle drei Höhen, wie im vorgehenden Erklärvideo gesehen. <br> Ist noch etwas unklar, dann schaue das Video nochmal! | ||
|3=Merksatz}} | |3=Merksatz}} | ||
Version vom 22. Februar 2021, 14:18 Uhr