6e Lernen zu Hause: Brüche und Dezimalbrüche

15.02.2021

Zur Wiederholung:

Kommaverschiebung bei der Division von Dezimalbrüchen... Ordne so zu, dass die Ergebnisse der Aufgaben jeweils gleich sind!

Zur Wiederholung:

Ordne die Brüche ihren Dezimalbrüchen passend zu! Hierbei kannst du auch gleich testen, ob du die Zusammenhänge zwischen periodischen Dezimalbrüchen und Brüchen schon ausreichend gelernt hast...

Zum Einstieg:

Bearbeite im Buch S. 125/ 7 b), f), i), j)!
Verbessere bitte deine Lösung mit der von mir - bitte nicht nur durchstreichen und das Ergebnis von mir daneben schreiben, du solltest schon verstehen, falls du einen Fehler gemacht hast, wo dieser ist und warum du ihn gemacht hast. Nur so kannst du es beim nächsten Mal besser machen.

Lösung der Aufgaben:

b)

$0,3 + \frac {2}{3} = \frac{3}{10} + \frac{2}{3} = \frac{9}{30} + \frac {20}{30} = \frac{29}{30}$
$\frac{2}{3}$ ist ein periodischer Bruch, daher sollte man diese Aufgabe mit Brüchen rechnen. Bei der Addition von Brüchen braucht man den Hauptnenner, hier ist dieser 30.

f)
$\frac {1}{5} \div 0,7 = \frac {1}{5} \div \frac{7}{10} = \frac{1}{5} \cdot \frac{10}{7} = \frac{1 \cdot 10}{5 \cdot 7} =\frac{1\cdot 2 \cdot 5}{5\cdot7} = \frac {2}{7}$
Rechne hier am Besten mit Brüchen - Erinnerung: man dividiert in dem man mit dem Kehrbruch multipliziert!
Eine Berechnung mit Dezimalbrüchen würde ich dir hier nicht empfehlen. Das Ergebnis wäre ein periodischer Dezimalbruch, wie du im Folgenden sehen kannst.

$\frac {1}{5} \div 0,7= 0,2 \div 0,7 = 2 \div 7 = 0,\overline{285714}$

Aber vielleicht hast du eine Stelle in vorheriger Aufgabe entdeckt, mit der man ganz schnell ans Ziel kommt? Es steht in der Lösung zuvor "2:7" und hier ist man, sofern man es sieht, ganz schnell, ohne auch nur einen einzigen Rechenschritt mit Brüchen zu bearbeiten, fertig: $2 \div 7 = \frac{2}{7}$, denn wie du weißt, steht der Bruchstrich für das "Geteilt-Zeichen"...

i)
$0,9 - \frac{3}{25} = 0,9 - \frac{12}{100} = 0,9 - 0,12 = 0,78$ oder aber auch $0,9 - \frac{3}{25} = \frac{9}{10} - \frac{3}{25} = \frac{45}{50} - \frac{6}{50} = \frac{39}{50}$

j)
$\frac{3}{8} \cdot 0,25 = \frac {3}{8} \cdot \frac {1}{4} = \frac{3\cdot 1}{8 \cdot4 } = \frac{3}{32}$ oder aber auch

$\frac{3}{8} \cdot 0,25 = \frac{375}{1000} \cdot 0,25 = 0,375 \cdot 0,25 = 0,09375$

Zur Übung:

Wie du sicher noch weißt, rechnet man Klammern zuerst, Potenz vor Punkt vor Strich und natürlich von links nach rechts... Dieses Wissen wirst du mit folgenden Aufgaben mit dem Rechnen mit Büchen und Dezimalbrüchen verknüpfen. Bearbeite nun im Buch S. 126/ 11 a) und 12 i!
Falls dein Ergebnis ein anderes sein sollte, dann vergleiche bitte deine Lösung Schritt für Schritt mit der von mir!
Falls dir mein Lösungsvorschlag in der Darstellung zu klein sein sollte, kannst du einfach auf die beiden Rechtecke unten rechts im Bild klicken und es vergrößert sich.

Zur Wiederholung:

Heute musstest du noch nicht wirklich Kürzen, eine Potenz kam auch noch nicht vor... ;-)
Um dieses Wissen zu wiederholen und weiter zu vertiefen, berechne bitte folgende Aufgaben:

a) $6 \cdot \frac{8}{9} =$
b) $\frac{12}{13} \cdot \frac{26}{15} =$
c) $\frac{15}{4} \div 5 =$
d) $\frac{48}{27} \div \frac{56}{45} =$
e) $\Bigl(2\frac{2}{3}\Bigr)^2=$
Verbessere bitte deine Lösung bitte mit der von mir.

Lösung der Aufgaben:

a)

$6 \cdot \frac{8}{9} = \frac{6\cdot 8}{9} = \frac{2\cdot 3 \cdot 8}{3 \cdot 3} = \frac {16}{3} = 5\frac {1}{3}$

b)
$\frac{12}{13} \cdot \frac{26}{15} = \frac {3\cdot 4 \cdot 2 \cdot 13 }{ 13 \cdot 3 \cdot 5} = \frac {8}{5} = 1\frac{3}{5}$

c)
$\frac{15}{4} \div 5 = \frac{15}{4\cdot 5} = \frac{3\cdot5}{ 4\cdot 5} = \frac{3}{4}$

d)
$\frac{48}{27} \div \frac{56}{45} = \frac{48}{27} \cdot \frac{45}{56} = \frac{2\cdot 3 \cdot 8 \cdot 5 \cdot 9}{3 \cdot 9 \cdot 7 \cdot 8} = \frac {10}{7} = 1\frac {3}{7}$

e)

$\Bigl(2\frac{2}{3}\Bigr)^2= \Bigl(\frac{8}{3}\Bigr)^2 = \frac{64}{9} = 7\frac{1}{9}$

Kopfrechnen:

Zur Wiederholung und zum Abschluss des Kapitels "Multiplizieren und Dividieren von Bruchzahlen":

Schlag bitte dein Mathebuch auf Seite 128/ 129 auf - hier findest du "Das Wichtigste auf einem Blick".
Gehe bitte Schritt für Schritt durch die einzelnen Abschnitte der beiden Seiten und hake für dich im Kopf ab, ob du "Vervielfachen und Teilen", "Multiplikation von Brüchen", "Division von Brüchen", "Doppelbruch", "Multiplikation von Dezimalbrüchen", "Division durch natürliche Zahlen", "Division durch Dezimalbrüche", "Endliche und periodische Dezimalbrüche" und "Umwandeln von periodischen Dezimalbrüchen in Brüche" jeweils verstanden hast.
Die Beispiele jeweils helfen sicherlich, dass du dich besser an die Einzelheiten des jeweiligen Themengebiets erinnern kannst.

Hinweis:

Falls du nun feststellst, dass du einzelne Punkte noch etwas mehr trainieren möchtest, kannst du auf Seite 129 f./ Bist du fit? Aufgaben dazu finden.... Bitte löse nicht alle auf einmal und für heute war es schon genug Mathematik, die Aufgabe laufen dir nicht davon!
Vielleicht ist ja auch schon alles klar und du brauchst überhaupt keine weitere Übung.
Die Lösung zu den Aufgaben findest du im Buch auf den Seiten 249/ 250.

17.02.2021

Info vorab:

Ein Dreieck hat drei Eckpunkte, welche man meistens mit A, B und C bezeichnet.
Weitere Bezeichnungen am Dreieck:
Winkel $\alpha$ liegt am Eckpunkt A, gegenüber vom Punkt A liegt die Seite a, Winkel $\beta$ liegt am Eckpunkt B, gegenüber von Punkt B liegt die Seite b und Winkel $\gamma$ liegt am Eckpunkt C, gegenüber vom Punkt C liegt die Seite c.
Mit folgendem Link kannst du dir die Beschreibung von eben bezüglich der Bezeichnungen am Dreieck noch einmal bildhaft verdeutlichen: Notationen am Dreieck

Zur Wiederholung:

Wie war das nochmal, wie hat man eigentlich einen Winkel gemessen und wie gezeichnet... Lege zuerst dein Geodreieck, einen Bleistift und dein Schulheft bereit, damit du während des Videos dein Geodreieck im Blick haben kannst und nach dem Video gleich selbst drei Winkel zeichnen kannst!
Bevor du mit dem Video startest, notiere dir bitte Wiederholung als Überschrift in dein Heft!
Sieh dir nun zunächst folgendes Video aufmerksam an!
Nun bist du an der Reihe, Zeichne einen Winkel $\alpha =$ 30°, einen Winkel $\beta =$ 45° und einen Winkel $\gamma =$ 140°!

Winkel messen und zeichnen:

EmbedVideo fehlt ein anzugebender Parameter.

Freiwillig:

Falls noch nicht alles klar ist, hilft dir das folgende Video noch etwas detaillierter beim Messen und Zeichnen von Winkeln... Wenn dir alles absolut klar ist, gehe bitte direkt zur nächsten Aufgabe!

FREIWILLIG:

EmbedVideo fehlt ein anzugebender Parameter.

Zur Wiederholung:

Das Haus der Vierecke - vielleicht erinnerst du dich ja noch daran...
Bevor du dir das folgende Video anschaust, überlege zunächst einmal, welche verschiedene Arten von Vierecken es gibt, was sind jeweils ihre Besonderheiten!
Wenn du magst, kannst du zur jeder Viereckart eine kleine Skizze anfertigen und die wichtigen Eigenschaften farbig hervorheben.
Sieh dir nun noch folgendes Video aufmerksam an! Und passe ganz besonders gut beim Abschnitt zum Parallelogramm auf, das brauchen wir morgen. Konntest du dich an alle Viereckarten erinnern?

Viereckarten und ihre Besonderheiten:

EmbedVideo fehlt ein anzugebender Parameter.

Zur Vorbereitung:

Nun hast du es bald für heute geschafft... Nur noch ein paar letzte Fragen: Wie berechnet man eigentlich den Flächeninhalt von einem Rechteck? Wie berechnet man seinen Umfang? Was ist der Unterschied zwischen Flächeninhalt und Umfang? Du erinnerst dich sicher noch. Falls nicht, dann kannst du dies gerne - entweder in deiner Grundwissenmappe oder hier - unter 5. Umfang und Flächeninhalt - nachlesen: Grundwissen 5. Klasse.
Hab einen schönen Tag! Viele Grüße!

18.02.2021

Zur Wiederholung:

Bevor es los geht, notiere zuerst Flächeninhalt eines Parallelogramms als Überschrift in dein Schulheft!
Erinnere dich an die Formel zur Berechnung des Umfangs eines Rechtecks! Berechne nun den Umfang eines Rechtecks mit den Seiten a = 3 cm und b = 5 cm!

Anmerkung:

Um den Umfang eines Rechtecks zu berechnen, addiert man alle Seitenlängen des Rechtecks, d.h. $U = a + b + c + d = a + b + a + b = 2 \cdot a + 2 \cdot b$, da a = c und b = d!
Nun zur Lösung der Aufgabe:

$U = 2 \cdot a + 2 \cdot b= 2 \cdot 3 cm + 2 \cdot 5 cm = 6 cm + 10 cm = 16 cm$

Überlegung:

Schau dir nebenstehende Skizze genau an und überlege dir, wie man allgemein den Umfang eines Parallelogramms bestimmen könnte!
Notiere dir die "versteckte Lösung" als Merksatz in dein Schulheft, übertrage auch die Skizze des Parallelogramms in dein Heft!

Merke:

Der Umfang eines Parallelogramms ist die Summe aller Seitenlängen. Für den Umfang eines Parallelogramms ABCD mit den Seitenlängen a, b, c, d gilt:

$U = a + b + c + d = 2 \cdot a + 2 \cdot b$; a = c und b = d

Zur Wiederholung:

Erinnere dich an die Formel zur Berechnung des Flächeninhalts eines Rechtecks! Berechne nun den Flächeninhalt eines Rechtecks mit den Seiten a = 3 cm und b = 5 cm!

Anmerkung:

Der Flächeninhalt eines Rechtecks wird berechnet, indem man "Länge mal Breite" rechnet, d.h. $A= l \cdot b$ oder aber auch $A= a \cdot b$, je nachdem, welche Bezeichnung für die Seitenlängen des Rechtecks gewählt wurde...

Nun zur Lösung der Aufgabe:

$A = a \cdot b= 3 cm \cdot 5 cm = 15 cm ^2$

Überlegung:

Versuche nun herauszufinden, wie der Flächeninhalt eines Parallelogramms bestimmt werden kann. Dazu benötigst du ein Blatt Papier - gerne bunt - eine Schere, einen Stift, ein Geodreieck und eine gute Idee...

Zeichne ein Parallelogramm ABCD mit der Länge a = 9 cm und d = 5 cm sowie α = 60°.
Versuche nun den Flächeninhalt des Parallelogramms zu bestimmen!
Am Montag in der 2. Stunde werden wir die Lösung zur Berechnung des Flächeninhalts eines Parallelogramms gemeinsam in einer Videokonferenz besprechen. Den Link dazu erhältst du rechtzeitig im Schulmanager - Modul Lernen.

Zur Wiederholung:

Hier wirst du heute nun noch etwas zu Flächeninhalt und Umfang von Rechtecken üben!
Beachte bitte, dass du das Ergebnis jeweils mit der richtigen Einheit angibst und zwischen der Zahl und der Einheit ein Leerzeichen tippst, sonst wird die Lösung als falsch angezeigt, auch wenn du richtig gerechnet hast... Wichtig ist auch für z.B. m² "m Alt Gr 2" zu tippen, sonst würde eine richtige Lösung auch als falsch angezeigt werden...

Zur Wiederholung:

Zum Abschluss heute noch etwas Umrechnen von Einheiten - zunächst Längeneinheiten... Du musst hier nicht alle Aufgaben bearbeiten, sollten dir die einfachen zu einfach sein, dann lass sie bitte einfach weg, die zu "schwieriger" sind jedoch Pflicht!
Zum Reinkommen in das Umrechnen von Einheiten können die "einfachen" Aufgaben aber auch hilfreich sein, dies entscheidest du aber vollkommen selbstständig, je nachdem, wie gut du dich noch an das Umrechnen von Einheiten erinnern kannst!

Zur Wiederholung:

Und nun noch etwas Umrechnen von Einheiten - ein paar Flächeneinheiten...

Hab ein schönes Wochenende! Bis Montag zur Videokonferenz, ich bin schon gespannt auf deine Idee zur Berechnung des Flächeninhalts von Parallelogrammen.

22.02.2021

WICHTIG:

Bitte noch nicht weiter auf dieser Seite lesen, wir treffen uns erst in der Videokonferenz, um uns über eure Ideen zur Bestimmung des Flächeninhalts eines Parallelogramms auszutauschen... Hier geht es für dich erst nach der Konferenz weiter!
Falls du dann nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite, dann sollte es normalerweise klappen...

Idee:

Herleitung der Formel zur Berechnung des Flächeninhalts A eines Parallelogramms:
Hier kannst du dir nun nochmal Schritt für Schritt anschauen, wie der Flächeninhalt eines Parallelogramms bestimmt werden kann.

Wichtig:

Zur Berechnung des Flächeninhalts eines Parallelogramms benötigt man die Höhen im Parallelogramm. Mit folgender Darstellung kannst du erkennen, wie die Höhe im Parallelogramm dargestellt wird. Verschiebe die Höhen oder auch die Punkte des Parallelogramms mit deiner Maus und beschreibe , was dir dabei auffällt!
Notiere dir im Anschluss die beiden folgenden Merksätze in dein Heft!

Merke:

Höhen im Parallelogramm
Unter den Höhen eines Parallelogramms versteht man die Abstände der zueinander parallelen Seiten des Parallelogramms. Ein Parallelogramm hat zwei Höhen.
Man zeichnet die Höhe, indem man eine Strecke rechtwinklig zu einer Seite zeichnest und diese mit der dazu parallelen Seite verbindest.

Merke:

Flächeninhalt eines Parallelogramms
Der Flächeninhalt A eines Parallelogramms ist gleich dem Produkt aus der Seitenlänge und der zugehörigen Höhe.

A = a∙h_a oder A = b∙h_b; allgemein gilt: A = g∙h, der Flächeninhalt ist das Produkt aus einer Seite (Grundseite g) und zugehöriger Höhe (h).

Übung:

Bevor du mit den Übungen startest, solltest du alles gut verstanden haben! Falls noch irgendetwas unklar sein sollte, schau dir bitte am Ende der Seite das entsprechende Erklärvideo an. Vermutlich ist dir klar, wie man den Umfang und auch den Flächeninhalt eines Parallelogramms berechnet, aber kannst du auch eine Höhe ins Parallelogramm einzeichnen?
Falls du nicht mehr so genau weißt, wie man hierbei das Geodreieck anlegen sollte, findest du am Ende der Seite auch hierzu ein Erklärvideo.
Falls nun alles klar ist, starte bitte mit den Aufgaben! Zuerst B. S. 140/ 5 b) und c) - überlege dir jeweils genau, was ist die Seite des Parallelogramms, was die zugehörige Höhe. Vergleiche im Anschluss bitte deine Lösung mit meinem Lösungsvorschlag.
Erinnerung: Notiere dir stets, was gegeben ist und schreibe auch immer die Formel auf, die du zur Bearbeitung der Aufgabe verwendest.

Lösung der Aufgaben:

b)

g = 3,8 cm und h = 2,2 cm
$A = g \cdot h = 3,8 cm \cdot 2,2 cm = 8,36 cm^2$

c)
g = 5,6 cm und h = 3 cm

$A = g \cdot h = 5,6 cm \cdot 3 cm = 16,8 cm^2$

Übung:

Bearbeite B. S. 140/ 2! Vergleiche im Anschluss bitte deine Lösung mit meinem Lösungsvorschlag.

Lösung der Aufgabe:

a)

Alle Parallelogramme sehen zwar unterschiedlich aus, aber alle Parallelogramme haben denselben Flächeninhalt. Denn immer ist g = 1,5 cm und h = 1,8 cm
$A = g \cdot h = 1,5 cm \cdot 1,8 cm = 2,7 cm^2$

b)

Parallelogramme mit gleich langen (Grund-)seiten und gleich langer zugehöriger Höhe haben denselben Flächeninhalt, da das Produkt $A = g \cdot h$ immer dasselbe Ergebnis ergibt.

Übung:

Nun darfst du selbst die Höhe suchen.... und hoffentlich finden! Falls das noch nicht so gut klappen sollte, nochmal der Hinweis auf das Video am Ende der Seite zum Zeichnen der Höhen beim Parallelogramm.

Zur Vertiefung:

Bearbeite B. S. 141/ 7! Vergleiche im Anschluss bitte deine Lösung mit meinem Lösungsvorschlag.
Zusatz: Berechne den Umfang des skizzierten Parallelogramms!

Lösung der Aufgabe:

• Richtig ist: $A = 3 m \cdot 15 cm = (3 m \cdot 0,15 m) = 300 cm \cdot 15 cm = 4500 cm ^2 = 45 dm^2 = 0,45 m^2$

• Sophie hat den richtigen Ansatz. Sie hat jedoch vergessen 3 m in 300 cm umzurechnen, beziehungsweise 15 cm in 0,15 m. Zum Multiplizieren benötigen beide Größen die gleiche Einheit!
  
• Felix hat einen völlig falschen Ansatz. Er berechnet mit seinem Ansatz den halben Umfang, was jedoch nicht der Aufgabenstellung entspricht!
  
• Laura hat an das Umrechnen gedacht, jedoch hat sie die Seitenlänge anstatt der zugehörigen Höhe verwendet. Die auf der Grundseite stehende Höhe ist 15 cm lang! $A = g \cdot h$!
  Es ist falsch zur Berechnung dieses Parallelogramms die beiden Seitenlängen zu multiplizieren.
  

Lösung Zusatz:

$U = a + b + c + d = 2 \cdot a + 2 \cdot b = 2 \cdot 3 m + 2 \cdot 17 cm = 6 m + 34 cm = 600 cm + 34 cm = 634 cm = 6,34 m$

Freiwillig:

Falls noch etwas unklar geblieben sein sollte, kannst du dir folgende Videos anschauen!
Zum einen wird hier noch einmal die Berechnung des Umfangs und des Flächeninhalts eines Parallelogramms erklärt, zum anderen aber auch noch einmal, wie man mit Hilfe eines Geodreiecks eine Höhe in ein Parallelogramm einzeichnet und was man dabei beachten muss. Dieses Wissen ist, wie du weißt, sehr wichtig, um den Flächeninhalt eines Parallelogramms berechnen zu können!

Umfang eines Parallelogramms:

EmbedVideo fehlt ein anzugebender Parameter.

Flächeninhalt eines Parallelogramms:

EmbedVideo fehlt ein anzugebender Parameter.

Einzeichnen der Höhen - 1:

EmbedVideo fehlt ein anzugebender Parameter.

Einzeichnen der Höhen - 2:

EmbedVideo fehlt ein anzugebender Parameter.

24.02.2021

Übung:

Bevor du startest weiderhole bitte für dich die Formel zur Berechnung des Flächeninhalts eines Parallelogramms und auch die Formel zur Berechnung seines Umfangs. Solltest du feststellen, dass noch etwas unklar ist, dann schau dir bitte entsprechend das Erklärvideo der vergangenen Stunde an. Danke!
Wenn alles klar ist, dann geht's auch schon los....

Bearbeite bitte im Buch S. 141/ 6!
Berechne Zeile für Zeile und verbessere immer direkt im Anschluss deine Lösung mit dem folgenden Lösungsvorschlag.
Lass dich nicht irritieren, du fertigst im Heft nur eine Skizze des Parallelogramms - hier ist mehr als eine Skizze, dies dient der besseren Übersichtlichkeit und Nachvollziehbarkeit der Lösung.

Wenn du richtig gezeichnet hast, dann müsste die Seite $\overline{AB} = a$ ca. 3cm sein und die zugehörige Höhe ca. 1,7cm.
Der Flächeninhalt ist dann: A=3cm•1,7cm=5,1cm²

Sollten deine Werte um 1-2mm abweichen ist das kein Problem.

Die Länge der Seite $\overline{BC} = b$ ist ca. 2,1cm die zugehörige Höhe ist ca. 2,5cm.
Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². Sollten deine Werte um 1-2mm abweichen ist das kein Problem.

Die Länge der Seite $\overline{CD} = c$ ist ca. 3cm, c =a! Die zugehörige Höhe ist dann ebenfalls, wie auch die Höhe zur Seite a, ca. 1,7cm.
Mit diesen Werten kommt man auf einen Flächeninhalt von 5,1cm².

Die Länge der Seite $\overline{DA} = d$ ist ca. 2,1cm, d = b! Die zugehörige Höhe ist, wie auch die Höhe zur Seite b, ca. 2,5cm. Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm².

Feststellung und Begründung:

Unterschiede im Flächeninhalt entstehen aufgrund von Messungenauigkeiten. Eigentlich sollte bei jeder Messung und Rechnung immer der gleiche Flächeninhalt herauskommen, die Fläche des Parallelogramms verändert sich ja nicht....

Übung:

Bearbeite B. S. 142/ 12 a), b), c)!
Vergiss nicht die Anwendungsmöglichkeit einer Umkehrrechnung...

Lösung der Aufgaben:

a)

g = 16,2 cm und h = 3,5 cm
$A = g \cdot h = 16,2 cm \cdot 3,5 cm = 56,7 cm^2$
NR: $162\cdot 35 = 5670$, da die beiden Faktoren zusammen zwei Nachkommastellen haben, ist das Ergebnis für den Flächeninhalt 56,7(0) cm². Vergiss bitte nicht "$cm \cdot cm = cm^2$"!

b)
h = 5,2 cm und A = 22,36 cm²
Löse mit der Umkehraufgabe:
$g= A \div h = 22,36 cm^2 \div 5,2 cm = 223,6 cm^2 \div 52 cm = 4,3 cm$
Vergiss bitte nicht "$cm^2 \div cm = cm$"! Das Ergebnis muss eine Länge sein!

c)
Am besten du rechnest beide Größen sofort in dieselbe Einheit um!
g = 150 cm und A = 9,75 m² = 975 dm² = 97500 cm²
Löse mit der Umkehraufgabe:

$h= A \div g = 97500 cm^2 \div 150 cm = 650 cm = 6,5 m$
Vergiss auch hier bitte nicht "$cm^2 \div cm = cm$"! Das Ergebnis muss eine Länge sein!

Übung:

Bearbeite B. S. 142/ 16!
Vergiss auch hier nicht die Anwendungsmöglichkeit einer Umkehrrechnung...

Lösung der Aufgabe:

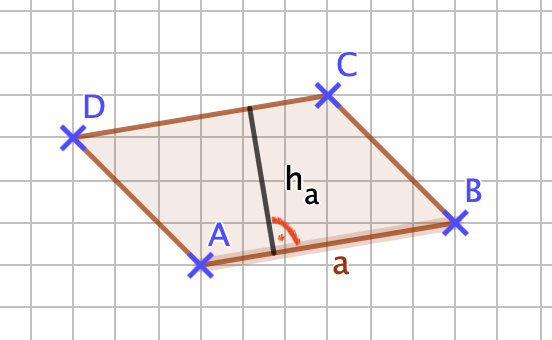
Berechne zuerst den Flächeninhalt A! A = a•h_a =5,7cm •2,5cm = 14,25cm²
NR: $57\cdot 25 = 1425$, da die beiden Faktoren zusammen zwei Nachkommastellen haben, ist das Ergebnis für den Flächeninhalt 14,25 cm². Vergiss bitte nicht "$cm \cdot cm = cm^2$"!

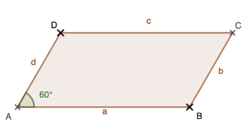
Nun weiß man, dass A = 14,25 cm². Man kennt auch die Seitenlänge der anderen Seite des Parallelogramms: b = 3,5 cm.

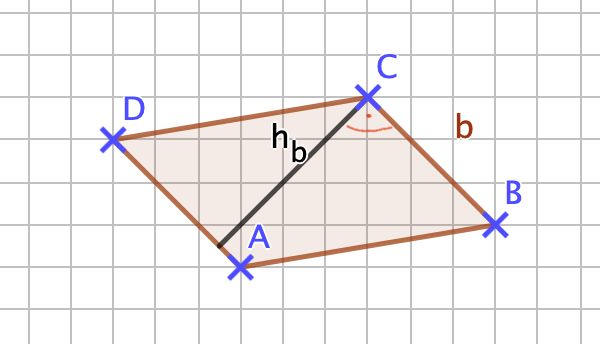
Den Flächeninhalt des Parallelogramms könnte man auch bestimmen, indem man A = b•h_b berechnet.
Damit kann man nun die zur Seite b gehörige Höhe mit Hilfe einer Umkehrrechnung wie folgt berechnen:
h_b = A : b = 14,25 cm² : 3,5 cm = 142,5 cm² : 35 cm ≈ 4,1 cm.
Anmerkung: Das richtige Endergebnis bei dieser Aufgabe zu berechnen ist ehrlich gesagt gar nicht so wichtig, hier zählt es mehr den Rechenweg verstanden zu haben.
Hier noch einmal kurz zusammengefasst: Man berechnet zunächst mit der Seitenlänge a = 5,7 cm und der zugehörigen Höhe h_a=2,5 cm den Flächeninhalt A des Parallelogramms und mit der Kenntnis dieses Flächeninhalts kann man nun h_b mit Hilfe einer Umkehraufgabe berechnen, indem man "A : b" berechnet und als Ergebnis die Höhe h_a erhält.

Test und Hausaufgabe:

B.S.142/ 18
Tipp: Eine Skizze kann für einen ersten Überblick hilfreich sein, zeichne gegebene Längen mit Farbe ein.
WICHTIG: Lade bitte die Lösung deiner Hausaufgabe im Schulmanager - Modul Lernen hoch! Danke! Ich würde gerne einmal einen Blick darauf werfen...