M5 V Flächeninhalt: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 26: | Zeile 26: | ||
|Üben}} | |Üben}} | ||
== Flächeninhalt und Umfang von Rechtecken== | ==Flächeninhalt und Umfang von Rechtecken== | ||
{{Box|Kästchen zählen| | {{Box|Kästchen zählen| | ||
Ihr kennt bereits die verschiedenen geometrischen Figuren. | Ihr kennt bereits die verschiedenen geometrischen Figuren. | ||
| Zeile 33: | Zeile 33: | ||
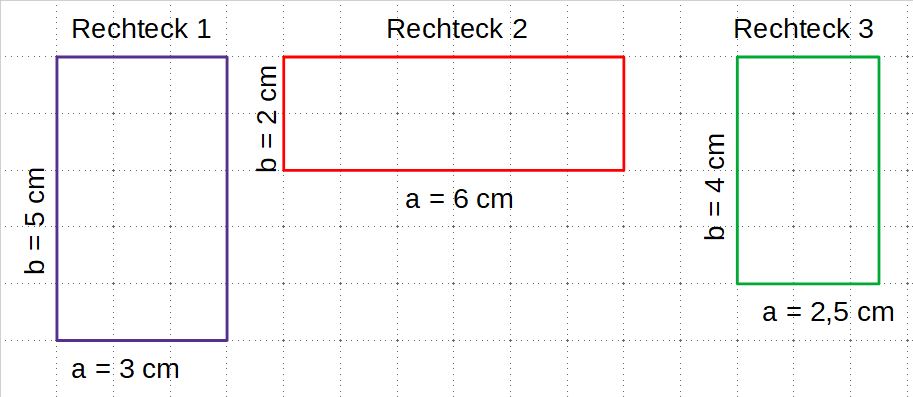
Betrachtet dazu die Zeichnungen und ermittelt, aus wie vielen Kästchen die Rechtecke bestehen. | Betrachtet dazu die Zeichnungen und ermittelt, aus wie vielen Kästchen die Rechtecke bestehen. | ||
[[Datei:Rechtecke01.jpg|midi]] | |||
{{Lösung versteckt| Rechteck 1 = 15 Kästchen; Rechteckt 2 = 12 Kästchen; Rechteck 3 = 10 Kästchen}} | |||
|Üben}} | |Üben}} | ||
{{Box|Info| | {{Box|Info| | ||
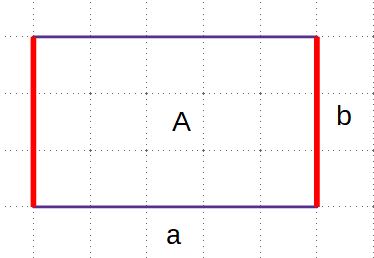
Bei einem Rechteck bezeichnet man die Seiten mit a und b. | |||
Bei einem Rechteck bezeichnet man die Seiten mit a und b. | [[Datei:Rechteck02.jpg|midi]] | ||
|Unterrichtsidee}} | |Unterrichtsidee}} | ||
{{Box|1 = | {{Box|1 = Zeichnen von 3 Rechtecken|2= | ||
* Zeichne ein Rechteck mit den Maßen a = 3cm; b = 4cm, ein Rechteck mit den Maßen a= 2cm und b = 6cm und das dritte Rechteck hat die Seitenlängen a = 8cm und b = 1,5 cm. Notiere die Seitenlängen am Rechteck. | * Zeichne ein Rechteck mit den Maßen a = 3cm; b = 4cm, ein Rechteck mit den Maßen a= 2cm und b = 6cm und das dritte Rechteck hat die Seitenlängen a = 8cm und b = 1,5 cm. Notiere die Seitenlängen am Rechteck. | ||
* Aus wie vielen 1cm² bestehen die Rechtecke? (Zur Erinnerung: 1cm² hat die Maße 1cm x 1cm, also 4 Kästchen) (Bild) | * Aus wie vielen 1cm² bestehen die Rechtecke? (Zur Erinnerung: 1cm² hat die Maße 1cm x 1cm, also 4 Kästchen) (Bild) | ||
| Zeile 54: | Zeile 53: | ||
|3 = Üben}} | |3 = Üben}} | ||
{{Box|1=Info|2= | |||
Möchte man den Flächeninhalt eines Rechtecks bestimmen, so kann man es erst einmal in gleich große Streifen zerlegen. | Möchte man den Flächeninhalt eines Rechtecks bestimmen, so kann man es erst einmal in gleich große Streifen zerlegen. | ||
Der Flächeninhalt A dieses Rechtecks beträgt also: <math>A = 3 cm \cdot 4 cm = 12 cm^2</math> | |||
|3=Unterrichtsidee}} | |||
{{Box|Merke| | {{Box|1=Merke|2= | ||
'''Flächeninhalt des Rechtecks'''<br> | |||
Der Flächeninhalt A eines Rechtecks mit den Seitenlängen a und b: | Der Flächeninhalt A eines Rechtecks mit den Seitenlängen a und b: | ||
# Der Flächeninhalt eines Rechtecks ergibt sich aus dem Produkt der Seitenlängen. | |||
# Der Flächeninhalt eines Rechtecks ergibt sich aus dem Produkt der Seitenlängen. | # Es gilt also: <math>A = a \cdot b</math> | ||
# Es gilt also: | |3=Merksatz}} | ||
|Merksatz}} | |||
{{Box|Notiere in dein Heft:| | {{Box|Notiere in dein Heft:| | ||
<u>Formeln für den Flächeninhalt und den Umfang von Rechtecken.</u><br> | |||
* Ergänze aus dem Buch S.230 den Merkkasten.<br> | |||
* Schreibe auch den Merkkasten zum Umfang S.231 darunter. | |||
Ergänze aus dem Buch S.230 den Merkkasten. | |Arbeitsmethode}} | ||
Schreibe auch den Merkkasten zum Umfang S.231 darunter. | |||
Arbeitsmethode}} | |||
{{Box|1=Übung 1|2= | |||
# Berechne nun auch den Flächeninhalt der anderen beiden Rechtecke Seitenlängen a = 8 cm und b = 1,5 cm sowie das Rechteck a = 2 cm und b = 6 cm, die du in dein Heft gezeichnet hast. | |||
''Tipp:''Wandle bei Kommazahlen beide Seitenlängen in die nächstkleinere Einheit um und rechne dann. | |||
# Berechne nun auch unter/neben den Rechtecken den Umfang. Was fällt dir auf? | # Berechne nun auch unter/neben den Rechtecken den Umfang. Was fällt dir auf? | ||
{{Lösung versteck|Lösung: Der Flächeninhalt bei allen drei Rechtecken ist gleich. Aber der Umfang ist unterschiedlich.}} | |||
|3=Üben}} | |||
{{Box|1=Übung 2|2= | |||
Berechne den Flächeninhalt A und den Umfang U der folgenden Rechtecke mit den Seitenlänge. Achte auch auf die Einheiten. | Berechne den Flächeninhalt A und den Umfang U der folgenden Rechtecke mit den Seitenlänge. Achte auch auf die Einheiten. | ||
| Zeile 106: | Zeile 96: | ||
d) a = 23 m, b = 8 m | d) a = 23 m, b = 8 m | ||
{{Box| Übung 3| | |3=Üben}} | ||
{{Box|Achtung| | |||
Man kann nur Seitenlängen mit gleicher Einheit miteinander multiplizieren! | |||
|Hervorhebung1}} | |||
{{Box| 1=Übung 3|2= | |||
Berechne jeweils den Flächeninhalt der Rechtecke in einer geeigneten Einheit. | Berechne jeweils den Flächeninhalt der Rechtecke in einer geeigneten Einheit. | ||
| Zeile 122: | Zeile 120: | ||
f) b = 5 m, c= 200 cm (Gib hier den Flächeninhalt in dm² an.) | f) b = 5 m, c= 200 cm (Gib hier den Flächeninhalt in dm² an.) | ||
|Üben}} | |||
|3=Üben}} | |||
Version vom 9. Juli 2020, 10:00 Uhr
1 Flächenvergleich
2 Einheiten für Flächeninhalte
Flächeninhalt und Umfang von Rechtecken