Mathematik 12/Integralrechnung: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 10: | Zeile 10: | ||
}} | }} | ||
{{Box-spezial | |||
|Titel= Unter- und Obersumme | |||
|Inhalt= [[bild:Int_abb1.png|220px|right]] | |||
:'''Aufgabe 1''': Gegeben ist die Funktion f(x) = 0.25 x². | |||
::#Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft. | |||
::#Berechne die zugehörige Ober- und Untersumme. | |||
::#Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an. | |||
::#Lösung: | |||
<popup name="Lösung"> | |||
Wir zerlegen das [0;4] in 8 Teilintervalle. Jedes Teilintervall ist 0,5 breit. <br>Zu den x-Werten 0; 0,5; 1; 1,5;.....4 gehören die folgenden y-Werte: | |||
x | 0 0,5 1 1,5 2 2,5 3 3,5 4 | |||
----------------------------------------------------------- | |||
f(x)| 0 0,0625 0,25 0,5625 1 1,5625 2,25 3,0625 4 | |||
Für den '''Flächeninhalt der Obersumme''' gilt:<br> | |||
S = f (0,5) <math>\cdot</math> 0,5 + f (1) <math>\cdot</math> 0,5 + .....f (4) <math>\cdot</math> 0,5 = 0,5 <math>\cdot</math>f(0,5) + f(1) + ...f (4) = 6,375 <br> | |||
Für den '''Flächeninhalt der Untersumme''' gilt:<br> | |||
s = f (0) <math>\cdot</math> 0,5 + f (0,5) <math>\cdot</math> 0,5 + .....f (3,5) <math>\cdot</math> 0,5 = 4,375 <br> | |||
'''Mittelwert: 5,375''' | |||
</popup> | |||
|Farbe= #557799 | |||
|Rahmen= 0 | |||
|Rahmenfarbe= #FFFFFF | |||
|Hintergrund= #FFFFFF | |||
|Icon= | |||
}} | |||
[[bild:Int_abb1.png|220px|right]] | [[bild:Int_abb1.png|220px|right]] | ||
Version vom 18. Februar 2020, 08:30 Uhr
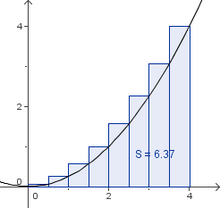
- Aufgabe 1: Gegeben ist die Funktion f(x) = 0.25 x².
- Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft.
- Berechne die zugehörige Ober- und Untersumme.
- Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an.
- Lösung:
<popup name="Lösung">
Wir zerlegen das [0;4] in 8 Teilintervalle. Jedes Teilintervall ist 0,5 breit.
Zu den x-Werten 0; 0,5; 1; 1,5;.....4 gehören die folgenden y-Werte:
x | 0 0,5 1 1,5 2 2,5 3 3,5 4 ----------------------------------------------------------- f(x)| 0 0,0625 0,25 0,5625 1 1,5625 2,25 3,0625 4
Für den Flächeninhalt der Obersumme gilt:
S = f (0,5) 0,5 + f (1) 0,5 + .....f (4) 0,5 = 0,5 f(0,5) + f(1) + ...f (4) = 6,375
Für den Flächeninhalt der Untersumme gilt:
s = f (0) 0,5 + f (0,5) 0,5 + .....f (3,5) 0,5 = 4,375
Mittelwert: 5,375 </popup>
- Aufgabe 2: Gegeben ist die Funktion f(x) = 0.5 x².
- Zerlege das Intervall [0;1] mit dem Schieberegler in gleichlange Teilintervalle und bestimme die zugehörige Ober- und Untersumme mit dem Applet.