6d 2024 25/Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 308: | Zeile 308: | ||
==28.03.2025: Hausaufgabe == | ==28.03.2025: Hausaufgabe == | ||
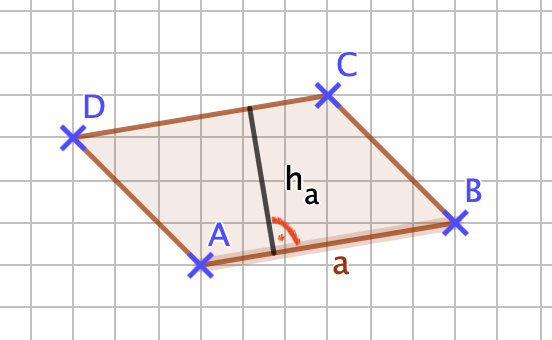
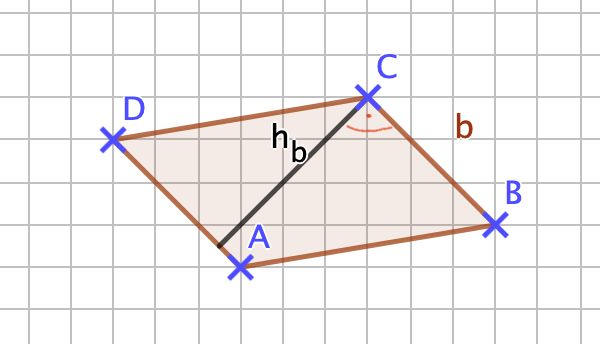
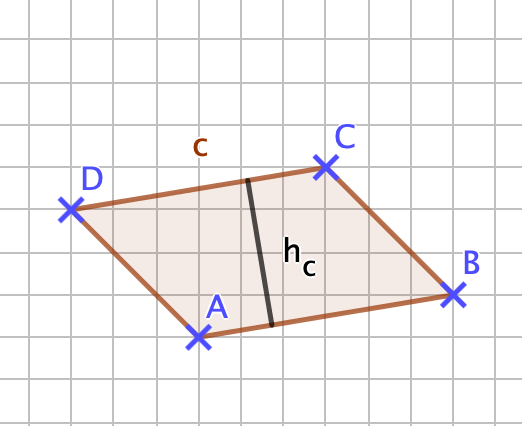
{{Box |1= Übung: |2= Bevor du startest wiederhole bitte für dich die Formel zur Berechnung des Flächeninhalts eines Parallelogramms und auch die Formel zur Berechnung seines Umfangs. | {{Box |1= Übung: |2= Bevor du startest wiederhole bitte für dich die Formel zur Berechnung des Flächeninhalts eines Parallelogramms und auch die Formel zur Berechnung seines Umfangs. <br> | ||
Bearbeite bitte im Buch S. 141/ 6! <br> | Bearbeite bitte im Buch S. 141/ 6! <br> | ||
| Zeile 324: | Zeile 324: | ||
'''Feststellung und Begründung:''' | '''Feststellung und Begründung:''' | ||
Unterschiede im Flächeninhalt entstehen aufgrund von Messungenauigkeiten. Eigentlich sollte bei jeder Messung und Rechnung immer der gleiche Flächeninhalt herauskommen, die Fläche des Parallelogramms verändert sich ja nicht.... |2=Zeile 4 Aufdecken|3=Verbergen}} | Unterschiede im Flächeninhalt entstehen aufgrund von Messungenauigkeiten. Eigentlich sollte bei jeder Messung und Rechnung immer der gleiche Flächeninhalt herauskommen, die Fläche des Parallelogramms verändert sich ja nicht.... |2=Zeile 4 Aufdecken|3=Verbergen}} | ||
|3= Üben}} | |||
{{Box |1= Übung: |2= Bearbeite B. S. 142/ 12 b), c)! <br> Vergiss nicht die Anwendungsmöglichkeit einer Umkehrrechnung... | |||
{{Lösung versteckt |1= '''Lösung der Aufgaben:''' <br> | |||
'''b)''' <br> | |||
h = 5,2 cm und A = 22,36 cm² <br> Löse mit der Umkehraufgabe: <br> | |||
<math> g= A \div h = 22,36 cm^2 \div 5,2 cm = 223,6 cm^2 \div 52 cm = 4,3 cm </math> <br> Vergiss bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! | |||
'''c)''' <br> | |||
Am besten du rechnest beide Größen sofort in dieselbe Einheit um! <br> g = 150 cm und A = 9,75 m² = 975 dm² = 97500 cm² <br> Löse mit der Umkehraufgabe: <br> | |||
<math> h= A \div g = 97500 cm^2 \div 150 cm = 650 cm = 6,5 m </math> <br> Vergiss auch hier bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! | |||
|2= Lösung anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |3= Üben}} | ||
Version vom 25. März 2025, 16:14 Uhr
31.01.2025: Übungen zu Multiplizieren mit Stufenzahlen und Dividieren durch Stufenzahlen
Zur Vorbereitung zu Hause auf die kommende Stunde - Multiplizieren von Dezimalbrüchen
03.02.25: Weiter geht es mit dem Multiplizieren von Dezimalbrüchen
14.02.2025: Dividieren von Dezimalbrüchen und Hausaufgabe zum Multiplizieren von Dezimalbrüchen
18.02.2025: Hausaufgabe
10.03.2025: Hausaufgabe - Zur Wiederholung
25.03.2025: Hausaufgabe zu Parallelogramm und Wiederholung zu Einheiten