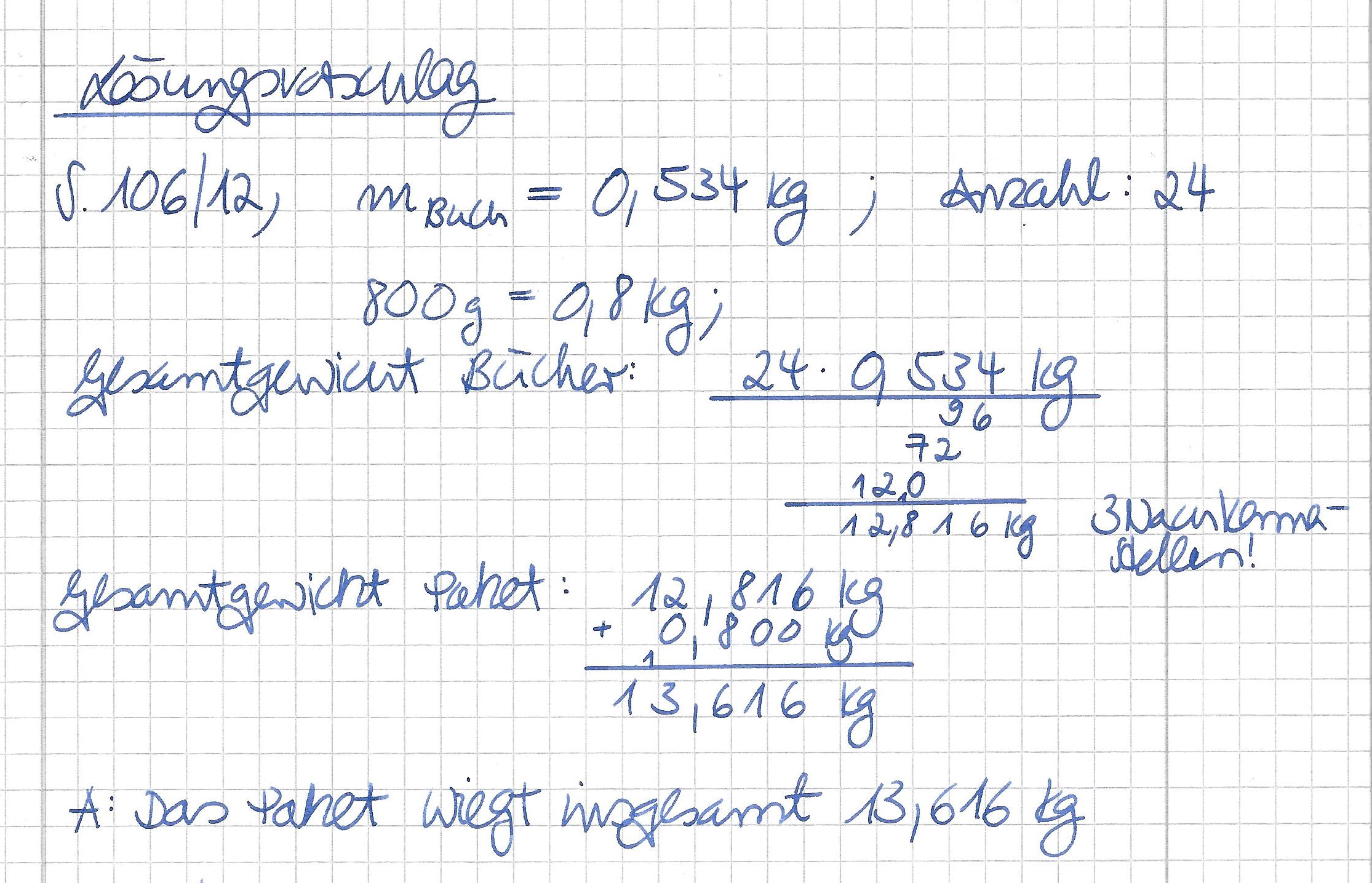6d 2024 25/Mathematik

31.01.2025: Übungen zu Multiplizieren mit Stufenzahlen und Dividieren durch Stufenzahlen

Test:

Nun kannst du testen, ob du das Multiplizieren mit einer Stufenzahl und das Dividieren durch eine Stufenzahl verstanden hast.
25; 2,5; 250; 0,25 sind die möglichen Ergebnisse - deine Aufgabe hier ist es die Ergebnisse nacheinander anzuwählen (sie leuchten dann blau) und jeweils alle Puzzleteile anzuklicken, bei denen das ausgewählte Ergebnis herauskommt.

Übung 1:

Bearbeite bitte im Buch S. 102/ 3 - jedoch nur für Stellenwert der Ziffer 7!
Verbessere deine Lösung in ROT!

Lösung Aufgabe 3 anzeigen

a) Multipliziert mit:

• 10: Zehntel
• 100: Einer
• 1000: Zehner
• 10000: Hunderter
  

b) Dividiert durch:

• 10: Tausendstel
• 100: Zehntausendstel
• 1000: Hunderttausendstel
• 10000: Millionstel

Übung 2:

Bearbeite bitte im Buch S. 102/ 4!
Verbessere deine Lösung in ROT!

Lösung Aufgabe 4 anzeigen

a) 0,024
b) 3,6
c) 71
d) 0,086
e) 0,00371
f) 0,00065

Anmerkung zu Teilaufgabe 4 f):
Ein Hunderttausendstel von 65, d.h. man rechnet 65 (man könnte für 65 auch 65,0 notieren) geteilt durch 100000 - das bedeutet "man geht" 5 Stellen nach links... um dies tun zu können, muss man zunächst auf der linken Seite von 65 Nullen ergänzen, d.h. man rechnet im Endeffekt 000065: 100000 = 0,00065 und schiebt das (nicht vorhandene) Komma von rechts eine Stelle nach links zwischen die 6 und die 5, dann eine zweite Stelle nach links zwischen 0 und 6 und so weiter, bis man alle 5 Stellen "gegangen ist"... und erhält dann als Ergebnis 0,00065

Übung 3:

Bearbeite bitte im Buch S. 102/ 5!
Verbessere deine Lösung in ROT!

Lösung Aufgabe 5 anzeigen

a) $60 mm \div 1000 = 0060 mm : 1000 = 0,06 mm$
Anmerkung: Man verschiebt das Komma drei Stellen links.
Antwortsatz: Das menschliche Haar ist in Wirklichkeit 0,06 mm dick.

b) $0,005 mm \cdot 1000 = 5 mm$
Anmerkung: Man verschiebt das Komma drei Stellen nach rechts.
Antwortsatz: Der Spinnwebfaden erscheint 5 mm dick.

Übung 4:

Bearbeite bitte im Buch S. 102/7 b)!
Verbessere deine Lösung in ROT!

Lösung Aufgabe 7 anzeigen

• $0,933 \div 10 = 0,0933$
• $0,933 \cdot 100 = 93,3$
• $0,0933 \cdot 1000 = 93,3$
• $930 \div 10000 = 0,093$

Hausaufgabe:

Bearbeite B. S. 102/ 2 - hier geht es um Kopfrechnen...

Wenn du magst, berechne doch die Aufgaben am Telefon gemeinsam mit jemanden aus deiner Klasse...
ODER
Berechne die Aufgaben alleine und besprich diese im Anschluss mit jemanden aus deiner Klasse z.B. am Telefon...
Gemeinsam über Mathe reden hilft ungemein beim Verständnis.
ODER
Berechne alleine die Aufgaben...

Am Montag werden die Aufgaben im Unterricht besprochen.... Also vergiss bitte nicht Hausaufgaben zu machen :-)

Zur Vorbereitung zu Hause auf die kommende Stunde - Multiplizieren von Dezimalbrüchen

Neu:

Nicht verrückt machen, wenn du Schriftlich Multiplizieren und auch noch zählen kannst, sollte das Multiplizieren von Dezimalbrüchen kein Problem werden.
Notiere dir zunächst die Überschrift "Multiplizieren von Dezimalbrüchen" mit dem heutigen Datum in dein Heft!

Sieh dir nun das folgende Video aufmerksam an!

Multiplizieren von Dezimalbrüchen:

Dezimalbruch multiplizieren | Kommazahlen multiplizieren - einfach erklärt | Lehrerschmidt

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Zur Kontrolle:

Nun bist du an der Reihe! Berechne nun nochmal alleine die beiden Aufgaben aus dem Video!

• Berechne $8,3 \cdot 1,4$!

Aufdecken

$= 11,62$
WICHTIG: Die Zahl 8,3 hat eine Nachkommastelle, ebenso die Zahl 1,4.
Somit hat das Ergebnis der Multiplikation zwei Nachkommastellen, denn "1 Nachkommastelle + 1 Nachkommastelle = 2 Nachkommastellen"!

• Berechne $31,4 \cdot 1,21$!

Aufdecken

$= 37,994$
WICHTIG: Die Zahl 31,4 hat eine Nachkommastelle, die Zahl 1,21 hat zwei Nachkommastellen.
Da "1 Nachkommastelle + 2 Nachkommastellen = 3 Nachkommastellen", hat das Ergebnis der Multiplikation drei Nachkommastellen...

Falls nun noch etwas unklar sein sollte oder deine Lösungen so ganz anders als meine, dann schau dir bitte nochmal obiges Video an und rechne Schritt für Schritt mit Lehrer Schmidt ;-)

Und alles klar?

Notiere bitte noch folgenden Merksatz in dein Heft!

Merke: Regel für die Multiplikation von Dezimalbrüchen

1. Multipliziere zunächst so, als wäre kein Komma vorhanden - Stichwort: schriftlich Multiplizieren!
2. Setze dann im Ergebnis das Komma so, dass rechts vom Komma so viele Zahlen stehen, wie die beiden Faktoren zusammen nach dem Komma haben!

03.02.25: Weiter geht es mit dem Multiplizieren von Dezimalbrüchen

Zur Vertiefung:

Berechne folgende Aufgaben!

• B.S.106/ 19 a): Berechne $30,8 \cdot 0,29$!

Aufdecken

$=8,932$
WICHTIG: Berechne zunächst schriftlich $308 \cdot 29$. Das Ergebnis hier ist 8932.
Die Zahl 30,8 hat eine Nachkommastelle, die Zahl 0,29 hat zwei Nachkommastellen.
Somit hat das Ergebnis der Multiplikation drei Nachkommastellen, denn "1 Nachkommastelle + 2 Nachkommastellen = 3 Nachkommastellen"!

• B.S.106/ 19 e): Berechne $9,93 \cdot 0,19$!

Aufdecken

$= 1,8867$
WICHTIG: Berechne zunächst schriftlich $993 \cdot 19$. Das Ergebnis hier ist 18867.
Die Zahl 9,93 hat zwei Nachkommastellen, die Zahl 0,19 hat zwei Nachkommastellen.
Da "2 Nachkommastellen + 2 Nachkommastellen = 4 Nachkommastellen", hat das Ergebnis der Multiplikation vier Nachkommastellen...

• B.S.106/ 19 l): Berechne $0,508 \cdot 53,6$!

Aufdecken

$= 27,2288$
WICHTIG: Berechne zunächst schriftlich $508 \cdot 536$. Das Ergebnis hier ist 272288.
Die Zahl 0,508 hat drei Nachkommastellen, die Zahl 53,6 hat eine Nachkommastelle.
Da "3 Nachkommastellen + 1 Nachkommastelle = 4 Nachkommastellen", hat das Ergebnis der Multiplikation vier Nachkommastellen...

Übung:

Bearbeite bitte folgende Aufgaben im Schulheft: B. S. 106/ 12, 15 und 17 b)

Lösung Aufgabe 12 anzeigen

Lösung Aufgabe 15 anzeigen

Lösung Aufgabe 17 b) anzeigen

Zur Vertiefung:

Notiere in der Lösungszeile nur die Zahl, die in die gelb markierte Lücke notiert werden muss, beachte dabei auch die "Gemerkten".

Nun noch etwas Kopfrechnen...:

Kommaverschiebung für Produkte:

Bearbeite bitte B. S. 104/ 2! Übertrage bitte auch den roten Kasten als Merksatz in dein Schulheft während du die Aufgabe bearbeitest !

Lösung Aufgabe 2 anzeigen

Übung:

Bearbeite bitte B. S. 105/ 7 b), c) und 11!

Lösung Aufgabe 7 und 11 anzeigen

FREIWILLIG:

Falls du noch Energie hast, kannst du hiermit nochmal das Multiplizieren von Dezimalbrüchen üben...nimm dir bitte für Nebenrechnungen einen Stift und dein Heft zur Hand, das Erraten der Lösungen bringt leider nicht sehr viel...

14.02.2025: Dividieren von Dezimalbrüchen und Hausaufgabe zum Multiplizieren von Dezimalbrüchen

Zur Wiederholung und Erinnerung an die 5. Klasse:

Berechne $5472 \div 12$ schriftlich!

Aufdecken

$5472 \div 12 = 456$

Neu:

Heute geht es los mit dem Dividieren von Dezimalbrüchen, zunächst mit dem Dividieren von Dezimalbrüchen durch eine natürliche Zahl. Bevor du mit dem Video startest, notiere dir bitte die beiden fett gedruckten Sätze als Überschrift in dein Heft!
Sieh dir nun zunächst folgendes Video aufmerksam an! Notiere dir zeitgleich die drei Aufgaben, die im Video berechnet werden auf einem Schmierzettel, damit du diese im Anschluss an das Video noch einmal alleine berechnen kannst...

FÜR DIE WIEDERHOLUNG ZU HAUSE: Dividieren von Dezimalbrüchen:

Dezimalbruch dividieren | Kommazahl divideren - einfach erklärt | Lehrerschmidt

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Zum Einstieg:

Wir berechnen gemeinsam ein paar Beispiele. Zu Hause kannst du die Vorgehensweise beim "Dividieren von Dezimalbrüchen durch eine natürliche Zahl" nochmals mit dem Video von Lehrer Schmidt vertiefen; unsere Einstiegsbeispiele sollten dir bereits bekannt vorkommen ;-)

Aufdecken

$25,8 \div 6 = 4,3$
$0,049 \div 7 = 0,007$
$37,65 \div 12 = 3,1375$

Und alles klar?

Notiere bitte folgenden Merksatz in dein Heft!

Merke: Division eines Dezimalbruchs durch eine natürliche Zahl

1. Dividiere den Dezimalbruch stellenweise durch die natürliche Zahl, so wie du es von der Division einer natürlichen Zahl durch eine natürliche Zahl bereits gewohnt bist.
2. Wichtig: Sobald du bei der Berechnung das Komma "überschreitest", setze auch im Ergebnis ein Komma!
3. Eventuell ist es nötig, um die Aufgabe komplett berechnen zu können, zum Ende des Rechenvorgangs beim Dezimalbruch noch nicht geschriebene Endnullen zu ergänzen.

Lies dir diesen Merksatz nun noch einmal in Ruhe durch und verinnerliche die Vorgehensweise bei der Division eines Dezimalbruchs durch eine natürliche Zahl bevor es mit Übungen weiter geht!

Zur Übung:

Kopfrechnen - Schlage das Buch S. 110/ 2 auf, stelle dir einen Timer auf 5 Minuten und versuche in der Zeit so viele Aufgaben wie möglich zu berechnen.
Notiere dir jeweils dein Ergebnis, damit du deine Lösung mit meiner im Anschluss vergleichen kannst.... Ich hoffe du bist schon zurecht gekommen!

Aufdecken

a) 0,7; b) 0,8; c) 0,8; d) 1,8; e) 2,4; f) 3,25; g) 0,16; h) 0,04; i) 1,2; j) 1,2; k) 0,22; l) 0,17;

Zur Übung:

Nun bestimmt etwas schwieriger für dich: Berechne B. S. 110/ 5 a), b), c), d), g) und freiwillig e)!
Versuche konzentriert jede Aufgabe zu berechnen, wende dein neu erworbenes Wissen an und versuche ruhig zu bleiben, dann kommst du sicher ans Ziel!
Mit diesen Aufgaben sollst du Rechenroutine bekommen... Bitte bei Teilaufgabe e), falls du diese freiwillig versuchst, nach spätestens 5 Minuten aufhören!
Verbessere bitte deinen Lösungsvorschlag!
Falls dein Ergebnis ein anderes sein sollte, dann vergleiche bitte deine Lösung Schritt für Schritt mit der von mir!

Lösung Aufgabe 5 anzeigen

HAUSAUFGABE - Zur Wiederholung und Vertiefung:

Damit du das Multiplizieren von Dezimalbrüchen nicht so schnell vergisst, wirst du es mit folgenden Aufgaben zum einen wiederholen und zum anderen weiter vertiefen.
Parat haben solltest du hierfür auch das Wissen zu Potenzen und die Rechenvorschrift "von links nach rechts"...
Berechne nun Buch S. 107/ 20 a), b), c) und S. 107/ 22 e), f)!

B. S. 107/ 20 a), b), c) Aufdecken

Tipp: Berechne hier Schritt für Schritt von "links nach rechts"! Vergiss die Zwischenschritte nicht!
a)     1,4·2,6·3 = 3,64·3 = 10,92

b)    4,9·7·1,5 = 34,3·1,5 = 51,45

c)     0,62·0,25·17,8 = 0,155·17,8 = 2,759

B. S. 107/ 22 e), f) Aufdecken

e) 1,2³ = 1,2·1,2·1,2 = 1,44·1,2 = 1,728

f) 2,5³ = 2,5·2,5·2,5 = 6,25·2,5 = 15,625

18.02.2025: Hausaufgabe

Hausaufgabe

WICHTIG: Vergiss nicht die Lösung der Aufgabenpaare im Schulheft zu berechnen/ zu notieren, nachdem du diese zugeordnet hast!

Aufdecken

Die Aufgabenpaare inklusive zugehöriger Lösung:

• 32 : 800 = 0,32 : 8 = 0,04
• 32 : 8 = 3,2 : 0,8 = 4
• 3200 : 8 = 32 : 0,08 = 400
• 30 : 6 = 0,3 : 0,06 = 5
• 300: 6 = 3 : 0,06 = 50
• 96 : 12 = 0,96 : 0,12 = 8
  

Die links notierte Rechenaufgabe ist die, die man einfacher berechnen kann.

Ausblick:

Du hast es dir sicher schon gedacht, auch beim Rechnen mit Dezimalzahlen gelten nach wie vor die Rechenregeln "Klammern zuerst", "Potenz vor Punkt vor Strich", "von links nach rechts" und natürlich können Dezimalbrüche auch in Textaufgaben vorkommen...
Berechne die jeweilige Aufgabe im Kopf! Mit diesen Aufgaben kannst du testen, ob du Rechengesetze richtig anwendest und Textaufgaben richtig verstehst... Wenn du magst, kannst du dir hierbei freiwillig die jeweilige Aufgabe inklusive ihrer Lösung kurz ins Schulheft notieren.
Anmerkung: Pickerl = Sticker

Zum Abschluss:

Noch etwas Kopfrechnen - Schlage das Buch S. 114/ 4 auf und berechne nacheinander die Aufgaben im Kopf.
Notiere dir jeweils dein Ergebnis, damit du deine Lösung mit meiner im Anschluss vergleichen kannst....

Aufdecken

a) "32 : 8" = 4; b) "56 : 7" = 8; c) "30 : 6" = 5; d) "40 : 5" = 8;
e) "50 : 25" = 2; f) "2000 : 2" = 1000; g) "15 : 3" = 5; h) "30 : 6" = 5;
i) "200 : 4" = 50; j) "64: 8" = 8; k) "250 : 2" = 125; l) "1800 : 6" = 300;

FREIWILLIG - Zur Vertiefung:

Potenzen und Dezimalbrüche...
Berechne jeweils und ordne das richtige Ergebnis zu. Achte hierbei auf die richtige Anzahl der Nachkommastellen!

10.03.2025: Hausaufgabe - Zur Wiederholung

Wiederholung:

Fasse mündlich noch einmal für dich zusammen, was ein endlicher Dezimalbruch ist und wie er entsteht!
Definiere, was ein periodischer Dezimalbruch ist, wie ist hierbei die Notation!
Lerne den Zusammenhang zwischen Brüchen mit Nenner 9 und ihren periodischen Dezimalbrüchen!

LERNE!! - Brüche mit Nenner 9:

Bitte keine Panik, das ist nicht so viel, wie es auf den ersten Blick wirkt, du erkennst sicherlich ein Schema beim Lernen und denke bitte immer an die Möglichkeit des Kürzens, das erklärt doch auch so einiges...

Merke anzeigen

Merke dir:

• ${1 \over 9} = 0,\bar{1}$; "null Komma Periode eins"
  
• ${2 \over 9} = 0,\bar{2}$; "null Komma Periode zwei"
  
• ${3 \over 9} = {1 \over 3} = 0,\overline{3}$; "null Komma Periode drei"
  
• ${4 \over 9} = 0,\bar{4}$; "null Komma Periode vier"
  
• ${5 \over 9} = 0,\bar{5}$; "null Komma Periode fünf"
  
• ${6 \over 9} = {2 \over 3} = 0,\overline{6}$; "null Komma Periode sechs"
  
• ${7 \over 9} = 0,\bar{7}$; "null Komma Periode sieben"
  
• ${8 \over 9 }= 0,\bar{8}$; "null Komma Periode acht"
  
• ${9 \over 9} = 0,\bar{9} = 1$
  

Test:

Zum Überprüfen und weiteren Vertiefen deines gelernten Wissens kannst du hier freiwillig noch einmal Paare von Brüchen und Dezimalbrüchen passend zuordnen. Mit der folgenden LearningApp hast du die Möglichkeit zu testen, ob du besondere Brüche und ihre zugehörigen Dezimalzahlen bereits gut genug gelernt hast. Viel Freude dabei!

Test:

Zur Wiederholung und Vertiefung: Endlich oder unendlicher Bruch? Sortiere jeweils zu! Kürzen bzw. Erweitern auf 10, 100, 1000, 10000, ... kann dir dabei helfen endliche Brüche "herauszuangeln..."

25.03.2025: Hausaufgabe zu Parallelogramm und Wiederholung zu Einheiten

Erinnerung:

Zur Berechnung des Flächeninhalts eines Parallelogramms benötigt man, wie du weißt, die Höhen im Parallelogramm. Mit folgender Darstellung kannst du erkennen, wie die Höhe im Parallelogramm dargestellt wird. Verschiebe die blauen Punkte des Parallelogramms mit deiner Maus und beobachte dabei, wann sich die Höhen innerhalb bzw. außerhalb des Parallelogramms befinden und wie man diese einzeichnet.

Hinweis:

Aufdecken

Höhen im Parallelogramm
Unter den Höhen eines Parallelogramms versteht man die Abstände der zueinander parallelen Seiten des Parallelogramms. Ein Parallelogramm hat zwei Höhen.
Man zeichnet die Höhe, indem man eine Strecke rechtwinklig zu einer Seite zeichnest und diese mit der dazu parallelen Seite verbindest.

FREIWILLIG - Einzeichnen der Höhen - 1:

Parallelogramm Höhen einzeichnen 1

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

FREIWILLIG - Einzeichnen der Höhen - 2:

Parallelogramm Höhen einzeichnen 2

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung - Berechnung des Flächeninhalts von Parallelogrammen:

Nun darfst du selbst die Höhe suchen.... und hoffentlich finden! Falls das noch nicht so gut klappen sollte, nochmal der Hinweis auf die freiwilligen Videos vorab zum Zeichnen der Höhen beim Parallelogramm.

Zur Wiederholung:

Zum Abschluss der heutigen Hausaufgabe noch etwas Umrechnen von Einheiten - zunächst Längeneinheiten... Du musst hier nicht alle Aufgaben bearbeiten, sollten dir die einfachen zu einfach sein, dann lass sie bitte einfach weg, die zu "schwieriger" sind jedoch Pflicht!
Zum Reinkommen in das Umrechnen von Einheiten können die "einfachen" Aufgaben aber auch hilfreich sein, dies entscheidest du aber vollkommen selbstständig, je nachdem, wie gut du dich noch an das Umrechnen von Einheiten erinnern kannst!

Zur Wiederholung:

Und nun noch etwas Umrechnen von Einheiten - ein paar Flächeneinheiten...

28.03.2025: Hausaufgabe

Übung:

Bevor du startest wiederhole bitte für dich die Formel zur Berechnung des Flächeninhalts eines Parallelogramms und auch die Formel zur Berechnung seines Umfangs. Solltest du feststellen, dass noch etwas unklar ist, dann schau dir bitte entsprechend das Erklärvideo der vergangenen Stunde an. Danke!
Wenn alles klar ist, dann geht's auch schon los....

Bearbeite bitte im Buch S. 141/ 6!
Berechne Zeile für Zeile und verbessere immer direkt im Anschluss deine Lösung mit dem folgenden Lösungsvorschlag.
Lass dich nicht irritieren, du fertigst im Heft nur eine Skizze des Parallelogramms an - hier ist für jede Zeile eine Skizze angefügt, dies dient der besseren Übersichtlichkeit und Nachvollziehbarkeit der Lösung.

Zeile 1 Aufdecken

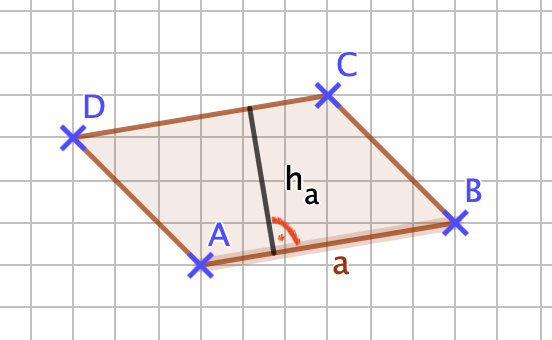
Wenn du richtig gezeichnet hast, dann müsste die Seite $\overline{AB} = a$ ca. 3cm sein und die zugehörige Höhe ca. 1,7cm.
Der Flächeninhalt ist dann: A=3cm•1,7cm=5,1cm²

Sollten deine Werte um 1-2mm abweichen ist das kein Problem.

Zeile 2 Aufdecken

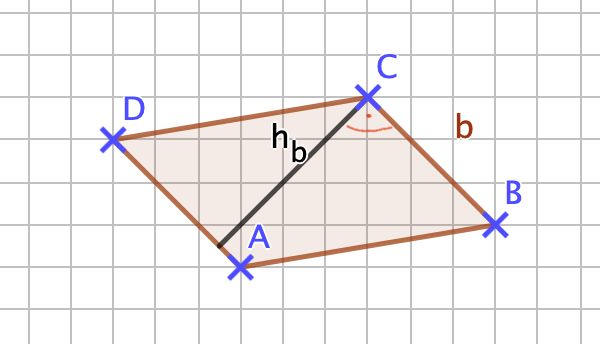
Die Länge der Seite $\overline{BC} = b$ ist ca. 2,1cm die zugehörige Höhe ist ca. 2,5cm.
Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². Sollten deine Werte um 1-2mm abweichen ist das kein Problem.

Zeile 3 Aufdecken

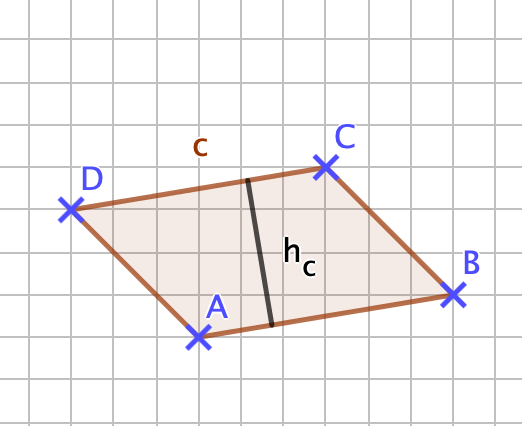
Die Länge der Seite $\overline{CD} = c$ ist ca. 3cm, c =a! Die zugehörige Höhe ist dann ebenfalls, wie auch die Höhe zur Seite a, ca. 1,7cm.
Mit diesen Werten kommt man auf einen Flächeninhalt von 5,1cm².

Zeile 4 Aufdecken

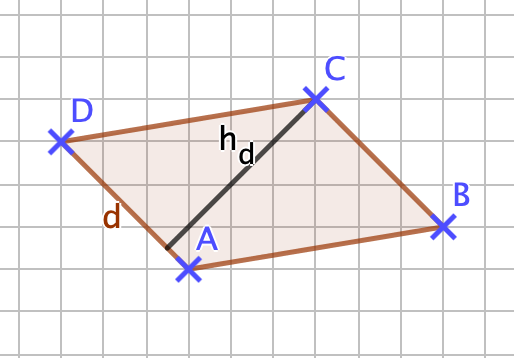
Die Länge der Seite $\overline{DA} = d$ ist ca. 2,1cm, d = b! Die zugehörige Höhe ist, wie auch die Höhe zur Seite b, ca. 2,5cm. Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm².

Feststellung und Begründung:

Unterschiede im Flächeninhalt entstehen aufgrund von Messungenauigkeiten. Eigentlich sollte bei jeder Messung und Rechnung immer der gleiche Flächeninhalt herauskommen, die Fläche des Parallelogramms verändert sich ja nicht....