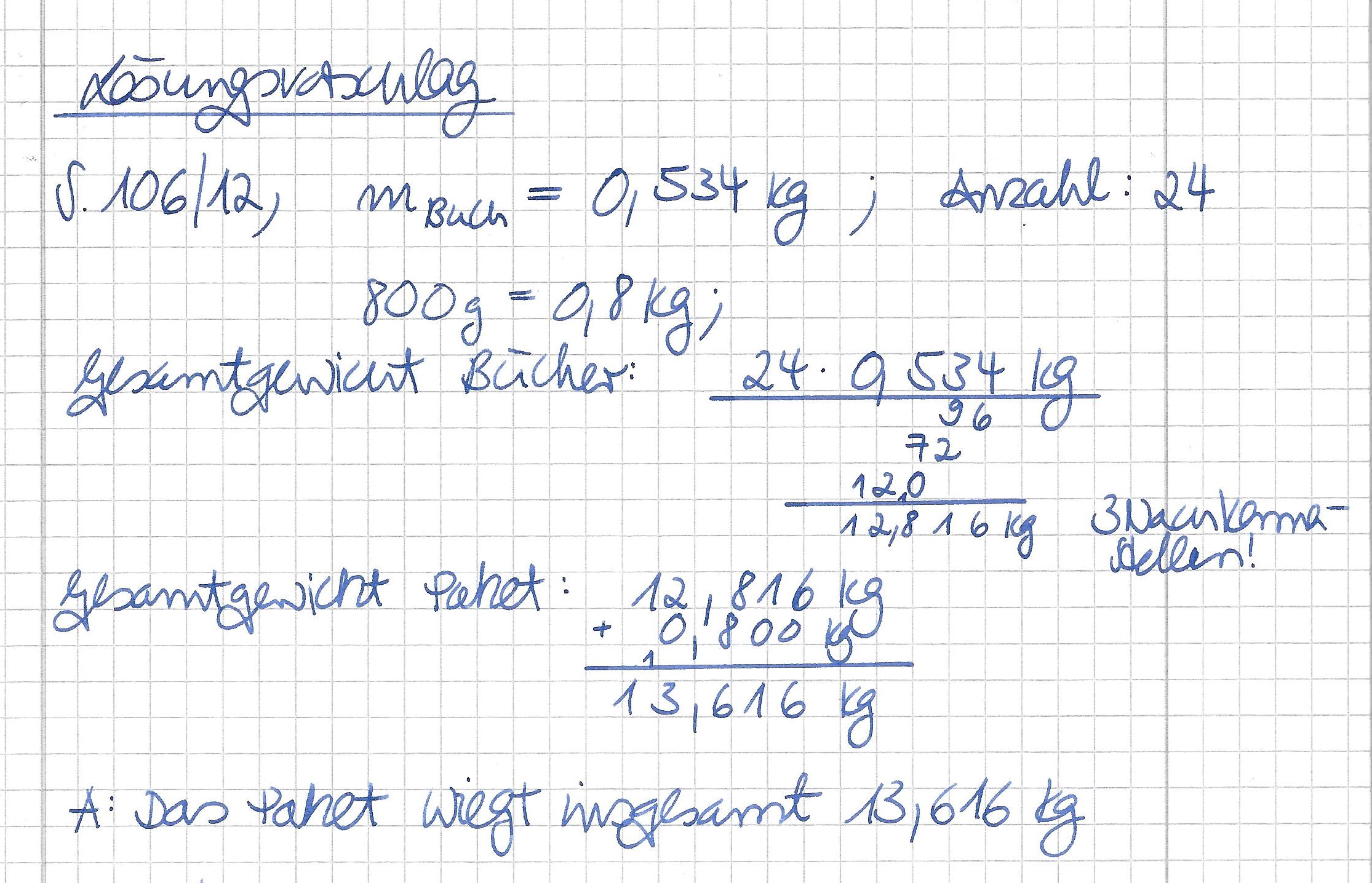6d 2024 25/Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 162: | Zeile 162: | ||
{{Box|1= Neu: |2= Heute geht es los mit dem '''Dividieren von Dezimalbrüchen''', zunächst mit dem '''Dividieren von Dezimalbrüchen durch eine natürliche Zahl'''. Bevor du mit dem Video startest, notiere dir bitte die beiden fett gedruckten Sätze als Überschrift in dein Heft! <br> Sieh dir nun zunächst folgendes Video aufmerksam an! Notiere dir zeitgleich die drei Aufgaben, die im Video berechnet werden auf einem Schmierzettel, damit du diese im Anschluss an das Video noch einmal alleine berechnen kannst...| 3= Arbeitsmethode}} | {{Box|1= Neu: |2= Heute geht es los mit dem '''Dividieren von Dezimalbrüchen''', zunächst mit dem '''Dividieren von Dezimalbrüchen durch eine natürliche Zahl'''. Bevor du mit dem Video startest, notiere dir bitte die beiden fett gedruckten Sätze als Überschrift in dein Heft! <br> Sieh dir nun zunächst folgendes Video aufmerksam an! Notiere dir zeitgleich die drei Aufgaben, die im Video berechnet werden auf einem Schmierzettel, damit du diese im Anschluss an das Video noch einmal alleine berechnen kannst...| 3= Arbeitsmethode}} | ||
{{Box| Dividieren von Dezimalbrüchen: |{{#ev:youtube|4IosoF-ldMs}} | Hervorhebung1}} | {{Box| FÜR DIE WIEDERHOLUNG ZU HAUSE: Dividieren von Dezimalbrüchen: |{{#ev:youtube|4IosoF-ldMs}} | Hervorhebung1}} | ||
{{Box |1= | {{Box |1= Zum Einstieg: |2= Wir berechnen gemeinsam ein paar Beispiele. Zu Hause kannst du die Vorgehensweise beim "Dividieren von Dezimalbrüchen durch eine natürliche Zahl" nochmals mit dem Video von Lehrer Schmidt vertiefen - unsere Einstiegsbeispiele werden dir sollten dir bereits bekannt vorkommen ;-) | ||
{{Lösung versteckt|1= <math> 25,8 \div 6 = 4,3 </math> <br> <math> 0,049 \div 7 = 0,007 </math> <br> <math> 37,65 \div 12 = 3,1375 </math> |2= Aufdecken|3=Verbergen}} | {{Lösung versteckt|1= <math> 25,8 \div 6 = 4,3 </math> <br> <math> 0,049 \div 7 = 0,007 </math> <br> <math> 37,65 \div 12 = 3,1375 </math> |2= Aufdecken|3=Verbergen}} | ||
|3= Üben}} | |3= Üben}} | ||
| Zeile 199: | Zeile 196: | ||
{{Box |1= Zur Wiederholung und Vertiefung: |2= Damit du das Multiplizieren von Dezimalbrüchen nicht so schnell vergisst, | {{Box |1= HAUSAUFGABE - Zur Wiederholung und Vertiefung: |2= Damit du das Multiplizieren von Dezimalbrüchen nicht so schnell vergisst, wirst du es mit folgenden Aufgaben zum einen wiederholen und zum anderen weiter vertiefen. <br> Parat haben solltest du hierfür auch das Wissen zu Potenzen und die Rechenvorschrift "von links nach rechts"... <br> Berechne nun Buch S. 107/ 20 a), b), c) und S. 107/ 22/ a), e), f)! | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Version vom 11. Februar 2025, 18:58 Uhr
31.01.2025: Übungen zu Multiplizieren mit Stufenzahlen und Dividieren durch Stufenzahlen
Zur Vorbereitung zu Hause auf die kommende Stunde - Multiplizieren von Dezimalbrüchen
03.02.25: Weiter geht es mit dem Multiplizieren von Dezimalbrüchen
14.02.2025: Dividieren von Dezimalbrüchen und Hausaufgabe zum Multiplizieren von Dezimalbrüchen