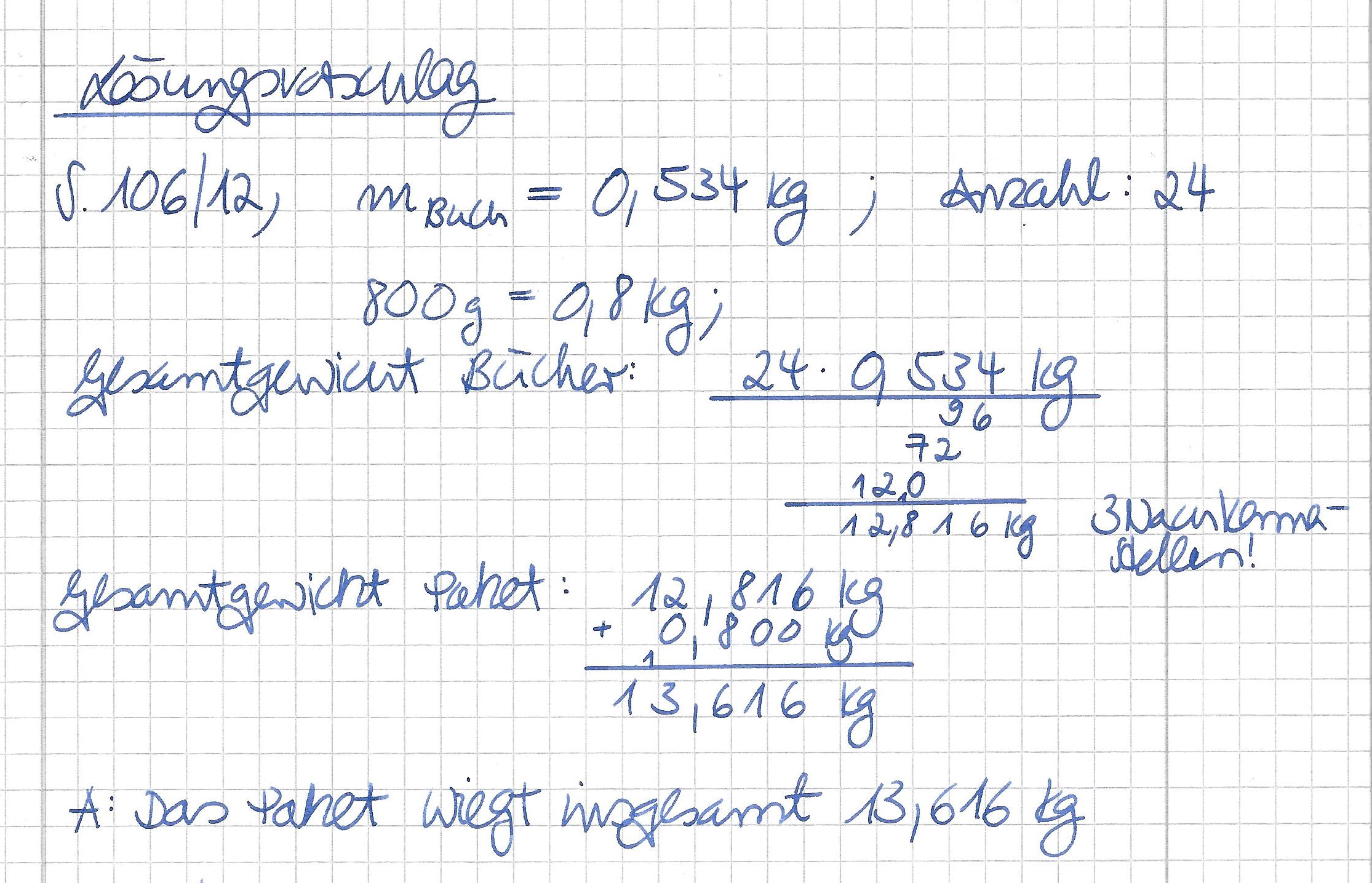6d 2024 25/Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (33 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 305: | Zeile 305: | ||
{{Box |1= Zur Wiederholung:|2= Und nun noch etwas Umrechnen von Einheiten - ein paar Flächeneinheiten... <br> {{LearningApp|app=pfhyzuzvn21|width=100%|height=700px}} <br> |3= Arbeitsmethode}} | {{Box |1= Zur Wiederholung:|2= Und nun noch etwas Umrechnen von Einheiten - ein paar Flächeneinheiten... <br> {{LearningApp|app=pfhyzuzvn21|width=100%|height=700px}} <br> |3= Arbeitsmethode}} | ||
=10. | |||
=28.03.2025: Hausaufgabe = | |||
{{Box |1= Übung: |2= Bevor du startest wiederhole bitte für dich die Formel zur Berechnung des Flächeninhalts eines Parallelogramms und auch die Formel zur Berechnung seines Umfangs. <br> | |||
Bearbeite bitte im Buch S. 141/ 6! <br> | |||
Berechne Zeile für Zeile und verbessere immer direkt im Anschluss deine Lösung mit dem folgenden Lösungsvorschlag. <br> Lass dich nicht irritieren, du fertigst im Heft nur eine Skizze des Parallelogramms an - hier ist für jede Zeile eine Skizze angefügt, dies dient der besseren Übersichtlichkeit und Nachvollziehbarkeit der Lösung. | |||
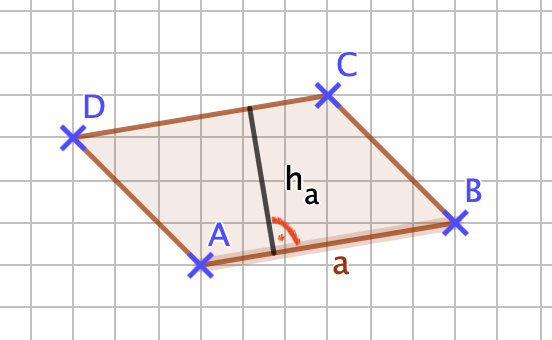
{{Lösung versteckt|1=[[Datei:141-6-1.png]]<br>Wenn du richtig gezeichnet hast, dann müsste die Seite <math>\overline{AB} = a </math> ca. 3cm sein und die zugehörige Höhe ca. 1,7cm. <br> Der Flächeninhalt ist dann: A=3cm•1,7cm=5,1cm² <br> | |||
Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 1 Aufdecken|3=Verbergen}} | |||
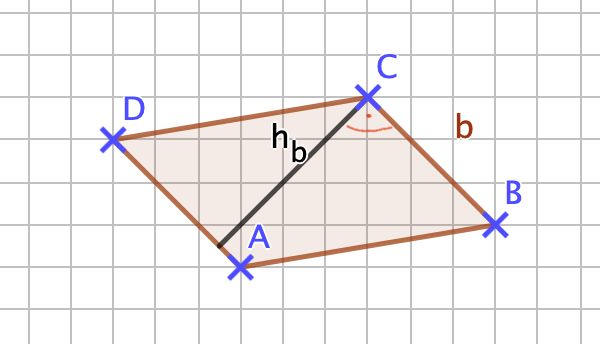
{{Lösung versteckt|1=[[Datei:141-6-2.png]]<br>Die Länge der Seite <math> \overline{BC} = b </math> ist ca. 2,1cm die zugehörige Höhe ist ca. 2,5cm. <br> Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 2 Aufdecken|3=Verbergen}} | |||
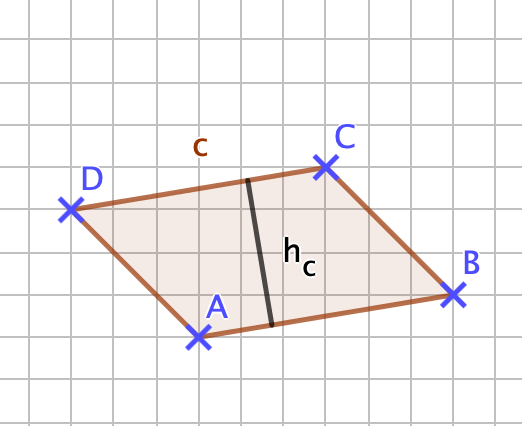
{{Lösung versteckt|1=[[Datei:141-6-4.png]]<br>Die Länge der Seite <math> \overline{CD} = c </math> ist ca. 3cm, c =a! Die zugehörige Höhe ist dann ebenfalls, wie auch die Höhe zur Seite a, ca. 1,7cm. <br> Mit diesen Werten kommt man auf einen Flächeninhalt von 5,1cm². |2=Zeile 3 Aufdecken|3=Verbergen}} | |||
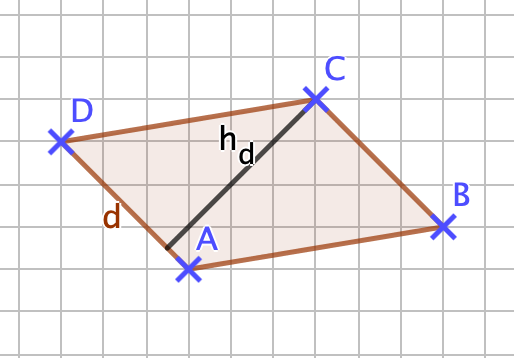
{{Lösung versteckt|1=[[Datei:141-6-3.png]]<br>Die Länge der Seite <math> \overline{DA} = d </math> ist ca. 2,1cm, d = b! Die zugehörige Höhe ist, wie auch die Höhe zur Seite b, ca. 2,5cm. Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². <br> | |||
'''Feststellung und Begründung:''' | |||
Unterschiede im Flächeninhalt entstehen aufgrund von Messungenauigkeiten. Eigentlich sollte bei jeder Messung und Rechnung immer der gleiche Flächeninhalt herauskommen, die Fläche des Parallelogramms verändert sich ja nicht.... |2=Zeile 4 Aufdecken|3=Verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Übung: |2= Bearbeite B. S. 142/ 12 b), c)! <br> Vergiss nicht die Anwendungsmöglichkeit einer Umkehrrechnung... | |||
{{Lösung versteckt |1= '''Lösung der Aufgaben:''' <br> | |||
'''b)''' <br> | |||
h = 5,2 cm und A = 22,36 cm² <br> Löse mit der Umkehraufgabe: <br> | |||
<math> g= A \div h = 22,36 cm^2 \div 5,2 cm = 223,6 cm^2 \div 52 cm = 4,3 cm </math> <br> Vergiss bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! | |||
'''c)''' <br> | |||
Am besten du rechnest beide Größen sofort in dieselbe Einheit um! <br> g = 150 cm und A = 9,75 m² = 975 dm² = 97500 cm² <br> Löse mit der Umkehraufgabe: <br> | |||
<math> h= A \div g = 97500 cm^2 \div 150 cm = 650 cm = 6,5 m </math> <br> Vergiss auch hier bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! | |||
|2= Lösung anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
=13.05.2025: Übungen zu rationalen Zahlen= | |||
{{Box|1=Zur Wiederholung: |2= Gehst du auf dem Zahlenstrahl nach links oder rechts? <br> | |||
{{LearningApp|app=13484195|width=100%|height=800px}}<br> | |||
|3= Üben}} | |||
{{Box|1=Test:|2= Kennst du den Unterschied zwischen einer natürlichen Zahl, einer ganzen Zahl und einer rationalen Zahl? Hier der Test... <br> | |||
{{LearningApp|app=14486054|width=100%|height=400px}}<br> | |||
|3= Üben}} | |||
{{Box |1= Zum Einstieg: |2= Bearbeite B. S. 188/ 7! Berechne im Kopf! | |||
{{Lösung versteckt |1= '''Lösung B. S. 188/ 7:''' <br> | |||
a) - 1,4; b) - 4,2; c) 1,4; d) 5,9; e) 5,6; f) - 7,1; g) 3,5; h) - 1,4; | |||
|2= Lösung B. S. 188/ 7 anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box |1= Übung: |2= Bearbeite B. S. 189/ 14! | |||
{{Lösung versteckt |1= '''Lösung B. S. 189/ 14:''' <br> | |||
a) + 4 < 23 <br> | |||
b) - 3,5 < - 2,8 <br> | |||
c) 0 > - 44 <br> | |||
d) 0 = 0 <br> | |||
e) 7,4 > - 8,3 <br> | |||
f) 0 > <math> -\frac{1}{30} </math> <br> | |||
|2= Lösung B. S. 189/ 14 anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box |1= Für Schnelle zur Übung: |2= '''Zur Vertiefung:''' Bearbeite B. S. 189/ 19 a) und b) ! | |||
{{Lösung versteckt |1= '''Lösung B. S. 189/ 19:''' <br> | |||
'''a)''' <br> | |||
+ (- a) + x + a = 0 bzw. die folgende Notation - a + x + a = 0 <br> | |||
sowohl a, als auch x stehen jeweils für eine rationale Zahl. Die Zahl "- a" ist die Gegenzahl der Zahl "a". <br> | |||
Damit die Aufgabe eine Lösung hat, muss '''x = 0''' gelten! <br> | |||
'''b)''' <br> | |||
12,5 = <math>12\frac{1}{2} </math> <br> | |||
12,5 + x = - 12,5 --> x = - 25; der zweite Summand muss - 25 sein! | |||
|2= Lösung B. S. 189/ 19 a) und b) anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box|1=Hausaufgabe:|2= Notiere für die angegebene Zahl die nächstgelegene ganze Zahl! <br> | |||
{{LearningApp|app=14485909|width=100%|height=400px}}<br> | |||
|3= Üben}} | |||
{{Box|1=Hausaufgabe:|2= Ordne die Zahlen der Größe nach! Beginne mit der Kleinsten auf der linken Seite! | |||
{{LearningApp|app=14486701|width=100%|height=400px}}<br> | |||
|3= Üben}} | |||
=20.05.2025: in der Schule= | |||
{{Box|1=Info:|2= Notiere dir bitte zuerst '''Potenzen rationaler Zahlen''' als neue Überschrift in dein Heft. Nun geht es auch schon los mit einem nicht ganz neuen Themengebiet, über Potenzen solltest du doch bereits einiges wissen... | |||
|3=Kurzinfo}} | |||
{{Box|1=Zur Wiederholung wichtiger Inhalte von Potenzen: |2= '''Anmerkung: Das am Ende beschriebene Skript mit Übungsaufgaben musst du nicht suchen, so etwas besitzt du nicht ;-) <br> Für dich geht es einfach i Anschluss hier weiter... :-) <br> | |||
{{LearningApp|app=2553215|width=100%|height=400px}} | |||
|3= Üben}} | |||
{{Box|1=Zum Einstieg: |2= '''Heute geht es, wie du bereits weißt, um Potenzen''' <br> Aber zunächst eine Wiederholung deines bereits vorhandenen Wissens... <br> | |||
Überlege nochmal gründlich, welches Vorzeichen das Ergebnis von <math> (- 3)^2 </math> bzw. <math> (-2)^3 </math> haben wird und begründe auch, weshalb dies so ist! <br> | |||
{{LearningApp|app=1684405|width=100%|height=400px}} | |||
|3= Üben}} | |||
{{Box|1= Überlegung: |2= Bearbeite bitte B. S. 197/ 1! Decke bitte, bevor du startest, die Lösung der Aufgabe zu. Danke! <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 197/ 1:''' <br> | |||
Vergleiche deine Lösung bitte mit der im Buch und verbessere diese gegebenenfalls! | |||
<br> | |||
Schau dir nun nochmal genau deine Lösung oder auch gerne die aus dem Buch an und versuche dir einen Zusammenhang zwischen negativem Exponenten und seiner Wirkung auf die Basis herauszuarbeiten! <br> Vergleiche deine Gedanken mit dem folgenden Merksatz! Notiere diesen bitte anschließend in dein Heft! <br> | |||
Im Rahmen des Merksatzes habe ich auch Beispiele notiert, du kannst diese gerne auch selbst erst berechnen und dann deine Lösung mit der von mir vergleichen. So hast du bereits noch einmal das Umrechnen bei Potenzen geübt. | |||
|2= Lösung anzeigen | 3= Lösung verbergen}} | |||
{{Lösung versteckt|1= | |||
'''Merke: <br> | |||
<u>'''Potenzen rationaler Zahlen:'''</u> <br> | |||
Für rationale Zahlen <math> a \neg 0 </math> und natürliche Zahlen n gilt: <math> a^{-n} = \frac{1}{a^n} </math> <br> | |||
Beispiele: | |||
#<math> 2^{-3} = \frac{1}{2^3} = \frac{1}{2\cdot 2 \cdot 2} = \frac{1}{8} </math> <br> | |||
#<math>(\frac{3}{4})^{-2} = \frac{1}{(\frac{3}{4})^2}=\frac{1}{(\frac{3}{4}) \cdot (\frac{3}{4})} = \frac{1}{(\frac {9}{16})} = 1 \div \frac{9}{16} = 1 \cdot \frac{16}{9} = \frac{16}{9} </math> <br> | |||
#<math> (- 0,5)^{-1} = (-\frac{1}{2})^{-1} = \frac{1}{(-\frac{1}{2})^1} = \frac{1}{(-\frac{1}{2})}= 1 \div (-\frac{1}{2}) = 1 \cdot (-\frac{2}{1})= 1 \cdot (-2) = -2 </math> | |||
|2= Merksatz anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box|1=Übung: |2= Bearbeite B. S. 197/ 2! <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 197/ 2:''' <br> | |||
Anmerkung: Um die Lösung der Aufgabe zu berechnen ist es sinnvoller die Angabe aus dem Buch Schritt für Schritt im Kopf zu berechnen. <br> Bei der Lösung habe ich immer zuerst die Potenz notiert und im Anschluss das Endergebnis.<br> | |||
'''a)''' <br> | |||
<math> (-1)^8 = + 1</math>; <br> | |||
NR: <math> 1\cdot 1 \cdot 1 \cdot 1 \cdot 1 \cdot 1 \cdot 1 \cdot 1 = 1 </math> und 8 ist ein gerader Exponent, deswegen ist das Ergebnis positiv <br> | |||
'''b)'''<br> | |||
<math> (-10)^7 = -10000000 </math>; <br> | |||
NR: <math> 10\cdot 10\cdot 10 \cdot 10 \cdot 10 \cdot 10 \cdot 10 = 10000000 </math> und 7 ist ein ungerader Exponent, deswegen ist das Ergebnis negativ <br> | |||
'''c)'''<br> | |||
<math> (\frac{2}{5})^3 = \frac {2\cdot 2\cdot 2}{5 \cdot 5 \cdot 5} = \frac{8}{125} </math> <br> | |||
'''d)''' <br> | |||
<math> (- 0,1)^5 = - 0,00001 </math>;<br> | |||
NR: <math> 1\cdot 1 \cdot 1 \cdot 1 \cdot 1 = 1 </math> und 5 Nachkommastellen liefern das Endergebnis - 0,00001 <br> | |||
'''e)''' <br> | |||
<math>( -0,4)^5 = - 0,01024 </math>; <br> | |||
NR: <math> 4\cdot 4 \cdot 4 \cdot 4 \cdot 4 = 1024 </math> und 5 Nachkommastellen liefern das Endergebnis - 0,01024 <br> | |||
'''f)''' <br> | |||
<math> (-\frac{1}{3})^3 = -\frac{1}{27}</math>; <br> | |||
NR: <math> 1\cdot 1 \cdot 1 = 1 </math> und <math> 3\cdot 3 \cdot 3 = 27 </math> <br> | |||
|2= Lösung B. S. 197/ 2 anzeigen | 3= Lösung verbergen}} <br> | |||
<br> | |||
|3= Üben}} | |||
{{Box|1=Zum Abschluss: |2= Bearbeite B. S. 198/3! <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 198/ 3:''' <br> | |||
Anton hat Recht. <br> | |||
<math> -1,5 ^2</math> bedeutet, nur 1,5 wird mit 2 potenziert, das Minuszeichen nicht! <br> | |||
Vielleicht erinnerst du dich, dass um Zahl und Minuszeichen eine Klammer gesetzt sein muss, damit sich der Exponent auch auf das Minuszeichen bezieht. <br> | |||
Achtung: | |||
*<math> - 1,5^2 = - 1,5 \cdot 1,5 = - 2,25 </math> | |||
*<math> (-1,5)^2= (- 1,5) \cdot (-1,5) = + 2,25 </math> | |||
|2= Lösung B. S. 198/ 3 anzeigen | 3= Lösung verbergen}} <br> | |||
<br> | |||
|3= Üben}} | |||
=20.05.2025: Hausaufgabe= | |||
{{Box|1=Hausaufgabe - wähle mindestens 3 Aufgaben aus, die du als Hausaufgabe bearbeitest! |2= Nun werden die Aufgaben etwas länger, berechne bitte Schritt für Schritt, vergleiche immer dein Ergebnis mit meinem Lösungsvorschlag, bevor du die nächste Aufgabe berechnest! <br> Bearbeite nun bitte folgende Aufgaben: B. S. 196/ 6 g), 7 d), e), f), g), j)! <br> | |||
''Hilfestellung:'' Überlege dir bei jeder Teilaufgabe von B. S. 196/ 7 zunächst, ob das Endergebnis positiv oder negativ sein wird. <br> Schreibe entsprechend das Vorzeichen vor eine große Klammer und berechne das Produkt bzw. den Quotienten, so wie du es von früher bereits gewohnt bist, um die Vorzeichen musst du dir keine Gedanke mehr machen, die hast du ja bereits berücksichtigt. | |||
{{Lösung versteckt |1= '''Lösung B. S. 196/ 6g):''' <br> | |||
<math> -17,25 - 25\frac{1}{3} + 58\frac{3}{4} - 37 \frac{1}{2} + 19\frac{2}{5} - 38,4= </math> <br> | |||
<math> -17,25 - 25\frac{1}{3} + 58,75 - 37,5 + 19,4 - 38,4= </math><br> | |||
<math> 19,4 - 38,4 + (58,75 - 17,25 - 37,5) - 25\frac {1}{3} = </math><br> | |||
<math> - 19 + (41,5 - 37,5) - 25\frac{1}{3} = </math><br> | |||
<math> -19 + 4 - 25\frac{1}{3} = </math><br> | |||
<math> -15 - 25\frac{1}{3} = -40 \frac{1}{3} </math><br> | |||
|2= Lösung B. S. 196/ 6g) anzeigen | 3= Lösung verbergen}} <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 196/ 7d):''' <br> | |||
<math> (-0,6) \div 0,5 \div 1,5 \div 1,6 = </math> <br> | |||
<math> - \frac{3}{5} \div \frac {1}{2} \div \frac{3}{2} \div \frac{16}{10} = </math><br> | |||
<math> - \frac {3}{5} \cdot \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{10}{16} = </math><br> | |||
<math> - \frac {3 \cdot 2 \cdot 2 \cdot 5 \cdot 2 } {5 \cdot 1 \cdot 3 \cdot 2 \cdot 2 \cdot 2 \cdot 2 } = </math><br> | |||
<math>- \frac{1}{2} = </math><br> | |||
<math> - 0,5 </math> | |||
|2= Lösung B. S. 196/ 7d) anzeigen | 3= Lösung verbergen}} <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 196/ 7e):''' <br> | |||
<math> -\frac{1}{2} \div \frac{4}{5} \div (-\frac{5}{3}) \div (-\frac {4}{9}) = </math> <br> | |||
<math> -(\frac{1}{2} \cdot \frac{5}{4} \cdot \frac{3}{5}\cdot \frac {9}{4}) = </math> <br> | |||
<math> -\frac {1 \cdot 5 \cdot 3 \cdot 9 } {2 \cdot 4 \cdot 5 \cdot 4} = </math><br> | |||
<math> - \frac{27}{32} </math> | |||
|2= Lösung B. S. 196/ 7e) anzeigen | 3= Lösung verbergen}} <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 196/ 7f):''' <br> | |||
<math> (-\frac{1}{2}) \cdot \frac{4}{5} \cdot (-\frac{5}{3}) \cdot (-\frac {3}{4}) = </math> <br> | |||
<math> -\frac {1 \cdot 4 \cdot 5 \cdot 3 } {2 \cdot 5 \cdot 3 \cdot 4} = </math><br> | |||
<math>- \frac{1}{2} = </math><br> | |||
<math> - 0,5 </math> | |||
|2= Lösung B. S. 196/ 7f) anzeigen | 3= Lösung verbergen}} <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 196/ 7g):''' <br> | |||
<math> \frac{3}{4} \cdot (-0,5) \cdot (-\frac{4}{5}) \cdot (-\frac {4}{3}) \cdot \frac{5}{6} = </math> <br> | |||
<math> \frac{3}{4} \cdot (- \frac{1}{2} ) \cdot (-\frac{4}{5}) \cdot (-\frac {4}{3}) \cdot \frac{5}{6} = </math> <br> | |||
<math> -\frac {3 \cdot 1 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 5 } {2 \cdot 2 \cdot 2 \cdot 5 \cdot 3 \cdot 2 \cdot 3 } = </math><br> | |||
<math>- \frac{1}{3} = </math><br> | |||
|2= Lösung B. S. 196/ 7g) anzeigen | 3= Lösung verbergen}} <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 196/ 7j):''' <br> | |||
<math> (- 0,25) \div \frac{1}{8} \div (-\frac {1}{2}) \div (-0,4) = </math> <br> | |||
<math> (- \frac{1}{4} ) \div \frac{1}{8} \div (-\frac {1}{2}) \div (-\frac{2}{5}) = </math> <br> | |||
<math> - (\frac{1}{4} \div \frac{1}{8} \div \frac {1}{2} \div \frac{2}{5} ) = </math> <br> | |||
<math> - (\frac{1}{4} \cdot \frac{8}{1} \cdot \frac {2}{1} \cdot \frac{5}{2} ) = </math> <br> | |||
<math> -\frac {1 \cdot 2 \cdot 4 \cdot 2 \cdot 5} {4 \cdot 1 \cdot 1 \cdot 2 } = </math><br> | |||
<math>- \frac{10}{1} = - 10 </math><br> | |||
|2= Lösung B. S. 196/ 7j) anzeigen | 3= Lösung verbergen}} <br> | |||
<br> | |||
|3= Üben}} | |||
=30.05.2025: Aufgaben für die heutige Doppelstunde - nutze die Zeit zum Üben! = | |||
{{Box|1= Zum Start in die heutige Mathematikstunde: |2= Rechne im Kopf! Achte jeweils darauf zuerst die Schreibweise im Kopf zu vereinfachen! <br> | |||
{{LearningApp|app=1118403|width=100%|height=600px}} | |||
|3=Üben}} | |||
{{Box |1= Weiter zum Warmwerden: |2= Bearbeite B. S. 188/ 8 g), l) und B. S. 188/ 9 d), e) l)! <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 188/ 8 g) und l):''' <br> | |||
'''g)''' <br> | |||
<math> - 0,9 + \frac{4}{15} = -\frac{9}{10} + \frac{4}{15}= -\frac{27}{30} + \frac {8}{30} = -\frac{19}{30}; </math> <br> | |||
'''l)''' <br> | |||
<math> (-2\frac{5}{8}) + (-1\frac{3}{4})= -2 \frac{5}{8} -1 \frac{6}{8} = - 3 \frac{11}{8} = -4\frac{3}{8}; </math> <br> | |||
|2= Lösung B. S. 189/ 8 anzeigen | 3= Lösung verbergen}} <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 188/ 9 d), e) und l):''' <br> | |||
'''d)''' <br> | |||
<math> - 8,5 + (-4\frac{1}{2}) = - 8,5 - 4,5 = - 13 </math> <br> | |||
'''e)''' <br> | |||
<math> 12,3 + (-15,4) = 12,3 - 15,4 = - 3,1 </math> <br> | |||
'''l)''' <br> | |||
<math> 0 + (-24,6) + 26,4 = 0 - 24,6 + 26,4 = - 24,6 + 26,4 = 1,8 </math> | |||
|2= Lösung B. S. 189/ 9 anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box|1= Zur Wiederholung:|2= Wie du weißt, benötigt man zum vorteilhaften Rechnen die Rechengesetze, d.h. zunächst vor allem das Kommutativgesetz ("a + b = b + a" und "a <math> \cdot </math> b = b <math> \cdot </math> a") und auch das Assoziativgesetz ("a + b + c = (a + b) + c = a + (b + c)" und "<math> a \cdot b \cdot c = (a \cdot b) \cdot c = a \cdot ( b \cdot c) </math>"). <br> Mit folgender App kannst du dein Wissen zu Kommutativ-, Assoziativ- und auch Distributivgesetz wiederholen: <br> {{LearningApp|app=1688133|width=100%|height=600px}} | |||
|3=Üben}} | |||
{{Box |1= Übung: |2= Bearbeite B. S. 189/ 12 c) und f)! <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 189/ 12 c) und f):''' <br> | |||
'''c)''' <br> | |||
3,12 - 3,38 - 4,52 + 2,78 = 3,12 + 2,78 + (- 3,38 - 4,52) = 5,9 + (- 7,9) = 5,9 - 7,9 = -2 <br> | |||
ODER:<br> | |||
3,12 - 3,38 - 4,52 + 2,78 = 3,12 - 4,52 + (2,78 - 3,38) = - 1,4 + (- 0,6) = - 1,4 - 0,6 = - 2 <br> | |||
'''f)''' <br> | |||
<math> -\frac{1}{2} + \frac{3}{5} + \frac{1}{4} + \frac{6}{15} - \frac{3}{8} = \frac{3}{5} + \frac{6}{15} + (\frac{2}{8} - \frac{3}{8} - \frac{4}{8}) = \frac{9}{15} + \frac{6}{15} + (- \frac{1}{8} - \frac{4}{8}) = \frac{15}{15} + (- \frac{5}{8}) = 1 - \frac{5}{8} = \frac{8}{8} - \frac{5}{8} = \frac{3}{8} </math> | |||
|2= Lösung B. S. 189/ 12 anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box |1= Übung: |2= Bearbeite B. S. 192/ 8! Denke hier an die Verwendung der Rechengesetze!<br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 192/ 8:''' <br> | |||
'''a)''' <br> | |||
<math> 0,7 \cdot (-20)\cdot (- 0,3) \cdot (- 5) = 0,7 \cdot (-0,3) \cdot ((- 20) \cdot (- 5)) = - 0,21 \cdot 100 = - 21 </math> <br> | |||
'''b)''' <br> | |||
<math> 1,2 \cdot (-25) \cdot (- 1,5) \cdot (- 40) = - 25 \cdot (- 40) \cdot (1,2 \cdot (- 1,5)) = 1000 \cdot (- 1,80) = - 1800 </math> <br> | |||
'''c)''' <br> | |||
<math> 4 \cdot (- 7) \cdot \frac{1}{14} \cdot (- 1) = 4 \cdot ( (-7) \cdot (-1) \cdot \frac{1}{14}) = 4 \cdot (7 \cdot \frac{1}{14})=4 \cdot \frac{1}{2} = 2 </math> | |||
|2= Lösung B. S. 192/ 8 anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box|1=Übung: |2= Bearbeite B. S. 196/ 8 a), b), c)! Beachte bitte, du sollst hier nicht rechnen, sondern nur entscheiden, ob das Ergebnis positiv oder negativ ist. Bitte nicht raten, sondern Schritt für Schritt jede Aufgabe betrachten und entscheiden. <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 196/ 8 a), b), c):''' <br> | |||
'''a)''' <br> | |||
Klammern aufgelöst: <math> - 241 \frac {3}{5} - 197 \frac{4}{7} - 88 \frac{5}{11} - 16\frac{4}{9} </math> <br> | |||
Erkenntnis: Man startet bei einer negativen Zahl und "läuft immer weiter weg" von der Null und zwar auf der Zahlengeraden weiter nach links und bleibt somit im negativen Bereich. <br> | |||
Das Ergebnis ist also '''negativ'''. | |||
'''b)''' <br> | |||
Klammern aufgelöst: <math> 154 \frac {2}{7} + 311 \frac{5}{8} + 220 \frac{1}{5} + 57\frac{3}{4} </math> <br> | |||
Erkenntnis: Man startet bei einer positiven Zahl und "läuft" auf der Zahlengeraden weiter nach rechts und bleibt somit im positiven Bereich. <br> | |||
Das Ergebnis ist also '''positiv'''. | |||
'''c)''' <br> | |||
Klammern aufgelöst: <math> 58 \frac {1}{2} + 0,745 - 68 \frac{3}{4} + 0,052 </math> <br> | |||
<math> 58 \frac {1}{2} - 68 \frac{3}{4} < 0 </math> und zwar kleiner als - 10, d.h. der Aufgabenteil <math> + 0,745 + 0,052 </math>, welcher größer 0, aber kleiner 1 ist, führt nicht dazu, dass das Ergebnis der Aufgabe positiv wird und deswegen ist das Endergebnisergebnis dieser Aufgabe '''negativ'''. | |||
|2= Lösung anzeigen | 3= Lösung verbergen}} <br> | |||
<br> | |||
|3= Üben}} | |||
{{Box|1=Übung: |2= Bearbeite B. S. 200/ 4! <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 200/ 4:''' <br> | |||
a) <br> | |||
Carolin hat hier Punkt vor Strich missachtet.<br> | |||
<math>2,5 - 12,5 \div 0,4 = 2,5 - 125 \div 4 = 2,5 - 31,25 = - 28,75 </math> <br> | |||
b) <br> | |||
Hätte Carolin "von links nach rechts" beachtet, wäre ihr dieser Fehler nicht passiert!<br> | |||
Vor der 2 steht nämlich ein Minuszeichen und vor <math> \frac{1}{6} </math> steht ein Pluszeichen. Wenn Carolin die gerne zuerst rechnen möchte, muss sie das Minuszeichen vor der 2 beachten, das Ergebnis von <math> - 2 + \frac{1}{6} </math> wäre <math> -1\frac{5}{6} </math>. <br> | |||
Nun aber von links nach rechts gerechnet: <br> | |||
<math>- \frac{1}{3} - 2 + \frac{1}{6} = -2\frac{1}{3} + \frac{1}{6} = - 2 \frac{2}{6} + \frac{1}{6} = - 2 \frac {1}{6}</math> <br> | |||
c)<br> | |||
Carolin hat Potenz vor Punkt missachtet! <br> | |||
<math>1- 1,2 \cdot 0,5^2 = 1- 1,2 \cdot 0,25 = 1- 0,3 = 0,7 </math> <br> | |||
NR.: <math> 12 \cdot 25 = 300 </math> und 1,2 und 0,25 haben gemeinsam 3 Nachkommastellen, daher ist das Ergebnis des Produktes <math> 1,2 \cdot 0,25 = 0,300 = 0,3 </math>. | |||
|2= Lösung B. S. 200/ 4 anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box| Zur Erinnerung an das Gliedern von Termen - bitte berechne die Aufgabe im Video selbst, d.h. klicke zunächst auf Pause, wenn das Blatt im Video nach oben geschoben wird, berechne die Aufgabe und klicke anschließend wieder auf Play, um deine Lösung mit der Lösung im Video Schritt für Schritt zu vergleichen. Verbessere in Rot! |{{#ev:youtube|zWbpQrVYYK4}} | Hervorhebung1}} <br> | |||
{{Box|1=Zur Wiederholung der Termart: |2= Erinnerung: Die letzte auszuführende Rechnung bestimmt die Art des Terms. <br> Klicke bei der folgenden App immer zunächst "Summe", "Differenz", "Produkt" oder "Quotient" an und wähle anschließend den Term entsprechend der angeklickten Termart aus. <br> Bitte nicht raten, sondern überlege dir bei jeder einzelnen Aufgabe, wie du diese berechnen würdest und entscheide dann aufgrund der letzten Rechnung, um welche Termart es sich bei den Termen jeweils handelt. <br>{{LearningApp|app=3055847|width=100%|height=800px}}<br> | |||
|3= Üben}} | |||
{{Box|1=Zur Wiederholung: Notiere jeden Term zunächst in Wortform in dein Heft und berechne seinen Wert Schritt für Schritt ins Heft! Ordne anschließend den Term in Wortform, berechnete Zwischenschritte und den Termwert dem passenden Term zu! |2= {{LearningApp|app=pbrc4n4ea21|width=100%|height=800px}}<br> | |||
|3= Üben}} | |||
{{Box|1=Zur Wiederholung: |2= {{LearningApp|app=18211707|width=100%|height=800px}}<br> | |||
|3= Üben}} | |||
{{Box| FREIWILLIG FALLS DU NOCH HILFE BRAUCHST: Zusammenfassung und Wiederholung - hier kannst du dir nochmal, falls du das möchtest, ganz genau Schritt für Schritt erklären lassen, wie man rationale Zahlen addiert, subtrahiert, multipliziert und dividiert. Am Besten du rechnest die Aufgaben während des Videos im Kopf mit. |{{#ev:youtube|Qh1EWvJxFlA}} |Hervorhebung1}} <br> | |||
=18.07.2025: Aufgaben für die heutige Doppelstunde - nutze die Zeit zum Üben und Vertiefen! = | |||
{{Box |1= Zunächst ein paar Aufgaben zur Prozentrechnung, damit du hier dein Wissen rund ums Prozentrechnen testen und weiter vertiefen kannst! |2= Bearbeite B. S. 246/ 1; 2; 3 und 4! <br> Hinweis: Für die Berechnung der Lösungen von Aufgabe 1 ist es ausnahmsweise erlaubt den Taschenrechner des Tablets zu verwenden, sonst kommt ihr nicht zur Berechnung weiterer Aufgaben... Falls ihr bei den Aufgaben zur Prozentrechnung nach 20 Minuten verzweifelt sein solltet, fangt bitte mit Aufgaben zum Volumen an. | |||
{{Lösung versteckt |1= '''Lösung der Aufgaben: B. S. 252!'''<br> Korrigiere deine Lösung mit Hilfe der Lösung im Buch. Hake richtige Lösungen ab, verbessere falsche Lösungen und falls du noch eine Frage haben solltest, frag bitte unbedingt am kommenden Montag im Unterricht! ''' <br> | |||
|2= Lösung anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box |1= Wichitg: |2= Bearbeite die folgenden Aufgaben entweder der Reihe nach oder wähle sie entsprechend danach aus, was du im Rahmen des Volumens noch vertiefen möchtest... | |||
|3= Üben}} | |||
{{Box|1=Übung:|2= Es ist sehr wichtig zur Bearbeitung verschiedener Aufgabenstellungen den Unterschied zwischen Fläche und Volumen zu kennen. Ob du dies bereits eindeutig unterscheiden kannst, erfährst du durch folgende Aufgabe! <br>{{LearningApp|app=6767707|width=100%|height=400px}}<br> | |||
|3= Üben}} | |||
{{Box|1=Übung:|2= Suche passende Paare, indem du jeweils die Volumeneinheiten entsprechend umrechnest! <br> {{LearningApp|app=p1argwri221|width=100%|height=600px}} | |||
|3= Üben}} | |||
{{Box |1= Übung: |2= Wichtig: Lies ganz genau, welche Teilaufgaben nun zu bearbeiten sind! B. S. 161/ 9 b); d); B. S. 161/ 10 c); d); B. S. 161/ 11 a); Verbessere deine Lösungen jeweils Schritt für Schritt mit der von mir, streiche ggf. falsche Lösungen durch und notiere in Rot die richtige Lösung! <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 161/ 9 b) und d):''' <br> | |||
'''b)''' <br> | |||
18280 cm³ <br> 41050 cm³ <br> 4005 cm³ <br> 20010 cm³ <br> | |||
'''d)''' <br> | |||
19030 ml <br> 9004 ml <br> 10250 ml <br> | |||
|2= Lösung B. S. 161/ 9 b) und d) anzeigen | 3= Lösung verbergen}} <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 161/ 10 c) und d):''' <br> | |||
'''c)''' <br> | |||
2 m³ 550 dm³ <br> 43 m³ 700 dm³ <br> 42 dm³ 43 cm³ <br> 8 l 70 ml <br> | |||
'''d)''' <br> | |||
18 l 400 ml <br> 9 l 200 ml <br> 0 m³ 75 dm³ <br> 5 dm³ 98 cm³ <br> | |||
|2= Lösung B. S. 161/ 10 c) und d) anzeigen | 3= Lösung verbergen}} <br> | |||
{{Lösung versteckt |1= '''Lösung B. S. 161/ 11 a) und d):''' <br> | |||
'''a)''' <br> | |||
4,725 m³ <br> 3,4 dm³ <br> 4,05 dm³ | |||
'''d)''' <br> | |||
0,8 m³ <br> 0,05 dm³ <br> | |||
|2= Lösung B. S. 161/ 11 a) und d) anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box|1=Test:|2= Zur Vertiefung: <br> {{LearningApp|app=pa840vzxj21|width=100%|height=600px}} | |||
|3= Üben}} | |||
{{Box|1=Zur Vertiefung:|2= Hier kannst du nochmal testen, ob du die Volumeneinheiten bereits gut umrechnen kannst! <br>{{LearningApp|app=11129145|width=100%|height=800px}}<br> | |||
{{LearningApp|app=1924298|width=100%|height=400px}} <br> | |||
|3= Üben}} | |||
{{Box |1= Übung: |2= Bearbeite B.S. 164/ 5 b) und d)! | |||
{{Lösung versteckt |1= '''Lösung B. S. 164/ 5 b) und d):''' <br> | |||
'''Rechne zunächst in eine gemeinsame Einheit um!''' | |||
'''a)''' <br> | |||
<math> V = a \cdot b \cdot c = 44 mm \cdot 1,2 dm \cdot 8 dm = 44 mm \cdot 120 mm \cdot 800 mm = 5280 mm^2 \cdot 120 mm = 4224000 mm^3 = 4224 cm^3 </math> | |||
'''c)''' <br> | |||
<math> V = a \cdot b \cdot c = 15 cm \cdot 1,5 cm \cdot 1,2 dm = 15 cm \cdot 1,5 cm \cdot 12 cm = 22,5 cm^2 \cdot 12 cm = 270 cm^3 </math> | |||
|2= Lösung B. S. 164/ 5 b) und d) anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box|1=Zur Vertiefung und Wiederholung: Achtung beim Rechnen mit Einheiten - hier konkret bei der Division!|2= Hier kannst du testen, ob du dies bereits gut verstanden hast...Achte dabei genau auf die jeweiligen Einheiten! <br>{{LearningApp|app=pz3do6e9j21|width=100%|height=800px}}<br> | |||
|3= Üben}} | |||
{{Box| Zur Erinnerung: |FREIWILLIG: Wenn du magst, kannst du dir die folgende Information in dein Heft notieren. <br> | |||
{{Lösung versteckt|1= | |||
'''Merke: <br> | |||
<u>'''Strategien zum Berechnen des Volumens zusammengesetzter Körper'''</u> <br> | |||
1. ''Strategie: Zerlegen'' <br> | |||
Man zerlegt den Körper in geeignete Teilkörper und berechnet die Volumina der einzelnen Teilkörper. <br> Das Volumen des gesuchten Körpers erhält man durch Addition der Volumina aller Teilkörper. <br> | |||
2. ''Strategie: Ergänzen'' <br> | |||
Man ergänzt den Körper geeignet, berechnet das Volumen des so neu entstandenen Körpers. Anschließend subtrahiert man vom Volumen des neu entstandenen Körpers das Volumen des ergänzten Körpers. So erhält man das Volumen des gesuchten Körpers. | |||
|2= Information aufdecken |3= Verbergen}} | |||
|3=Merksatz}} | |||
{{Box |1= Übung: |2= Bearbeite nun B. S. 170/ 3 b)! Entscheide dich bei der Lösung der Aufgabe für eine der beiden Strategien! Vergleiche deine Lösung mit meiner und überlege, indem du dir beide Lösungsvarianten genau anschaust, welche Strategie hier schneller ans Ziel führt! | |||
{{Lösung versteckt |1= '''Lösung B. S. 170/ 3 b) :''' <br> | |||
'''1. Möglichkeit - Strategie Zerlegen:''' <br> | |||
<math>V = 2 \cdot (11 cm \cdot 17 cm \cdot 42 cm) + (34 cm - 11 cm - 11 cm) \cdot (17 cm - 7 cm) \cdot 42 cm = 2 \cdot (187 cm^2 \cdot 42 cm) + 12 cm \cdot 42 cm \cdot 10 cm = 2 \cdot 7854 cm^3 + 504 cm^2 \cdot 10 cm = 15708 cm^3 + 5040 cm^3 = 20748 cm^3</math> | |||
'''2. Möglichkeit - Strategie Ergänzen:''' <br> | |||
<math>V = 34 cm \cdot 42 cm \cdot 17 cm - 12 cm \cdot 7 cm \cdot 42 cm = 1428 cm^2 \cdot 17 cm - 84 cm^2 \cdot 42 cm = 24276 cm^3 - 3528 cm^3 = 20748 cm^3</math> | |||
<br> | |||
'''Anmerkung:''' <br> | |||
Hier erkennt man sehr schön, dass die Strategie Ergänzen schneller ans Ziel führt. man kann sich also vor Bearbeitung der Aufgabe klug für eine Strategie entscheiden und spart auf diese Weise Zeit und vermutlich auch Nerven... <br> | |||
'''Achtung:''' <math> cm \cdot cm = cm^2 </math> und <math> cm^2 \cdot cm = cm^3 </math> | |||
|2= Lösung B. S. 170/ 3 b) anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box |1= Abschluss "rund ums Volumen": |2= Bearbeite B. S. 178/ 6 b) und c), B. S. 178/ 7 a) (3), (4), (7), (8), 7 b) (1), (2), (3), (4) und B. S. 178/ 10! | |||
{{Lösung versteckt |1= '''Lösung der Aufgaben: B. S. 250!'''<br> Korrigiere deine Lösung mit Hilfe der Lösung im Buch. Hake richtige Lösungen ab, verbessere falsche Lösungen und falls du noch eine Frage haben solltest, frag bitte unbedingt am kommenden Montag im Unterricht! ''' <br> | |||
|2= Lösung anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
Aktuelle Version vom 14. Juli 2025, 16:49 Uhr
31.01.2025: Übungen zu Multiplizieren mit Stufenzahlen und Dividieren durch Stufenzahlen
Zur Vorbereitung zu Hause auf die kommende Stunde - Multiplizieren von Dezimalbrüchen
03.02.25: Weiter geht es mit dem Multiplizieren von Dezimalbrüchen
14.02.2025: Dividieren von Dezimalbrüchen und Hausaufgabe zum Multiplizieren von Dezimalbrüchen
18.02.2025: Hausaufgabe
10.03.2025: Hausaufgabe - Zur Wiederholung
25.03.2025: Hausaufgabe zu Parallelogramm und Wiederholung zu Einheiten
28.03.2025: Hausaufgabe
13.05.2025: Übungen zu rationalen Zahlen
20.05.2025: in der Schule
20.05.2025: Hausaufgabe
30.05.2025: Aufgaben für die heutige Doppelstunde - nutze die Zeit zum Üben!
18.07.2025: Aufgaben für die heutige Doppelstunde - nutze die Zeit zum Üben und Vertiefen!