Dreiecke im Kreis: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (12 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<[[Mathematik 7/7Kongruenz|7 Kongruenz und Dreiecke]] | |||
{{Box|Info|Mit den folgenden Aufträgen kannst du eine besondere geometrische Konstellation erforschen. Beginne mit den Teilen A, B, C und D. Der Teil E ist freiwillig. Notiere deine Aufzeichnungen im Heft und lasse Platz für eine Überschrift|Kurzinfo | {{Box|Info|Mit den folgenden Aufträgen kannst du eine besondere geometrische Konstellation erforschen. Beginne mit den Teilen A, B, C und D. Der Teil E ist freiwillig. Notiere deine Aufzeichnungen im Heft und lasse Platz für eine Überschrift|Kurzinfo | ||
}} | }} | ||
| Zeile 4: | Zeile 5: | ||
{{Box|A - Forscherfeld erkunden|Zeichne in dein Heft einen Kreis. Zeichne dazu ein Dreieck, bei dem alle Eckpunkte auf der Kreislinie liegen und eine Seite Kreisdurchmesser ist. | {{Box|A - Forscherfeld erkunden|Zeichne in dein Heft einen Kreis. Zeichne dazu ein Dreieck, bei dem alle Eckpunkte auf der Kreislinie liegen und eine Seite Kreisdurchmesser ist. | ||
# Untersuche dein Dreieck und schreibe deine Beobachtungen auf. | # Untersuche dein Dreieck und schreibe deine Beobachtungen auf. | ||
# Zeichne weitere Kreise und zugehörige Dreiecke wie in Aufgabe 1. Untersuche alle diese Dreiecke und notiere deine Beobachtungen in deinem Heft. Formuliere eine möglichst allgemeine Aussage als Vermutung.}} | # Zeichne weitere Kreise und zugehörige Dreiecke wie in Aufgabe 1. Untersuche alle diese Dreiecke und notiere deine Beobachtungen in deinem Heft. Formuliere eine möglichst allgemeine Aussage als Vermutung.|Arbeitsmethode}} | ||
{{Lösung versteckt|Betrachte die Winkel der verschiedenen Dreiecke, was fällt dir auf? | |||
|Tipp|Tipp verbergen}} | |||
{{Box|B - Vermutungen begründen| Zerlege die von dir gezeichneten Dreiecke in zwei Teile, indem du den Kreismittelpunkt jeweils mit einem Eckpunkt verbindest. | {{Lösung versteckt|Wenn die Ecken eines Dreiecks so auf einem Kreis liegen, dass eine Seite Kreisdurchmesser ist, dann ist das Dreieck rechtwinklig. | ||
|Lösung|Lösung}} | |||
{{Box|B - Vermutungen begründen|Zerlege die von dir gezeichneten Dreiecke in zwei Teile, indem du den Kreismittelpunkt jeweils mit einem Eckpunkt verbindest. | |||
# Untersuche die entstehenden Teildreiecke. Von welcher besonderen Art sind sie? Schreibe deine Ergebnisse auf und versuche, sie zu begründen. | # Untersuche die entstehenden Teildreiecke. Von welcher besonderen Art sind sie? Schreibe deine Ergebnisse auf und versuche, sie zu begründen. | ||
# Betrachte die Innenwinkel der gezeichneten Dreiecke. Kannst du damit deine Vermutungen aus Teil A begründen? | # Betrachte die Innenwinkel der gezeichneten Dreiecke. Kannst du damit deine Vermutungen aus Teil A begründen? | ||
| | |Arbeitsmethode}} | ||
{{Lösung versteckt|Betrachte die Seiten der verschiedenen Dreiecke, was fällt dir auf? | |||
|Tipp zu 1.|Tipp zu 1. verbergen}} | |||
{{Lösung versteckt|Überlege, wie sich der Winkel γ im großen Dreieck mit Winkel aus dem kleinen Dreieck zusammen setzen lässt. | |||
|Tipp zu 2.|Tipp zu 2. verbergen}} | |||
{{Box|C - Die Aussage umdrehen| | {{Box|C - Die Aussage umdrehen| | ||
# Formuliere eine Umkehrung deiner Ergebnisse aus Teil A, also eine Aussage der Form: „Wenn ein Dreieck ... ist, dann ...“ | # Formuliere eine Umkehrung deiner Ergebnisse aus Teil A, also eine Aussage der Form: „Wenn ein Dreieck ... ist, dann ...“ | ||
# Untersuche an Beispielen, ob diese Umkehrung im Allgemeinen richtig ist. | # Untersuche an Beispielen, ob diese Umkehrung im Allgemeinen richtig ist. | ||
# Versuche, die Umkehrung ggf. zu begründen.| | # Versuche, die Umkehrung ggf. zu begründen.|Arbeitsmethode}} | ||
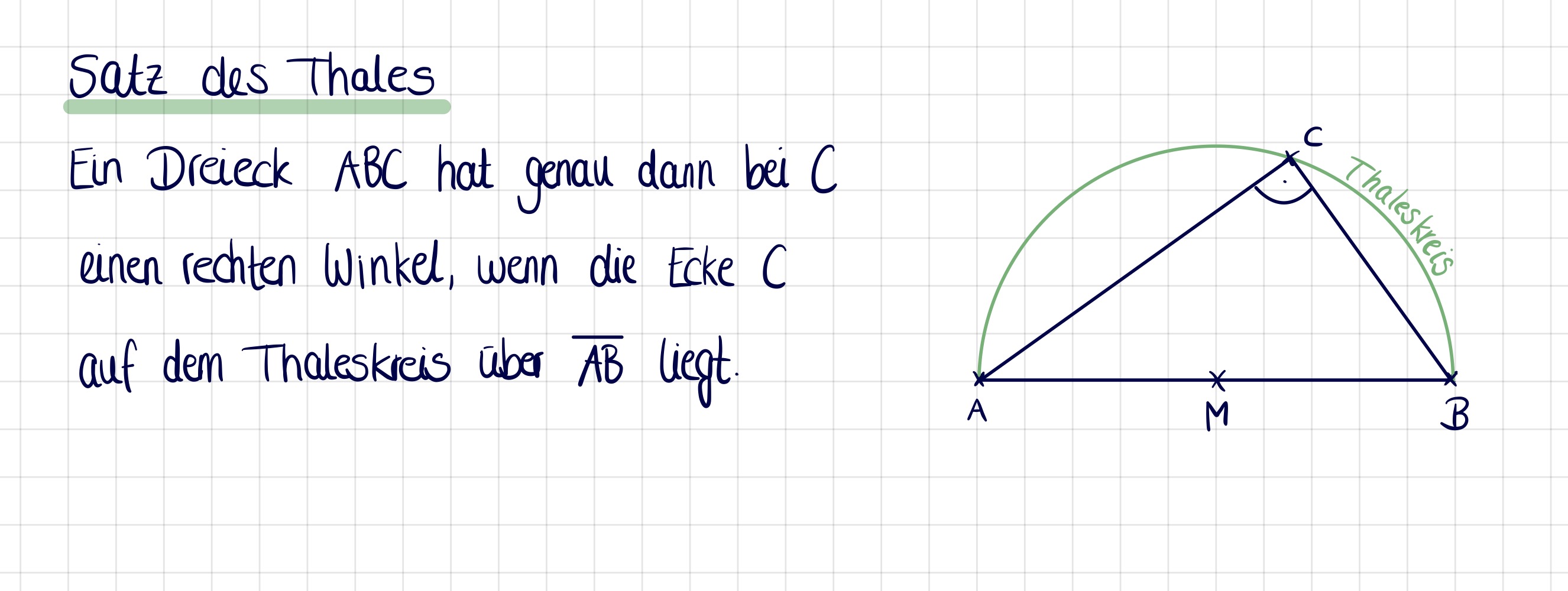
{{Box|D - Ergebnisse notieren|Du bist bei deinen Forschungen auf den sogenannten „Satz des Thales“ gestoßen. Ergänze die Überschrift ''4 Satz des Thales'' über deinen Notizen und notiere dir dann folgenden Merksatz:| | {{Box|D - Ergebnisse notieren|Du bist bei deinen Forschungen auf den sogenannten „Satz des Thales“ gestoßen. Ergänze die Überschrift ''4 Satz des Thales'' über deinen Notizen und notiere dir dann folgenden Merksatz mit Skizze|Arbeitsmethode}} | ||
}} | |||
{{Lösung versteckt|[[Datei:Satz des Thales Hefteintrag.jpg|medium]]|Merksatz|Merksatz|Merksatz verbergen}} | |||
{{Box|E - Im Internet recherchieren||Arbeitsmethode}} | |||
{{ | {{Lösung versteckt|Du bist bei deinen Forschungen auf den sogenannten „Satz des Thales“ gestoßen. Informiere dich im Internet über Thales von Milet und den Satz des Thales. | ||
}} | |Rechercheauftrag|Rechercheauftrag verbergen}} | ||
Aktuelle Version vom 16. April 2024, 10:23 Uhr
Betrachte die Winkel der verschiedenen Dreiecke, was fällt dir auf?
Wenn die Ecken eines Dreiecks so auf einem Kreis liegen, dass eine Seite Kreisdurchmesser ist, dann ist das Dreieck rechtwinklig.
Betrachte die Seiten der verschiedenen Dreiecke, was fällt dir auf?
Überlege, wie sich der Winkel γ im großen Dreieck mit Winkel aus dem kleinen Dreieck zusammen setzen lässt.
Du bist bei deinen Forschungen auf den sogenannten „Satz des Thales“ gestoßen. Informiere dich im Internet über Thales von Milet und den Satz des Thales.