Mathe 7B 2122

<7b 2021 22 

7.2 Kongruenzsätze in Dreiecken

Suche auf folgender Seite deinen Auftrag. M7 7.2 Kongruenzsätze für Dreiecke

Arbeitsauftrag vom Do 30.06.22

Heute geht es um den Satz des Thales:
M7 7.5 Satz des Thales

Arbeitsauftrag vom Fr 18.03.22

• 1. Klebe die Information zu der Winkelhalbierenden ins Merkheft.
• 2. Zeichne die Konstruktion von der rechten Tafel ab und führe die Konstruktionsschritte aus.
• 3. Hole das AB vorne links am Fenster zu den Grundkonstruktionen. Bearbeite die Aufgaben und vergleiche danach mit der Lösung.
• 4 Lese folgenden Text und bearbeite das Quiz.

Winkel

Info

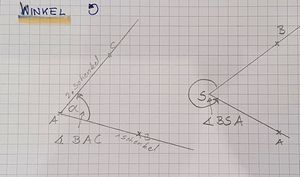
Dreht man einen Schenkel/eine Halbgerade um ihren Anfangspunkt A, so entsteht ein Winkel. Man kann sie mit griechischen Buchstaben wie $\alpha, \beta$ bezeichnen.

Oft hat man z.B. in einem Dreieck auch 3 Punkte A, B und C.

Der Winkel $\alpha$ wird auch häufig so geschrieben: $\sphericalangle BAC$ (siehe rechts) Dabei ist der Winkel bei A gemeint. B liegt dann auf dem einen und C auf dem anderen Schenkel. Die Punkte/Schenkel werden immer gegen den Uhrzeigersinn genannt. Tauscht man die Buchstaben und damit die Punkte, wird ein anderer Winkel angegeben. (siehe rechtes Bild mit dem überstumpfen Winkel).

Bearbeite nun folgendes Quiz:

Der Winkel $\beta$ wird auch häufig so geschrieben: $\sphericalangle CBA$ Dabei ist der Winkel bei B gemeint.

Der Winkel $\gamma$ wird auch häufig so geschrieben: $\sphericalangle ACB$ Dabei ist der Winkel bei C gemeint.

Die Winkel $\sphericalangle BCA$ und $\sphericalangle ABC$ liegen außerhalb des Dreiecks ABC.

• 5. Bearbeite S.72/4c in dem gestern gezeichneten Dreieck. (Lösung liegt vorne aus. Vergleiche sofort.)
• 6. Konstruiere einen Winkel der Größe 45°. Zeichne zuerst eine Gerade.

Ein 45° Winkel ist halb so groß wie ein rechter Winkel (90°). Zeichne erstmal einen rechten Winkel.

• 7. Nimm die Schatzkarte und den dazugehörigen Arbeitsauftrag rechts neben der Tafel.
• 8. Zeige mir deine Schatzkarte.
• 9. Nun darfst du mit Geogebra arbeiten: S.75/19,20

Der Mittelpunkt des Kreises hat zu R und S den gleichen Abstand. Überlege, welche Grundkonstruktion diese Eigenschaft besitzt.

Überlege, welche Grundkonstruktion benutzt werden muss. Du kannst auch einfach alle drei ausprobieren und dann die Punkt D und E an dieser Geraden spiegeln und schauen, was passiert.

• 10. Bearbeite nun S.73/16
• 11. Die letzten Übungen für heute: S.76/27, 28

Alle Punkte, die von A und B gleich weit entfert sind. Überlege, welche Grundkonstruktion diese Eigenschaft besitzt.

Alle Punkte, die von einer Geraden CD den gleichen Abstand haben. Welche Gerade hat diese Eigenschaft? Die Geraden dürfen sich nicht treffen.

Es gibt 2 Parallelen, die man mit zwei Loten (wie gestern im Unterricht erwähnt) konstruieren kann.

Schau mal vorne auf meine Lösung.

Überlege, welche Grundkonstruktion benutzt werden muss. Du kannst auch einfach alle drei ausprobieren und dann die Punkt D und E an dieser Geraden spiegeln und schauen, was passiert.

• 12. Schneller fertig. Dann macht doch das Quiz zur Geometrie.

Kreis	Das zeichne ich, wenn ich alle Punkte um A haben möchte, die den Abstand 2cm haben.
Lot	Ich brauche die kürzeste Strecke zwischen einem Punkt und einer Geraden.
Winkelhalbierende	Alle Punkte auf dieser Geraden haben zu den Schenkeln den gleichen Abstand.
Mittelsenkrechte	Alle Punkte, die zu den Punkten A und B den gleichen Abstand haben, liegen auf ihr.

Arbeitsauftrag vom Fr 3.12.21

Nun hast du das Arbeitsblatt bis Aufgabe 4 bearbeitet.

Bearbeite folgende 3 Learningapps:

Weil du so gut gearbeitet hast, hier ein paar Knobelaufgaben für dich, bis es ans Kahoot geht. Wir beginnen um 9:10.

Rätsel der Woche:

Löse folgendes Rätsel. Die Lösung des Rätsels erhältst du nächste Woche.

Streichhölzer

Du darfst dich bei Mathe-im-Advent.de einloggen, wenn du möchtest oder du bearbeitest die ersten beiden Tage. Aufgaben liegen vorne aus.

HAUSAUFGABE:

1. Du hast 2 Zettel bekommen mit 4 Vierecken darauf. Notiere zu jedem der 4 Vierecke je einen anderen Terme zur Berechnung des Flächeninhalts. Markiere dabei auf jedem Viereck und in deinem Term deine Idee mit Hilfe von Farben. Notiere auch die Formeln der Flächeninhalte in die jeweiligen Flächen.

1. AB fertig

Arbeitsauftrag vom Fr 29.10.21

Hier geht es lang! -->

Arbeitsauftrag vom Do 28.10.21

1. Lies den Merkhefteintrag nochmal durch und lasse das Merkheft offen neben dir liegen.

2. Sortiere gleichartige Produkte.

a²b	$-0,5 a^2 b$	$5 a^2 b$	$b \cdot a^2 \cdot 3$
2ab²	$-2b\cdot a\cdot b$	$b\cdot b\cdot 4a$
a²b²	$a\cdot a\cdot b \cdot b$	$4a^3 :a \cdot b \cdot b$	$a\cdot \frac{1}{2} a\cdot b^2$

3. Bearbeite S.40/2a-c,f (wie im Beispiel im Merkheft)

4. Lies im Buch S.40 oben den Kasten zu Klammern.

5. Notiere den Kasten in dein Merkheft. Markiere in rot das Minus vor der Klammer und das somit veränderte Rechenzeichen wie folgt:

       a - (b + c) = a - b - c 

6. Notiere die Beispiele rechts am Kasten.

7. Noch ein Spiel. Setze das richtige Rechenzeichen und vereinfach so weit wie möglich:

Das '+' als Vorzeichen müsst ihr weglassen.
a - ( a + 2b) = a -() a -()2b = -2b()
a - ( a - 2b) = a -() a +()2b =2b()

Jetzt wird es etwas schwerer.
a - ( -a + 2b - 2c) = a +() a -()2b +()2c
- ( a - 4c²) = -() a +() 4c²

5x -(4y + 2x)-(8x-y)
= 5x -()4y -() 2x-()8x+()y
= -5()x -3()y

8. Notiere das Beispiel S.41/2a in dein Merkheft. Markiere wieder die sich ändernden Vorzeichen.

9. Bearbeite S.41/6a-d, 10 (ohne c)

10. Der Rest ist Hausaufgabe. Denk auch an die Hausaufgabe von gestern S.37/11a,c