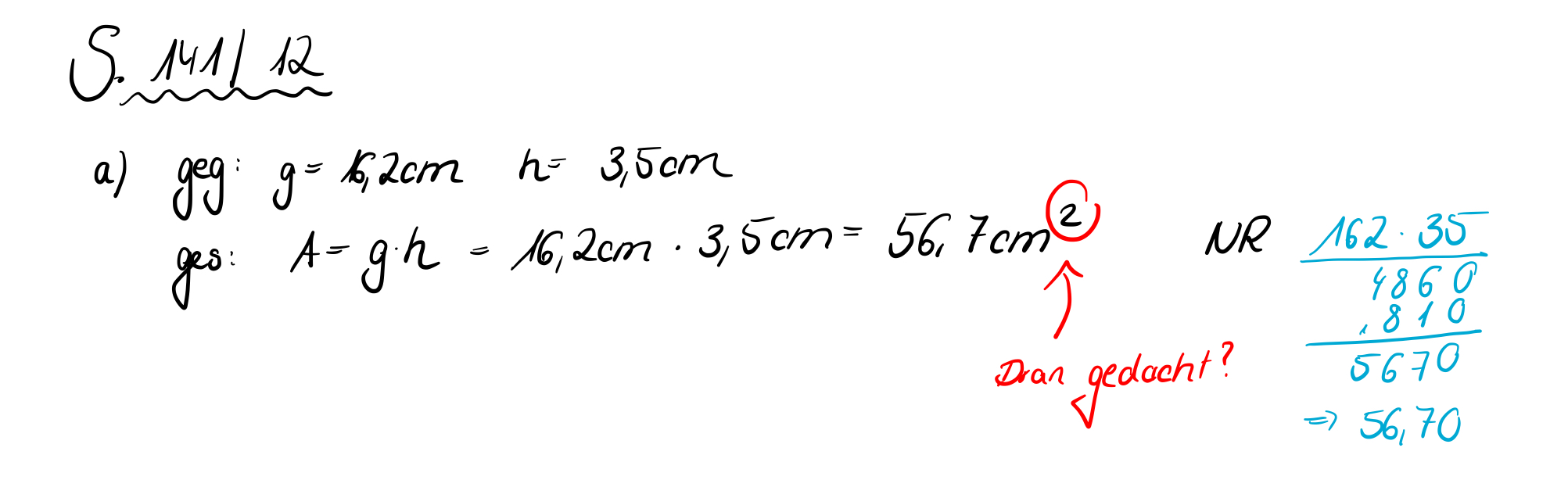M6 4.1 Flächeninhalt eines Parallelogramms: Unterschied zwischen den Versionen
Aus RMG-Wiki
Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (27 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
===Höhe im Parallelogramm=== | ===Höhe im Parallelogramm=== | ||
Notiere in dein Merkheft:<br> | Notiere in dein Merkheft:<br> | ||
{{Box-spezial | |||
'''4 Flächeninhalt und Volumen''' | |Titel= '''<u>4 Flächeninhalt und Volumen</u>''' | ||
''' 4.1 Flächeninhalt eines Parallelogramms''' | |Inhalt= | ||
{{Box-spezial | |||
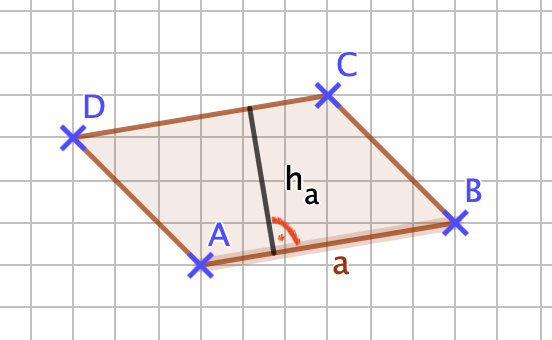
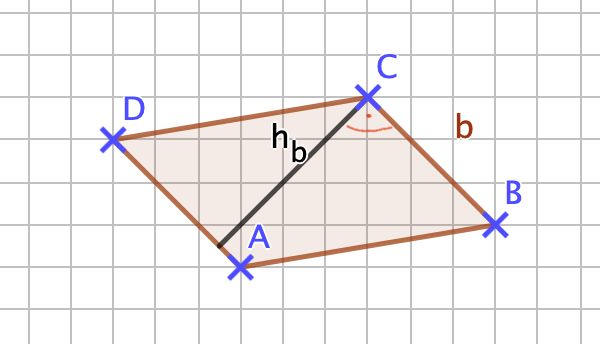
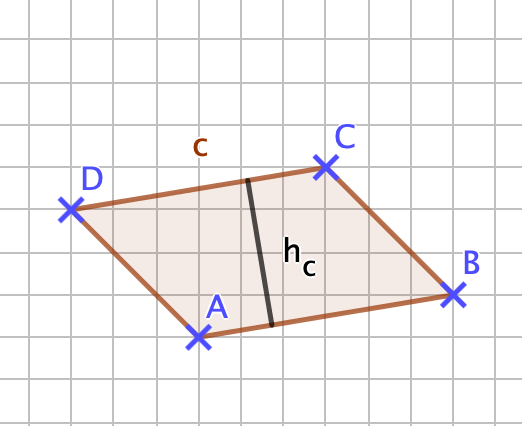
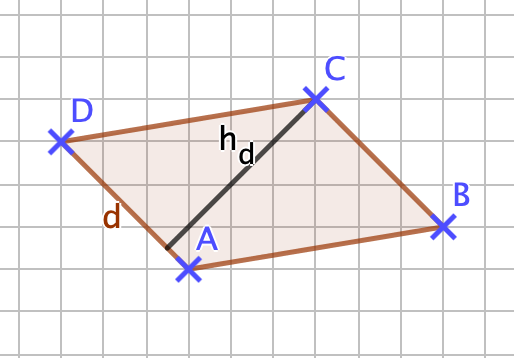
Der Abstand zwischen den parallelen Seiten des Parallelogramms wird als Höhe bezeichnet. Ein Parallelogramm hat zwei Höhen. Du zeichnest die Höhe, indem du eine Strecke rechtwinklig zu einer Seite zeichnest und diese mit der dazu parallelen Seite verbindest. | |Titel= ''' 4.1 Flächeninhalt eines Parallelogramms''' | ||
|Inhalt= Der Abstand zwischen den parallelen Seiten des Parallelogramms wird als Höhe bezeichnet. Ein Parallelogramm hat zwei Höhen. Du zeichnest die Höhe, indem du eine Strecke rechtwinklig zu einer Seite zeichnest und diese mit der dazu parallelen Seite verbindest. | |||
|Farbe= #CD2626 | |||
|Rahmen= 1 | |||
|Rahmenfarbe= #CD2626 | |||
}} | |||
|Farbe= #828282 | |||
|Rahmen= 1 | |||
|Rahmenfarbe= #828282 | |||
}} | |||
{{Box|Höhen im Parallelogramm zeichnen| | {{Box|Höhen im Parallelogramm zeichnen| | ||
Zeichne als erstes die Höhen in das Parallelogramm auf dem Arbeitsblatt und miss deren Längen. Vergleiche es mit der Lösung. | Zeichne als erstes die Höhen in das Parallelogramm auf dem Arbeitsblatt und miss deren Längen. Vergleiche es mit der Lösung. Falls du Schwierigkeiten damit hast, helfen dir die Bildfolgen im [https://projekte.zum.de/wiki/Buss-Haskert/Vierecke_und_Dreiecke/Umfang_und_Fl%C3%A4cheninhalt/Parallelogramm#1)_Höhen_im_Parallelogramm Original des Lernpfads.] | ||
{{Lösung versteckt|1= h<sub>a</sub>= | {{Lösung versteckt|1= h<sub>a</sub>=3cm und h<sub>b</sub>=3,6cm}} | ||
Zeichne ein beliebiges Parallelogramm in dein Merkeft und beschrifte die Seiten a und b. Zeichne nun die Höhen h<sub>a</sub> und h<sub>b</sub>. (Siehe z.B. S.139 Kasten)<br> | Zeichne ein beliebiges Parallelogramm in dein Merkeft und beschrifte die Seiten a und b. Zeichne nun die Höhen h<sub>a</sub> und h<sub>b</sub>. (Siehe z.B. S.139 Kasten)<br> | ||
Meist ist die eine Höhe leichter einzuzeichnen als die andere. | Meist ist die eine Höhe leichter einzuzeichnen als die andere. | ||
|Üben}} | |||
{{Box|1= | {{Box|1= Was fällt dir auf?|2= | ||
Verschiebe im nachfolgenden Applet die Punkte und beobachte die Lage der Höhen. Was fällt dir auf? | Verschiebe im nachfolgenden Applet die Punkte und beobachte die Lage der Höhen. Was fällt dir auf? Notiere auf dem Arbeitsblatt. | ||
<ggb_applet id="BkjVfyDh" width="800" height="600" /> | <ggb_applet id="BkjVfyDh" width="800" height="600" /> | ||
{{Lösung versteckt|Die Höhe eines Parallelogramms muss nicht immer im Parallelogramm selber liegen.|Idee öffnen|verbergen}} | {{Lösung versteckt|Die Höhe eines Parallelogramms muss nicht immer im Parallelogramm selber liegen.|Idee öffnen|verbergen}} | ||
}} | |||
Zeichne auf dem Arbeitsblatt jeweils beide Höhen in die beiden Parallelogramme ein.<br> | |||
Falls du Schwierigkeiten damit hast, helfen dir wieder die Bildfolgen im [https://projekte.zum.de/wiki/Buss-Haskert/Vierecke_und_Dreiecke/Umfang_und_Fl%C3%A4cheninhalt/Parallelogramm#1)_Höhen_im_Parallelogramm Original des Lernpfads.] | |||
{{Lösung versteckt|1= 1. Parallelogramm: h<sub>a</sub>=4,6cm und h<sub>b</sub>=4,5cm <br> | |||
2. Parallelogramm: h<sub>a</sub>=5,5cm oder 5,6 cm und h<sub>b</sub>=2,9cm oder 3 cm}} | |||
|3= Unterrichtsidee}} | |||
===Formeln herleiten: Flächeninhalt A und Umfang u=== | |||
{{Box|Idee| | {{Box|Idee| | ||
Nun versuche, mithilfe des GeoGebra-Applets die Formel für den Flächeninhalt des Parallelogramms herzuleiten. | Nun versuche, mithilfe des GeoGebra-Applets die Formel für den Flächeninhalt des Parallelogramms herzuleiten. Trage bei ? in die Kästchen ein. | ||
<ggb_applet id="V6CzmdBf" width="900" height="550" border="888888" /> | <ggb_applet id="V6CzmdBf" width="900" height="550" border="888888" /> | ||
<br> | <br> | ||
<br> | <br> | ||
Schaue dir auch das Rechteck und das Parallelogramm | Schaue dir auch das Rechteck und das Parallelogramm auf dem Arbeitsblatt an. Notiere deine Ideen auf dem Arbeitsblatt. | ||
|Unterrichtsidee}} | |||
{{#ev:youtube|wejTKC5_p8Y|800|center}}<br> | {{#ev:youtube|wejTKC5_p8Y|800|center}}<br> | ||
{{Box|1=Hefteintrag im Merkheft | {{Box|1=Hefteintrag im Merkheft | ||
|2=Flächeninhalt und Umfang des Parallelogramms<br> | |2=Flächeninhalt und Umfang des Parallelogramms<br> | ||
{{Lösung versteckt|1= | |||
Der Flächeninhalt A eines Parallelogramms ist gleich dem Produkt aus der Seitenlänge und der zugehörigen Höhe.<br> | Der Flächeninhalt A eines Parallelogramms ist gleich dem Produkt aus der Seitenlänge und der zugehörigen Höhe.<br> | ||
'''A = a∙h<sub>a</sub>''' oder '''A = b∙h<sub>b</sub>'''; allgemein: '''A = g∙h'''<br> | '''A = a∙h<sub>a</sub>''' oder '''A = b∙h<sub>b</sub>'''; allgemein: '''A = g∙h'''<br> | ||
Der Umfang | Der Umfang U eines Parallelogramms wird berechnet mit<br> | ||
''' | '''U = 2a + 2b''' oder '''U = 2(a + b)'''. | ||
|2=Merkhefteintrag abschreiben|3=verstecken}} | |||
|3=Arbeitsmethode}} | |||
{{#ev:youtube|PXiqKPhvzfQ|800|center}}<br> | {{#ev:youtube|PXiqKPhvzfQ|800|center}}<br> | ||
{{Box|Übung|Bearbeite die nachfolgenden Learningapps und das Applet.<br> Schreibe zur ersten App die Aufgaben dazu entsprechend der vorgegebenen Struktur ((1) geg. usw.) in dein Übungsheft.<br> | === Freitag, den 19.2.2021 === | ||
{{Box|Übung 1|Bearbeite die nachfolgenden Learningapps und das Applet.<br> Schreibe zur ersten App die Aufgaben dazu entsprechend der vorgegebenen Struktur ((1) geg. usw.) in dein Übungsheft.<br> | |||
In der zweiten App darfst du "nur" rechnen und auch im Geogebra-Applet gib "nur" das Ergebnis in das entsprechende Feld ein.|Üben}} | In der zweiten App darfst du "nur" rechnen und auch im Geogebra-Applet gib "nur" das Ergebnis in das entsprechende Feld ein.|Üben}} | ||
{{LearningApp|app=pp6ppcd6519|width=100%|height= | {{LearningApp|app=pp6ppcd6519|width=100%|height=800px}} | ||
{{LearningApp|app=pgc0vz74j19|width=100%|height=600px}} | {{LearningApp|app=pgc0vz74j19|width=100%|height=600px}} | ||
<ggb_applet id="nyxtebzk" width="900" height="520" border="888888" /> | <ggb_applet id="nyxtebzk" width="900" height="520" border="888888" /> | ||
{{Box|Übung|Bearbeite folgende Aufgaben im Übungsheft: | {{Box|1=Übung 2| 2= | ||
Berechne den Flächeninhalt der beiden Parallelogramme auf dem Arbeitsblatt und vergleiche mit der Lösung. | |||
{{Lösung versteckt|1= Eure Flächen können abweichen, da es sich beim Messen nicht um genaue Werte handelt. | |||
1. Parallelogramm: A = a*h<sub>a</sub> = 4,8cm * 4,6cm = 22,08 cm² oder A =b*h<sub>b</sub>= 4,9 cm * 4,5 cm = 22,05cm² <br> Die Flächen | |||
2. Parallelogramm: A= a*h<sub>a</sub>=3,9cm*5,5 cm = 21,45 cm² und A= b* h<sub>b</sub>=7,2cm*3cm = 21,6cm²|2= Lösung anzeigen|3=verstecken}} | |||
Das Arbeitsblatt ist nun ausgefüllt. Lade mir ein Bild davon hoch! | |||
|3=Üben}} | |||
{{Box|Übung 3|Bearbeite folgende Aufgaben im Übungsheft: | |||
*S. 140/5 | *S. 140/5 | ||
*S. 141/9a,b jeweils (1) bis (3) | *S. 141/9a,b jeweils (1) bis (3) | ||
| Zeile 68: | Zeile 101: | ||
|Üben}} | |Üben}} | ||
{{Box|Übung|Bearbeite folgende Aufgabe im Übungsheft: | {{Box|Übung 4|Bearbeite folgende Aufgabe im Übungsheft: | ||
*S. 142/17 | *S. 142/17 | ||
|Üben}} | |Üben}} | ||
== Mittwoch 24.2.2021== | |||
{{Box-spezial | |||
|Titel= '''<u>Guten Morgen!</u>''' | |||
|Inhalt= | |||
Bitte überprüft, ob ihr das Arbeitsblatt zum Parallelogramm ausgefüllt, schon abgegeben habt. Ansonsten holt es jetzt nach.<br> | |||
Jeder, der es abgegeben hat, liest bitte meine Anmerkungen und verbessert es gegebenenfalls.<br> | |||
Kontrolliert bitte eure Lösungen von Freitag mit der Lösung, die ihr im Modul Lernen findet. Auch hier kann es zu Abweichungen beim Messen und damit bei den Ergebnissen kommen. <br> | |||
|Farbe= #828282 | |||
|Rahmen= 1 | |||
|Rahmenfarbe= #828282 | |||
|Icon = <i class="fa fa-angellist" aria-hidden="true"></i> | |||
}} | |||
{{Box-spezial | |||
|Titel= Parallelogramm | |||
|Inhalt= | |||
* Zeichnet ein belibiges Parallelogramm auf ein Stück Papier (kann gerne auch bunt sein). | |||
* Zeichnet zwei Höhen zur Seite a ein, die jeweils in der Ecke des Parallelogramms enden. | |||
* Schneide das Parallelogramm aus. | |||
* Berechne den Flächeninhalt es Parallelogramms. | |||
|Farbe= #FF0000 | |||
|Rahmen= 1 | |||
|Rahmenfarbe= #FF0000 | |||
|Icon = <i class="fa fa-scissors" aria-hidden="true"></i> | |||
}} | |||
{{Box|1=Überlegung|2= | |||
'''Wie gut haben die Aufgaben S.141/9 und 10 letzte Woche funktioniert?''' <br> | |||
<br> | |||
♦ 1) Noch nicht so gut. Ich würde das gerne noch einmal üben.<br> | |||
<br> | |||
♦ 2) Super gut. Ich hatte (fast) alles richtig. Ich bin fit bei diesem Thema.<br> | |||
<br> | |||
|3=Frage}} | |||
{{Box|1=Info|2= Hast du Antwort 1) gewählt, bearbeite Variante 1. Hast du 2) gewählt bearbeite Variante 2. | |||
|3=Kurzinfo}} | |||
{{Box|1=Variante 1|2= | |||
Lies noch einmal im Merkheft nach, was die Höhe des Parallelogramms ist. <br> | |||
{{2Spalten| | |||
{{Box| Einzeichnen der Höhen - 1: |{{#ev:youtube|watch?v=WULo-g3PBPQ|400|center}} | Hervorhebung1}}| | |||
{{Box| Einzeichnen der Höhen - 2: |{{#ev:youtube|watch?v=jRXu-vDyK3k|400|center}} | Hervorhebung1}} | |||
}} | |||
Das brauchen wir um den Flächeninhalt zu berechnen.<br> | |||
Notiere die auch die Formel zu Berechnung des Flächeninhalts. <br> | |||
<br> | |||
Bearbeite im Übungsheft die folgenden Aufgaben. Verbessere immer erst, bevor du weiter machst. | |||
*''' S.141/6''' Gehe hier Zeile für Zeile vor und vergleiche | |||
{{Lösung versteckt|1=[[Datei:141-6-1.png]]<br>Wenn du richtig gezeichnet hast, dann müsste die Seite <math>\bar{AB}</math> ca. 3cm sein und die zugehörige Höhe ca. 1,7cm. Der Flächeninhalt ist dann: A=3cm•1,7cm=5,1cm² <br> | |||
Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 1 Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:141-6-2.png]]<br>Die Länge der Seite b ist ca. 2,1cm die zugehörige Höhe ist ca. 2,5cm. Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 2 Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:141-6-4.png]]<br>Die Länge der Seite c ist ca. 3cm (Denn sie ist ja parallel zur Seite a) die zugehörige Höhe ist dann ebenfalls wieder ca. 1,7cm. Mit diesen Werten kommt man auf einen Flächeninhalt von 5,1cm². |2=Zeile 3 Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:141-6-3.png]]<br>Die Länge der Seite d ist ca. 2,1cm (denn sie ist parallel zu b) die zugehörige Höhe ist ca. 2,5cm. Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². <br> | |||
Unterschiede im Flächeninhalt entstehen aufgrund von Messungenauigkeiten. Eigentlich sollte bei jeder Messung und Rechnung immer der gleiche Flächeninhalt herauskommen. |2=Zeile 4 Aufdecken|3=Verbergen}} | |||
* '''S.141/10c,d''' Überlege vor dem Zeichnen, was die x und was die y-Achse ist. Wenn du es nicht mehr weißt, lies im Grundwissen nach. Denke daran, dass wir die Höhe beim Berechnen brauchen. | |||
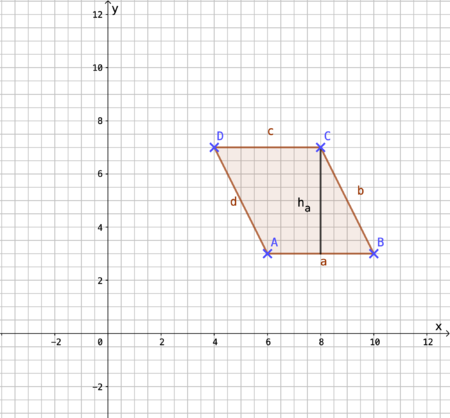
{{Lösung versteckt|1=[[Datei:141-10c.png|141-10c.png|450px]]A=a•h<sub>a</sub> = 4cm•4cm=16cm² |2=10c Aufdecken|3=Verbergen}} | |||
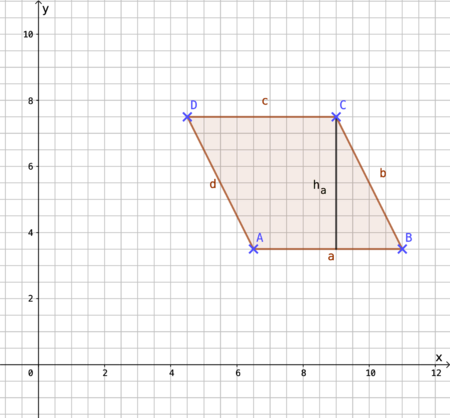
{{Lösung versteckt|1=[[Datei:141-10d.png|141-10d.png|450px]]A=a•h<sub>a</sub> = 4,5cm•4cm=18cm² |2=10d Aufdecken|3=Verbergen}} | |||
* '''S.142/12a,b,c''' | |||
{{Lösung versteckt|1=[[Datei:141-12a.jpg|141-12a.jpg]] |2=12a Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:141-12b.jpg|141-12b.jpg]] |2=12b Aufdecken|3=Verbergen}} | |||
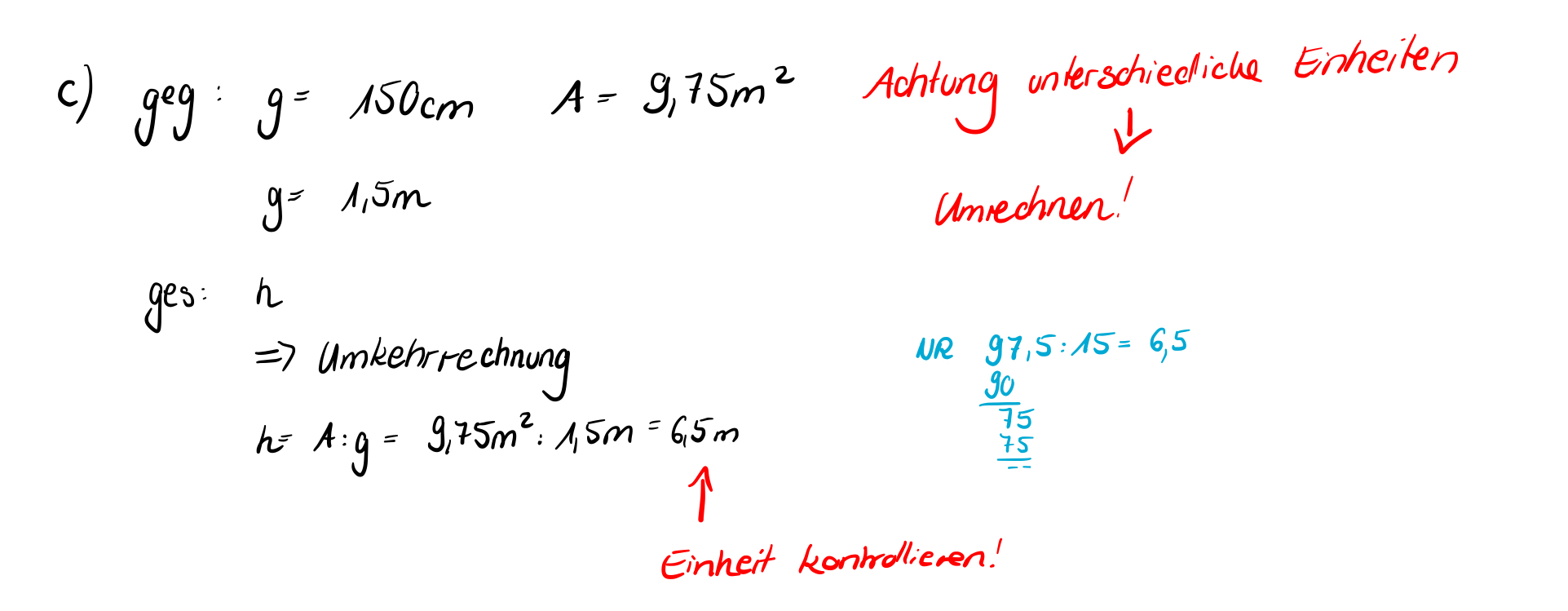
{{Lösung versteckt|1=[[Datei:141-12c.jpg|141-12c.jpg]] |2=12c Aufdecken|3=Verbergen}} | |||
Wenn du noch keine 45min gearbeitet hast, dann springe ans Ende und bearbeite noch die Apps zum Rechnen mit Längeneinheiten. | |||
|3=Arbeitsmethode}} | |||
{{Box|1=Variante 2|2= | |||
Bearbeite im Übungsheft die folgenden Aufgaben. Verbessere immer erst, bevor du weiter machst. | |||
*'''S.142/12a,b,c''' | |||
{{Lösung versteckt|1=[[Datei:141-12a.jpg|141-12a.jpg]] |2=12a Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:141-12b.jpg|141-12b.jpg]] |2=12b Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:141-12c.jpg|141-12c.jpg]] |2=12c Aufdecken|3=Verbergen}} | |||
*'''S.142/15''' | |||
{{Lösung versteckt|1= <br> | |||
a) (1) Der Flächeninhalt verdoppelt sich. (2) Der Flächeninhalt verdreifacht sich. <br> | |||
b) (1) Der Flächeninhalt vervierfacht sich. (2) Der Flächeninhalt versechsfacht sich. <br> | |||
|2=142/15 Aufdecken|3=Verbergen}} | |||
*'''S.142/16''' | |||
{{Lösung versteckt|1= | |||
Berechne erst den Flächeninhalt A = a•h<sub>a</sub> =5,7cm •2,5cm = 14,25cm² ; <br> | |||
Dann die Höhe von b mit einer Umkehrrechnung h<sub>b</sub> = A:b = 14,25cm²:3,5cm ≈ 4,1cm.|2=142/16 Aufdecken|3=Verbergen}} | |||
Wenn du noch keine 45min gearbeitet hast, dann springe ans Ende und bearbeite noch die Apps zum Rechnen mit Längeneinheiten. | |||
|3=Arbeitsmethode}} | |||
{{Box |1= Zur Wiederholung:|2= Und nun noch etwas Umrechnen von Einheiten <br> | |||
{{LearningApp|app=11240926|width=100%|height=700px}} | |||
|3=Üben}} | |||
{{Box |1= Zur Wiederholung:|2= Und nun noch etwas Umrechnen von Einheiten - ein paar Flächeneinheiten... <br> {{LearningApp|app=pfhyzuzvn21|width=100%|height=700px}} | |||
|3=Üben}} | |||
Aktuelle Version vom 22. Februar 2021, 13:10 Uhr
4.1 Das Parallelogramm
Lies im Merkheft zur Wiederholung das "Haus der Vierecke" durch. In Anton kannst du im Pin "Figuren" mit den ersten beiden Übungen die Eigenschaften der ebsonderen Vierecke wiederholen. Nicht mehr bearbeiten.
Parallelogrammen und Rechteck
Bearbeite auf dem Arbeitsblatt die Aufgaben 1 und 2.
Höhe im Parallelogramm
Notiere in dein Merkheft:
Formeln herleiten: Flächeninhalt A und Umfang u
Freitag, den 19.2.2021

Mittwoch 24.2.2021