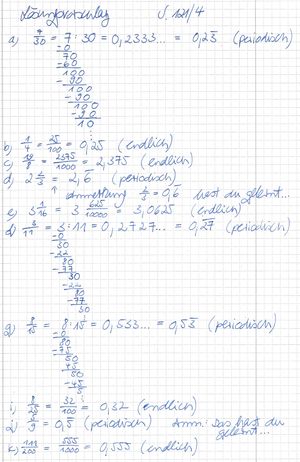6e Lernen zu Hause: Dezimalbrüchen: Unterschied zwischen den Versionen
Aus RMG-Wiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 235: | Zeile 235: | ||
{{Lösung versteckt |1= Lösung der Aufgaben: <br> | {{Lösung versteckt |1= Lösung der Aufgaben: <br> | ||
Allgemeine Info zu Aufgabe 3: <br> In der Regel ist das Addieren und Subtrahieren von Dezimalbrüchen | Allgemeine Info zu Aufgabe 3: <br> In der Regel ist das Addieren und Subtrahieren von Dezimalbrüchen schneller. <br> In b), c), g), h) und j) kann man die Brüche nicht in endliche Dezimalbrüche umwandeln. Daher rechnet man hier mit Brüchen! <br> | ||
'''a)''' <br> | '''a)''' <br> | ||
<math>0,2 + 0,75 = 0,95 </math> oder aber auch | <math>0,2 + 0,75 = 0,95 </math> oder aber auch | ||
<math>\frac {2}{10} + \frac {3}{4} = \frac {19}{20}</math> <br> | <math>\frac {2}{10} + \frac {3}{4} = \frac{4}{20} + \frac{15}{20} = \frac {19}{20}</math> <br> | ||
'''b)''' <br> | '''b)''' <br> | ||
| Zeile 248: | Zeile 248: | ||
'''d)''' <br> | '''d)''' <br> | ||
<math> 0,75 - \frac{1}{4} = 0,75 - 0,25 = 0,5 </math> oder aber auch | <math> 0,75 - \frac{1}{4} = 0,75 - 0,25 = 0,5 </math> oder aber auch | ||
<math> 0,75 - \frac{1}{4} = \frac{3}{4} - \frac{1}{4} = \frac{2}{4}= \frac {1}{2} </math> <br> | <math> 0,75 - \frac{1}{4} = \frac{3}{4} - \frac{1}{4} = \frac{2}{4}= \frac {1}{2} </math> <br> | ||
'''e)''' <br> | '''e)''' <br> | ||
<math> \frac{1}{8} + 0,75 = 0,125 + 0,75 = 0,875 </math> oder aber auch | <math> \frac{1}{8} + 0,75 = 0,125 + 0,75 = 0,875 </math> oder aber auch | ||
<math> \frac{1}{8} + 0,75 = \frac {1}{8} + \frac{3}{4} = \frac{1}{8} + \frac{6}{8} = \frac{7}{8} </math> <br> | <math> \frac{1}{8} + 0,75 = \frac {1}{8} + \frac{3}{4} = \frac{1}{8} + \frac{6}{8} = \frac{7}{8} </math> <br> | ||
'''f)''' <br> | '''f)''' <br> | ||
<math> \frac{1}{8} + 0,7 = 0,125 + 0,7 = 0, | <math> \frac{1}{8} + 0,7 = 0,125 + 0,7 = 0,825 </math> oder aber auch | ||
<math> \frac{1}{8} + 0,7 = \frac{1}{8} + \frac{7}{10} = \frac{5}{40} + \frac{28}{40} = \frac{33}{40} </math> <br> | <math> \frac{1}{8} + 0,7 = \frac{1}{8} + \frac{7}{10} = \frac{5}{40} + \frac{28}{40} = \frac{33}{40} </math> <br> | ||
| Zeile 266: | Zeile 266: | ||
'''i)''' <br> | '''i)''' <br> | ||
<math> 0,9 -\frac{3}{25}= 0,9 - \frac{12}{100} = 0,9 - 0,12 = 0,78 </math> oder aber auch | <math> 0,9 -\frac{3}{25}= 0,9 - \frac{12}{100} = 0,9 - 0,12 = 0,78 </math> oder aber auch | ||
<math> 0,9 - \frac{3}{25} = \frac{9}{10} - \frac{3}{25} = \frac{45}{50} - \frac{6}{50} = \frac{39}{50} </math> <br> | <math> 0,9 - \frac{3}{25} = \frac{9}{10} - \frac{3}{25} = \frac{45}{50} - \frac{6}{50} = \frac{39}{50} </math> <br> | ||
| Zeile 277: | Zeile 277: | ||
'''a)''' <br> | '''a)''' <br> | ||
Jonas hat mit Brüchen und Linda mit Dezimalbrüchen gerechnet. <br> | |||
'''b)''' <br> | '''b)''' <br> | ||
<math>\frac{ | |||
(1) <math> 15 \cdot 0,7 l = 10,5 l </math> oder <math> 15 \cdot \frac{7}{10} l = \frac { 15 \cdot 7}{10} l = \frac{105}{10} l = 10 \frac{5}{10} l = 10 \frac{1}{2} l </math> <br> Im Keller befinden sich insgesamt 10,5 l Wasser. <br> | |||
(2) <math>4 \cdot \frac{3}{8} l = \frac { 4 \cdot 3}{8} l = \frac{3}{2} l </math> oder <math> 4 \cdot \frac {3}{8} l = 4 \cdot \frac{375}{1000} l = 4 \cdot 0,375 l = 1,5 l </math> <br> Für die vier Kuchen benötigt Franziska 1,5 Liter Sahne. <br> | |||
|2= Lösung der Aufgabe 5 anzeigen | 3= Lösung verbergen}} <br> | |2= Lösung der Aufgabe 5 anzeigen | 3= Lösung verbergen}} <br> | ||
|3= | |3= Üben}} | ||
{{Box |1= Freiwillig: |2= Falls du noch Lust hast, kannst du hier nochmal die Zusammenhänge zwischen Brüchen, Dezimalzahlen und Prozentzahlen wiederholen. <br> {{LearningApp|app=1574798|width=100%|height=700px}} | |||
|3= Arbeitsmethode}} | |||
Aktuelle Version vom 8. Februar 2021, 09:31 Uhr
08.02.2021
10.02.2021
11.02.2021