Einführung in die Negativen Zahlen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
K (1 Version importiert) |
(kein Unterschied)
| |
Version vom 19. April 2020, 09:47 Uhr
Eine Unterseite beginnt mit einem einführenden Video. Anschließend folgt eine Frage, die dem Abschnitt als Leitfrage dient. Weiterhin findet ihr Aufgaben, die mit folgenden Icons gekennzeichnet sind:
Technische Hinweise
Videos:
Im Laufe des Lernpfades werdet ihr immer wieder auf Videos treffen. Diese könnt ihr natürlich pausieren und so oft anschauen, wie ihr möchtet. Außerdem könnt ihr sie auch im Vollbildmodus abspielen. Die Videos haben keinen Ton.
Learning Apps: Im Laufe des Lernpfades werdet ihr auf sogenannte Learning Apps treffen. Für eine angenehmere Optik wurden sie manchmal etwas verkleinert. Wenn euch das zu klein ist, könnt ihr bei jeder Learning App den Vollbild-Modus aktivieren, indem ihr auf das kleine Symbol oben rechts in dem Applet klickt.
Didaktische Hinweise für die Lehrkraft
Dieser Lernpfad ist entsprechend des Gymnasiallehrplanes in Sachsen zur Einführung der negativen Zahlen im LB 2: "Arbeiten mit rationalen Zahlen" in Klasse 7 angelegt.
Vorkenntnisse
Zur Nutzung dieses Lernpfades sind folgende Vorkenntnisse der Schülerinnen und Schüler erforderlich:
- Die SuS kennen die Mengen "natürliche Zahlen" und "gebrochene Zahlen".
- Die SuS können natürliche und gebrochene Zahlen am Zahlenstrahl abtragen.
- Die SuS können natürliche und gebrochene Zahlen vergleichen und ordnen.
Wissensziele
- Die SuS kennen den Alltagsbezug negativer Zahlen.
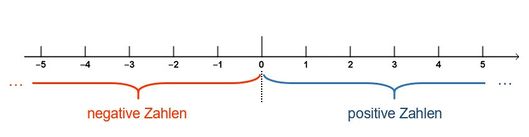
- Die SuS beherrschen das Darstellen und Ablesen negativer Zahlen an der Zahlengerade.
- Die SuS kennen die Begriffe "entgegengesetzte Zahl" und "Betrag".
- Die SuS können negative Zahlen vergleichen und ordnen.
Einsatz
Die Schülerinnen und Schüler arbeiten alleine oder mit einem Partner. Wenn der Lernpfad in Einzelarbeit durchgeführt wird, kann bei Partnerarbeitsaufgaben die Busstop-Methode eingesetzt werden.
Der Lernpfad ist momentan in der Erprobungsphase, weshalb noch kein Zeitumfang angegeben werden kann.