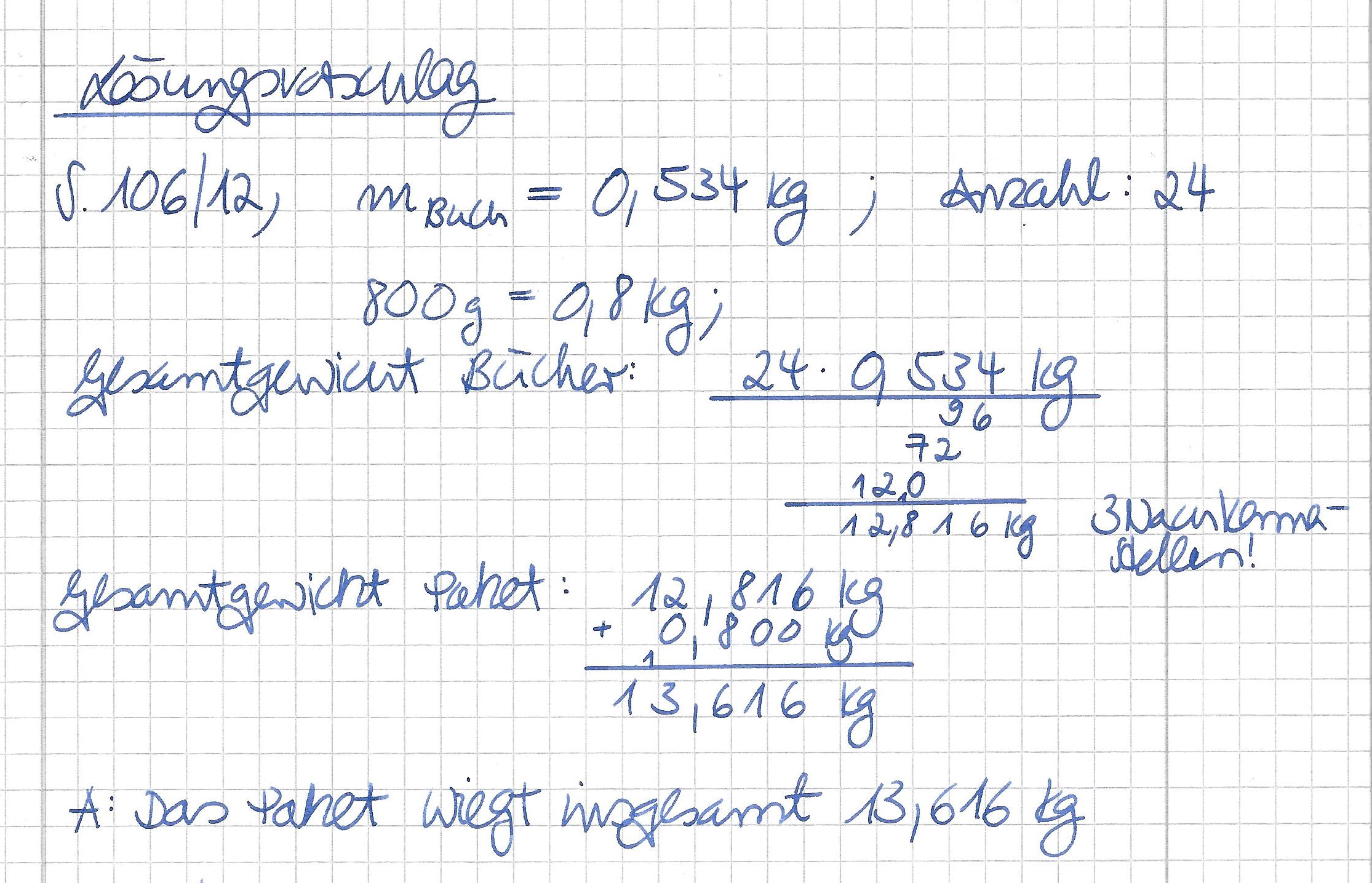6d 2024 25/Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (14 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 244: | Zeile 244: | ||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
= | =10.03.2025: Hausaufgabe - Zur Wiederholung = | ||
{{Box |1= Wiederholung: |2= Fasse mündlich noch einmal für dich zusammen, was ein endlicher Dezimalbruch ist und wie er entsteht! <br> Definiere, was ein periodischer Dezimalbruch ist, wie ist hierbei die Notation! <br> Lerne den Zusammenhang zwischen Brüchen mit Nenner 9 und ihren periodischen Dezimalbrüchen! <br> | {{Box |1= Wiederholung: |2= Fasse mündlich noch einmal für dich zusammen, was ein endlicher Dezimalbruch ist und wie er entsteht! <br> Definiere, was ein periodischer Dezimalbruch ist, wie ist hierbei die Notation! <br> Lerne den Zusammenhang zwischen Brüchen mit Nenner 9 und ihren periodischen Dezimalbrüchen! <br> | ||
|3= Üben}} | |3= Üben}} | ||
{{Box |1= | {{Box |1= LERNE!! - Brüche mit Nenner 9: |2= Bitte keine Panik, das ist nicht so viel, wie es auf den ersten Blick wirkt, du erkennst sicherlich ein Schema beim Lernen und denke bitte immer an die Möglichkeit des '''Kürzens''', das erklärt doch auch so einiges... | ||
| Zeile 268: | Zeile 268: | ||
|3= Merksatz}} | |3= Merksatz}} | ||
{{Box |1= Test:|2= Zum Überprüfen und weiteren Vertiefen deines gelernten Wissens kannst du hier '''freiwillig''' noch einmal Paare von Brüchen und Dezimalbrüchen passend zuordnen. Mit der folgenden LearningApp hast du die Möglichkeit zu testen, ob du besondere Brüche und ihre zugehörigen Dezimalzahlen bereits gut genug gelernt hast. Viel Freude dabei! <br> | {{Box |1= Test:|2= Zum Überprüfen und weiteren Vertiefen deines gelernten Wissens kannst du hier '''freiwillig''' noch einmal Paare von Brüchen und Dezimalbrüchen passend zuordnen. Mit der folgenden LearningApp hast du die Möglichkeit zu testen, ob du besondere Brüche und ihre zugehörigen Dezimalzahlen bereits gut genug gelernt hast. Viel Freude dabei! <br> {{LearningApp|app=ppjjvkti321|width=100%|height=700px}} | ||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
{{Box |1= Test: |2= Zur Wiederholung und Vertiefung: Endlich oder unendlicher Bruch? Sortiere jeweils zu! Kürzen bzw. Erweitern auf 10, 100, 1000, 10000, ... kann dir dabei helfen endliche Brüche "herauszuangeln..." <br> {{LearningApp|app=8373214|width=100%|height=700px}} | {{Box |1= Test: |2= Zur Wiederholung und Vertiefung: Endlich oder unendlicher Bruch? Sortiere jeweils zu! Kürzen bzw. Erweitern auf 10, 100, 1000, 10000, ... kann dir dabei helfen endliche Brüche "herauszuangeln..." <br> {{LearningApp|app=8373214|width=100%|height=700px}} | ||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
=25.03.2025: Hausaufgabe zu Parallelogramm und Wiederholung zu Einheiten = | |||
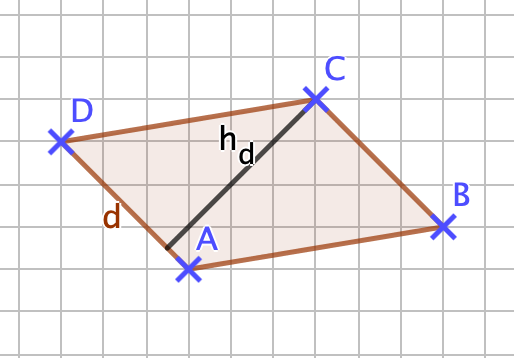
{{Box |1= Erinnerung: |2= Zur Berechnung des Flächeninhalts eines Parallelogramms benötigt man, wie du weißt, die Höhen im Parallelogramm. Mit folgender Darstellung kannst du erkennen, wie die Höhe im Parallelogramm dargestellt wird. Verschiebe die blauen Punkte des Parallelogramms mit deiner Maus und beobachte dabei, wann sich die Höhen innerhalb bzw. außerhalb des Parallelogramms befinden und wie man diese einzeichnet. <br> | |||
<ggb_applet id="BkjVfyDh" width="800" height="600" /> | |||
<br> | |||
<br> | |||
|3= Unterrichtsidee}} | |||
{{Box|Hinweis:| | |||
{{Lösung versteckt|1= | |||
'''Höhen im Parallelogramm'''<br> | |||
Unter den Höhen eines Parallelogramms versteht man die Abstände der zueinander parallelen Seiten des Parallelogramms. Ein Parallelogramm hat zwei Höhen. <br> | |||
Man zeichnet die Höhe, indem man eine Strecke rechtwinklig zu einer Seite zeichnest und diese mit der dazu parallelen Seite verbindest. | |||
<br> | |||
|2=Aufdecken|3=Verbergen}} | |||
|3=Merksatz}} | |||
{{Box| FREIWILLIG - Einzeichnen der Höhen - 1: |{{#ev:youtube|WULo-g3PBPQ}} | Hervorhebung1}} | |||
{{Box| FREIWILLIG - Einzeichnen der Höhen - 2: |{{#ev:youtube|jRXu-vDyK3k}} | Hervorhebung1}} | |||
{{Box |1= Übung - Berechnung des Flächeninhalts von Parallelogrammen:|2= Nun darfst du selbst die Höhe suchen.... und hoffentlich finden! Falls das noch nicht so gut klappen sollte, nochmal der Hinweis auf die freiwilligen Videos vorab zum Zeichnen der Höhen beim Parallelogramm. <br> {{LearningApp|app=pgc0vz74j19|width=100%|height=600px}} | |||
|3= Arbeitsmethode}} | |||
{{Box |1= Zur Wiederholung:|2= Zum Abschluss der heutigen Hausaufgabe noch etwas Umrechnen von Einheiten - zunächst Längeneinheiten... Du musst hier nicht alle Aufgaben bearbeiten, sollten dir die einfachen zu einfach sein, dann lass sie bitte einfach weg, die zu "schwieriger" sind jedoch Pflicht! <br> | |||
Zum Reinkommen in das Umrechnen von Einheiten können die "einfachen" Aufgaben aber auch hilfreich sein, dies entscheidest du aber vollkommen selbstständig, je nachdem, wie gut du dich noch an das Umrechnen von Einheiten erinnern kannst!<br> {{LearningApp|app=11240926|width=100%|height=700px}} <br>|3= Arbeitsmethode}} | |||
{{Box |1= Zur Wiederholung:|2= Und nun noch etwas Umrechnen von Einheiten - ein paar Flächeneinheiten... <br> {{LearningApp|app=pfhyzuzvn21|width=100%|height=700px}} <br> |3= Arbeitsmethode}} | |||
=28.03.2025: Hausaufgabe = | |||
{{Box |1= Übung: |2= Bevor du startest wiederhole bitte für dich die Formel zur Berechnung des Flächeninhalts eines Parallelogramms und auch die Formel zur Berechnung seines Umfangs. <br> | |||
Bearbeite bitte im Buch S. 141/ 6! <br> | |||
Berechne Zeile für Zeile und verbessere immer direkt im Anschluss deine Lösung mit dem folgenden Lösungsvorschlag. <br> Lass dich nicht irritieren, du fertigst im Heft nur eine Skizze des Parallelogramms an - hier ist für jede Zeile eine Skizze angefügt, dies dient der besseren Übersichtlichkeit und Nachvollziehbarkeit der Lösung. | |||
{{Lösung versteckt|1=[[Datei:141-6-1.png]]<br>Wenn du richtig gezeichnet hast, dann müsste die Seite <math>\overline{AB} = a </math> ca. 3cm sein und die zugehörige Höhe ca. 1,7cm. <br> Der Flächeninhalt ist dann: A=3cm•1,7cm=5,1cm² <br> | |||
Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 1 Aufdecken|3=Verbergen}} | |||
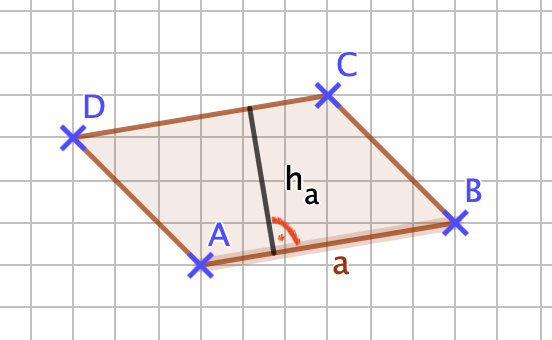
{{Lösung versteckt|1=[[Datei:141-6-2.png]]<br>Die Länge der Seite <math> \overline{BC} = b </math> ist ca. 2,1cm die zugehörige Höhe ist ca. 2,5cm. <br> Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 2 Aufdecken|3=Verbergen}} | |||
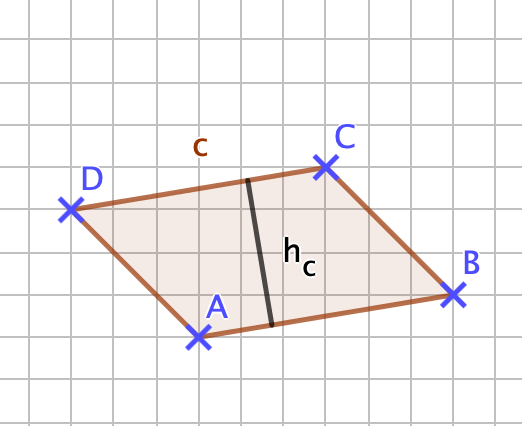
{{Lösung versteckt|1=[[Datei:141-6-4.png]]<br>Die Länge der Seite <math> \overline{CD} = c </math> ist ca. 3cm, c =a! Die zugehörige Höhe ist dann ebenfalls, wie auch die Höhe zur Seite a, ca. 1,7cm. <br> Mit diesen Werten kommt man auf einen Flächeninhalt von 5,1cm². |2=Zeile 3 Aufdecken|3=Verbergen}} | |||
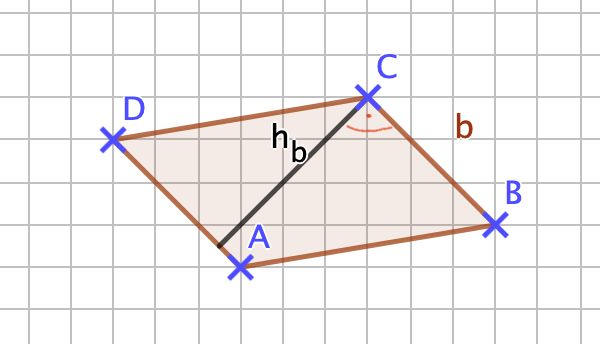
{{Lösung versteckt|1=[[Datei:141-6-3.png]]<br>Die Länge der Seite <math> \overline{DA} = d </math> ist ca. 2,1cm, d = b! Die zugehörige Höhe ist, wie auch die Höhe zur Seite b, ca. 2,5cm. Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². <br> | |||
'''Feststellung und Begründung:''' | |||
Unterschiede im Flächeninhalt entstehen aufgrund von Messungenauigkeiten. Eigentlich sollte bei jeder Messung und Rechnung immer der gleiche Flächeninhalt herauskommen, die Fläche des Parallelogramms verändert sich ja nicht.... |2=Zeile 4 Aufdecken|3=Verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Übung: |2= Bearbeite B. S. 142/ 12 b), c)! <br> Vergiss nicht die Anwendungsmöglichkeit einer Umkehrrechnung... | |||
{{Lösung versteckt |1= '''Lösung der Aufgaben:''' <br> | |||
'''b)''' <br> | |||
h = 5,2 cm und A = 22,36 cm² <br> Löse mit der Umkehraufgabe: <br> | |||
<math> g= A \div h = 22,36 cm^2 \div 5,2 cm = 223,6 cm^2 \div 52 cm = 4,3 cm </math> <br> Vergiss bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! | |||
'''c)''' <br> | |||
Am besten du rechnest beide Größen sofort in dieselbe Einheit um! <br> g = 150 cm und A = 9,75 m² = 975 dm² = 97500 cm² <br> Löse mit der Umkehraufgabe: <br> | |||
<math> h= A \div g = 97500 cm^2 \div 150 cm = 650 cm = 6,5 m </math> <br> Vergiss auch hier bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! | |||
|2= Lösung anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
Version vom 25. März 2025, 16:18 Uhr
31.01.2025: Übungen zu Multiplizieren mit Stufenzahlen und Dividieren durch Stufenzahlen
Zur Vorbereitung zu Hause auf die kommende Stunde - Multiplizieren von Dezimalbrüchen
03.02.25: Weiter geht es mit dem Multiplizieren von Dezimalbrüchen
14.02.2025: Dividieren von Dezimalbrüchen und Hausaufgabe zum Multiplizieren von Dezimalbrüchen
18.02.2025: Hausaufgabe
10.03.2025: Hausaufgabe - Zur Wiederholung
25.03.2025: Hausaufgabe zu Parallelogramm und Wiederholung zu Einheiten