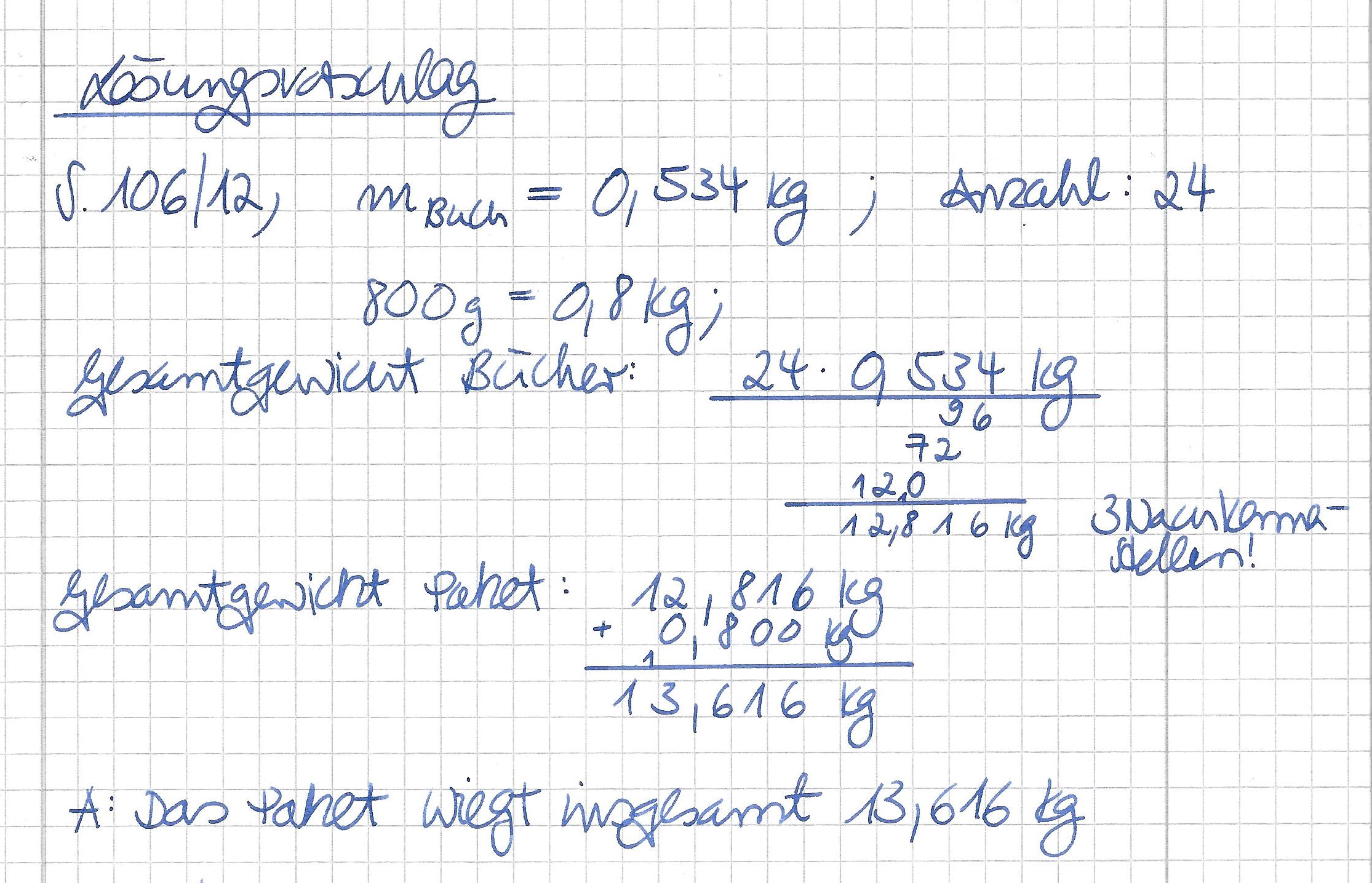6d 2024 25/Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (31 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 72: | Zeile 72: | ||
=Multiplizieren von Dezimalbrüchen= | =Zur Vorbereitung zu Hause auf die kommende Stunde - Multiplizieren von Dezimalbrüchen= | ||
{{Box|1= Neu: |2= Nicht verrückt machen, wenn du Schriftlich Multiplizieren und auch noch zählen kannst, sollte das Multiplizieren von Dezimalbrüchen kein Problem werden. <br> Notiere dir zunächst die Überschrift "Multiplizieren | {{Box|1= Neu: |2= Nicht verrückt machen, wenn du Schriftlich Multiplizieren und auch noch zählen kannst, sollte das Multiplizieren von Dezimalbrüchen kein Problem werden. <br> Notiere dir zunächst die Überschrift "Multiplizieren von Dezimalbrüchen" mit dem heutigen Datum in dein Heft! <br> | ||
Sieh dir nun das folgende Video aufmerksam an!| 3= Arbeitsmethode}} | |||
{{Box| Multiplizieren von Dezimalbrüchen:|{{#ev:youtube|2QfdWJMQpUU}}|Hervorhebung1}}{{Box |1= Zur Kontrolle: |2= Nun bist du an der Reihe! Berechne nun nochmal alleine die beiden Aufgaben aus dem Video! | {{Box| Multiplizieren von Dezimalbrüchen:|{{#ev:youtube|2QfdWJMQpUU}}|Hervorhebung1}} | ||
{{Box |1= Zur Kontrolle: |2= Nun bist du an der Reihe! Berechne nun nochmal alleine die beiden Aufgaben aus dem Video! | |||
*Berechne <math> 8,3 \cdot 1,4 </math>! | *Berechne <math> 8,3 \cdot 1,4 </math>! | ||
| Zeile 93: | Zeile 95: | ||
# Multipliziere zunächst so, als wäre kein Komma vorhanden - Stichwort: schriftlich Multiplizieren! | # Multipliziere zunächst so, als wäre kein Komma vorhanden - Stichwort: schriftlich Multiplizieren! | ||
# Setze dann im Ergebnis das Komma so, dass rechts vom Komma so viele Zahlen stehen, wie die beiden Faktoren zusammen nach dem Komma haben! | # Setze dann im Ergebnis das Komma so, dass rechts vom Komma so viele Zahlen stehen, wie die beiden Faktoren zusammen nach dem Komma haben! | ||
|3= Merksatz}}{{Box |1= Zur Vertiefung: |2= Berechne folgende Aufgaben! | |3= Merksatz}} | ||
=03.02.25: Weiter geht es mit dem Multiplizieren von Dezimalbrüchen= | |||
{{Box |1= Zur Vertiefung: |2= Berechne folgende Aufgaben! | |||
*B.S.106/ 19 a): Berechne <math> 30,8 \cdot 0,29 </math>! | *B.S.106/ 19 a): Berechne <math> 30,8 \cdot 0,29 </math>! | ||
| Zeile 107: | Zeile 112: | ||
{{Lösung versteckt|1= <math> = 27,2288 </math> <br> WICHTIG: Berechne zunächst schriftlich <math> 508 \cdot 536 </math>. Das Ergebnis hier ist 272288. <br> Die Zahl 0,508 hat drei Nachkommastellen, die Zahl 53,6 hat eine Nachkommastelle. <br> Da "3 Nachkommastellen + 1 Nachkommastelle = 4 Nachkommastellen", hat das Ergebnis der Multiplikation vier Nachkommastellen... |2=Aufdecken|3=Verbergen}} | {{Lösung versteckt|1= <math> = 27,2288 </math> <br> WICHTIG: Berechne zunächst schriftlich <math> 508 \cdot 536 </math>. Das Ergebnis hier ist 272288. <br> Die Zahl 0,508 hat drei Nachkommastellen, die Zahl 53,6 hat eine Nachkommastelle. <br> Da "3 Nachkommastellen + 1 Nachkommastelle = 4 Nachkommastellen", hat das Ergebnis der Multiplikation vier Nachkommastellen... |2=Aufdecken|3=Verbergen}} | ||
|3= Üben}}{{Box|1= Übung:| 2= Bearbeite bitte folgende Aufgaben im Schulheft: B. S. | |3= Üben}}{{Box|1= Übung:| 2= Bearbeite bitte folgende Aufgaben im Schulheft: B. S. 106/ 12, 15 und 17 b) | ||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag 106 12.jpg]] |2= Lösung Aufgabe 12 anzeigen | 3= Lösung verbergen}} | {{Lösung versteckt |1=[[Datei:Lösungsvorschlag 106 12.jpg]] |2= Lösung Aufgabe 12 anzeigen | 3= Lösung verbergen}} | ||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag 106 15.jpg]] |2= Lösung Aufgabe 15 anzeigen | 3= Lösung verbergen}} | {{Lösung versteckt |1=[[Datei:Lösungsvorschlag 106 15.jpg]] |2= Lösung Aufgabe 15 anzeigen | 3= Lösung verbergen}} | ||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag 106 17b.jpg]] |2= Lösung Aufgabe 17 b) anzeigen | 3= Lösung verbergen}} | {{Lösung versteckt |1=[[Datei:Lösungsvorschlag 106 17b.jpg]] |2= Lösung Aufgabe 17 b) anzeigen | 3= Lösung verbergen}} | ||
|3= Üben}} | |||
{{Box| 1= Zur Vertiefung: | | |||
2= Notiere in der Lösungszeile nur die Zahl, die in die gelb markierte Lücke notiert werden muss, beachte dabei auch die "Gemerkten". <br> | |||
{{LearningApp|app=12302944|width=100%|height=700px}} | |||
|3 = Arbeitsmethode}} | |||
{{Box| 1= Nun noch etwas Kopfrechnen...: | | |||
2= {{LearningApp|app=4293413|width=100%|height=700px}} | |||
|3 = Arbeitsmethode}} | |||
{{Box|1= Kommaverschiebung für Produkte: |2= Bearbeite bitte B. S. 104/ 2! Übertrage bitte auch den roten Kasten als Merksatz in dein Schulheft während du die Aufgabe bearbeitest ! | |||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag B S 104 2.jpg]] |2= Lösung Aufgabe 2 anzeigen | 3= Lösung verbergen}} | |||
| 3= Arbeitsmethode}} | |||
{{Box|1= Übung: |2= Bearbeite bitte B. S. 105/ 7 b), c) und 11! | |||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag B S 105 7b c 11.jpg|Lösungsvorschlag B S 105 7b c 11.jpg]] |2= Lösung Aufgabe 7 und 11 anzeigen | 3= Lösung verbergen}} | |||
| 3= Arbeitsmethode}} | |||
{{Box| 1= '''FREIWILLIG:''' |2 = Falls du noch Energie hast, kannst du hiermit nochmal das Multiplizieren von Dezimalbrüchen üben...nimm dir bitte für Nebenrechnungen einen Stift und dein Heft zur Hand, das Erraten der Lösungen bringt leider nicht sehr viel... <br> {{LearningApp|app=3095700|width=100%|height=700px}} | |||
|3 = Arbeitsmethode}} | |||
=14.02.2025: Dividieren von Dezimalbrüchen und Hausaufgabe zum Multiplizieren von Dezimalbrüchen= | |||
{{Box |1= Zur Wiederholung und Erinnerung an die 5. Klasse: |2= Berechne <math> 5472 \div 12 </math> schriftlich! | |||
{{Lösung versteckt|1= <math> 5472 \div 12 = 456 </math> |2= Aufdecken|3=Verbergen}} | |||
|3= Arbeitsmethode}} | |||
{{Box|1= Neu: |2= Heute geht es los mit dem '''Dividieren von Dezimalbrüchen''', zunächst mit dem '''Dividieren von Dezimalbrüchen durch eine natürliche Zahl'''. Bevor du mit dem Video startest, notiere dir bitte die beiden fett gedruckten Sätze als Überschrift in dein Heft! <br> Sieh dir nun zunächst folgendes Video aufmerksam an! Notiere dir zeitgleich die drei Aufgaben, die im Video berechnet werden auf einem Schmierzettel, damit du diese im Anschluss an das Video noch einmal alleine berechnen kannst...| 3= Arbeitsmethode}} | |||
{{Box| FÜR DIE WIEDERHOLUNG ZU HAUSE: Dividieren von Dezimalbrüchen: |{{#ev:youtube|4IosoF-ldMs}} | Hervorhebung1}} | |||
{{Box |1= Zum Einstieg: |2= Wir berechnen gemeinsam ein paar Beispiele. Zu Hause kannst du die Vorgehensweise beim "Dividieren von Dezimalbrüchen durch eine natürliche Zahl" nochmals mit dem Video von Lehrer Schmidt vertiefen; unsere Einstiegsbeispiele sollten dir bereits bekannt vorkommen ;-) | |||
{{Lösung versteckt|1= <math> 25,8 \div 6 = 4,3 </math> <br> <math> 0,049 \div 7 = 0,007 </math> <br> <math> 37,65 \div 12 = 3,1375 </math> |2= Aufdecken|3=Verbergen}} | |||
|3= Üben}} | |||
{{Box|1= Und alles klar? |2= Notiere bitte folgenden Merksatz in dein Heft! <br> | |||
<u>'''Merke: Division eines Dezimalbruchs durch eine natürliche Zahl'''</u> <br> | |||
# Dividiere den Dezimalbruch stellenweise durch die natürliche Zahl, so wie du es von der Division einer natürlichen Zahl durch eine natürliche Zahl bereits gewohnt bist. | |||
# Wichtig: Sobald du bei der Berechnung das Komma "überschreitest", setze auch im Ergebnis ein Komma! | |||
# Eventuell ist es nötig, um die Aufgabe komplett berechnen zu können, zum Ende des Rechenvorgangs beim Dezimalbruch noch nicht geschriebene Endnullen zu ergänzen. | |||
<br> Lies dir diesen Merksatz nun noch einmal in Ruhe durch und verinnerliche die Vorgehensweise bei der Division eines Dezimalbruchs durch eine natürliche Zahl bevor es mit Übungen weiter geht! | |||
|3= Merksatz}} | |||
{{Box |1= Zur Übung: |2= Kopfrechnen - Schlage das Buch S. 110/ 2 auf, stelle dir einen Timer auf 5 Minuten und versuche in der Zeit so viele Aufgaben wie möglich zu berechnen. <br> Notiere dir jeweils dein Ergebnis, damit du deine Lösung mit meiner im Anschluss vergleichen kannst.... Ich hoffe du bist schon zurecht gekommen! | |||
{{Lösung versteckt|1= a) 0,7; b) 0,8; c) 0,8; d) 1,8; e) 2,4; f) 3,25; g) 0,16; h) 0,04; i) 1,2; j) 1,2; k) 0,22; l) 0,17; |2= Aufdecken|3=Verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Zur Übung: |2= Nun bestimmt etwas schwieriger für dich: Berechne B. S. 110/ 5 a), b), c), d), g) und freiwillig e)! <br> Versuche konzentriert jede Aufgabe zu berechnen, wende dein neu erworbenes Wissen an und versuche ruhig zu bleiben, dann kommst du sicher ans Ziel! <br> Mit diesen Aufgaben sollst du Rechenroutine bekommen... Bitte bei Teilaufgabe e), falls du diese freiwillig versuchst, nach spätestens 5 Minuten aufhören! <br> Verbessere bitte deinen Lösungsvorschlag! <br> Falls dein Ergebnis ein anderes sein sollte, dann vergleiche bitte deine Lösung Schritt für Schritt mit der von mir! | |||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag B S 110 5 a b c d e g.jpg]] |2= Lösung Aufgabe 5 anzeigen | 3= Lösung verbergen}} | |||
|3= Üben}} | |||
{{Box |1= HAUSAUFGABE - Zur Wiederholung und Vertiefung: |2= Damit du das Multiplizieren von Dezimalbrüchen nicht so schnell vergisst, wirst du es mit folgenden Aufgaben zum einen wiederholen und zum anderen weiter vertiefen. <br> Parat haben solltest du hierfür auch das Wissen zu Potenzen und die Rechenvorschrift "von links nach rechts"... <br> Berechne nun Buch S. 107/ 20 a), b), c) und S. 107/ 22 e), f)! | |||
{{Lösung versteckt|1= | |||
'''Tipp:''' Berechne hier Schritt für Schritt von "links nach rechts"! Vergiss die Zwischenschritte nicht! <br> | |||
a) 1,4·2,6·3 = 3,64·3 = 10,92 | |||
b) 4,9·7·1,5 = 34,3·1,5 = 51,45 | |||
c) 0,62·0,25·17,8 = 0,155·17,8 = 2,759 | |||
|2= B. S. 107/ 20 a), b), c) Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1= | |||
e) 1,2<sup>3</sup> = 1,2·1,2·1,2 = 1,44·1,2 = 1,728 | |||
f) 2,5<sup>3</sup> = 2,5·2,5·2,5 = 6,25·2,5 = 15,625 | |||
|2= B. S. 107/ 22 e), f) Aufdecken|3=Verbergen}} | |||
|3=Lösung}} | |||
=18.02.2025: Hausaufgabe = | |||
{{Box|1=Hausaufgabe|2= WICHTIG: Vergiss nicht die Lösung der Aufgabenpaare im Schulheft zu berechnen/ zu notieren, nachdem du diese zugeordnet hast! <br> | |||
{{LearningApp|app=peoyd3ns321|width=100%|height=600px}} | |||
{{Lösung versteckt|1= Die Aufgabenpaare inklusive zugehöriger Lösung: | |||
*32 : 800 = 0,32 : 8 = 0,04 | |||
*32 : 8 = 3,2 : 0,8 = 4 | |||
*3200 : 8 = 32 : 0,08 = 400 | |||
*30 : 6 = 0,3 : 0,06 = 5 | |||
*300: 6 = 3 : 0,06 = 50 | |||
*96 : 12 = 0,96 : 0,12 = 8 <br> | |||
Die links notierte Rechenaufgabe ist die, die man einfacher berechnen kann. | |||
|2=Aufdecken|3=Verbergen}} | |||
|3=Üben}} | |||
{{Box |1= Ausblick: |2= Du hast es dir sicher schon gedacht, auch beim Rechnen mit Dezimalzahlen gelten nach wie vor die Rechenregeln "Klammern zuerst", "Potenz vor Punkt vor Strich", "von links nach rechts" und natürlich können Dezimalbrüche auch in Textaufgaben vorkommen...<br> Berechne die jeweilige Aufgabe im Kopf! Mit diesen Aufgaben kannst du testen, ob du Rechengesetze richtig anwendest und Textaufgaben richtig verstehst... Wenn du magst, kannst du dir hierbei freiwillig die jeweilige Aufgabe inklusive ihrer Lösung kurz ins Schulheft notieren. <br> Anmerkung: Pickerl = Sticker <br> {{LearningApp|app=2051792|width=100%|height=700px}} | |||
|3= Arbeitsmethode}} | |||
{{Box |1= Zum Abschluss: |2= Noch etwas Kopfrechnen - Schlage das Buch S. 114/ 4 auf und berechne nacheinander die Aufgaben im Kopf. <br> Notiere dir jeweils dein Ergebnis, damit du deine Lösung mit meiner im Anschluss vergleichen kannst.... | |||
{{Lösung versteckt|1= a) "32 : 8" = 4; b) "56 : 7" = 8; c) "30 : 6" = 5; d) "40 : 5" = 8; <br> e) "50 : 25" = 2; f) "2000 : 2" = 1000; g) "15 : 3" = 5; h) "30 : 6" = 5; <br> i) "200 : 4" = 50; j) "64: 8" = 8; k) "250 : 2" = 125; l) "1800 : 6" = 300; |2= Aufdecken|3=Verbergen}} | |||
|3= Üben}} | |||
{{Box |1= '''FREIWILLIG''' - Zur Vertiefung: |2= Potenzen und Dezimalbrüche...<br> Berechne jeweils und ordne das richtige Ergebnis zu. Achte hierbei auf die richtige Anzahl der Nachkommastellen! <br> {{LearningApp|app=8763352|width=100%|height=700px}} | |||
|3= Arbeitsmethode}} | |||
=10.03.2025: Hausaufgabe - Zur Wiederholung = | |||
{{Box |1= Wiederholung: |2= Fasse mündlich noch einmal für dich zusammen, was ein endlicher Dezimalbruch ist und wie er entsteht! <br> Definiere, was ein periodischer Dezimalbruch ist, wie ist hierbei die Notation! <br> Lerne den Zusammenhang zwischen Brüchen mit Nenner 9 und ihren periodischen Dezimalbrüchen! <br> | |||
|3= Üben}} | |||
{{Box |1= LERNE!! - Brüche mit Nenner 9: |2= Bitte keine Panik, das ist nicht so viel, wie es auf den ersten Blick wirkt, du erkennst sicherlich ein Schema beim Lernen und denke bitte immer an die Möglichkeit des '''Kürzens''', das erklärt doch auch so einiges... | |||
{{Lösung versteckt |1= Merke dir: <br> | |||
*<math> {1 \over 9} = 0,\bar{1}</math>; ''"null Komma Periode eins"'' <br> | |||
*<math> {2 \over 9} = 0,\bar{2}</math>; ''"null Komma Periode zwei"'' <br> | |||
*<math> {3 \over 9} = {1 \over 3} = 0,\overline{3}</math>; ''"null Komma Periode drei"'' <br> | |||
*<math> {4 \over 9} = 0,\bar{4}</math>; ''"null Komma Periode vier"'' <br> | |||
*<math> {5 \over 9} = 0,\bar{5}</math>; ''"null Komma Periode fünf"'' <br> | |||
*<math> {6 \over 9} = {2 \over 3} = 0,\overline{6}</math>; ''"null Komma Periode sechs"'' <br> | |||
*<math> {7 \over 9} = 0,\bar{7}</math>; ''"null Komma Periode sieben"'' <br> | |||
*<math> {8 \over 9 }= 0,\bar{8}</math>; ''"null Komma Periode acht"'' <br> | |||
*<math> {9 \over 9} = 0,\bar{9} = 1 </math> <br> | |||
|2= Merke anzeigen | 3= Merke verbergen}} | |||
|3= Merksatz}} | |||
{{Box |1= Test:|2= Zum Überprüfen und weiteren Vertiefen deines gelernten Wissens kannst du hier '''freiwillig''' noch einmal Paare von Brüchen und Dezimalbrüchen passend zuordnen. Mit der folgenden LearningApp hast du die Möglichkeit zu testen, ob du besondere Brüche und ihre zugehörigen Dezimalzahlen bereits gut genug gelernt hast. Viel Freude dabei! <br> {{LearningApp|app=ppjjvkti321|width=100%|height=700px}} | |||
|3= Arbeitsmethode}} | |||
{{Box |1= Test: |2= Zur Wiederholung und Vertiefung: Endlich oder unendlicher Bruch? Sortiere jeweils zu! Kürzen bzw. Erweitern auf 10, 100, 1000, 10000, ... kann dir dabei helfen endliche Brüche "herauszuangeln..." <br> {{LearningApp|app=8373214|width=100%|height=700px}} | |||
|3= Arbeitsmethode}} | |||
=25.03.2025: Hausaufgabe zu Parallelogramm und Wiederholung zu Einheiten = | |||
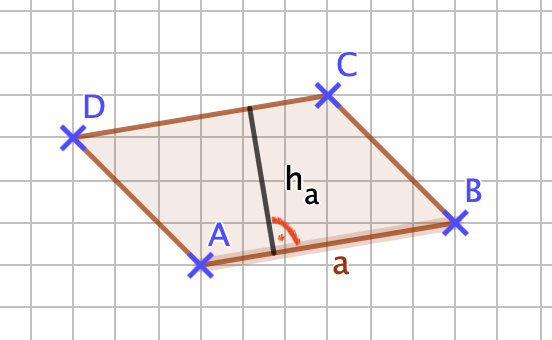
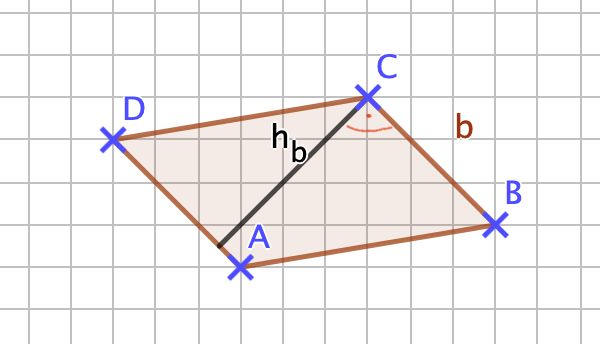
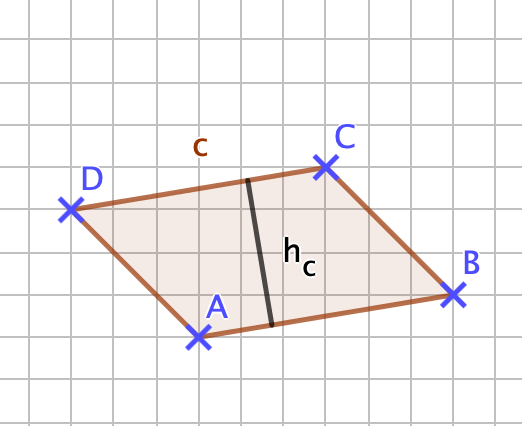
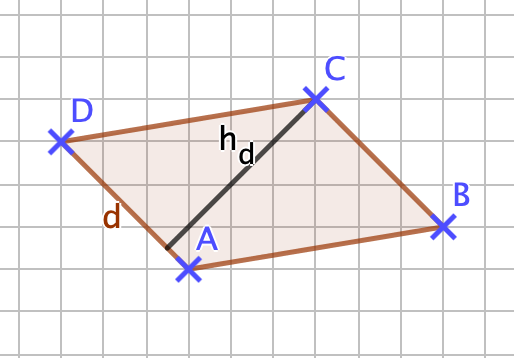
{{Box |1= Erinnerung: |2= Zur Berechnung des Flächeninhalts eines Parallelogramms benötigt man, wie du weißt, die Höhen im Parallelogramm. Mit folgender Darstellung kannst du erkennen, wie die Höhe im Parallelogramm dargestellt wird. Verschiebe die blauen Punkte des Parallelogramms mit deiner Maus und beobachte dabei, wann sich die Höhen innerhalb bzw. außerhalb des Parallelogramms befinden und wie man diese einzeichnet. <br> | |||
<ggb_applet id="BkjVfyDh" width="800" height="600" /> | |||
<br> | |||
<br> | |||
|3= Unterrichtsidee}} | |||
{{Box|Hinweis:| | |||
{{Lösung versteckt|1= | |||
'''Höhen im Parallelogramm'''<br> | |||
Unter den Höhen eines Parallelogramms versteht man die Abstände der zueinander parallelen Seiten des Parallelogramms. Ein Parallelogramm hat zwei Höhen. <br> | |||
Man zeichnet die Höhe, indem man eine Strecke rechtwinklig zu einer Seite zeichnest und diese mit der dazu parallelen Seite verbindest. | |||
<br> | |||
|2=Aufdecken|3=Verbergen}} | |||
|3=Merksatz}} | |||
{{Box| FREIWILLIG - Einzeichnen der Höhen - 1: |{{#ev:youtube|WULo-g3PBPQ}} | Hervorhebung1}} | |||
{{Box| FREIWILLIG - Einzeichnen der Höhen - 2: |{{#ev:youtube|jRXu-vDyK3k}} | Hervorhebung1}} | |||
{{Box |1= Übung - Berechnung des Flächeninhalts von Parallelogrammen:|2= Nun darfst du selbst die Höhe suchen.... und hoffentlich finden! Falls das noch nicht so gut klappen sollte, nochmal der Hinweis auf die freiwilligen Videos vorab zum Zeichnen der Höhen beim Parallelogramm. <br> {{LearningApp|app=pgc0vz74j19|width=100%|height=600px}} | |||
|3= Arbeitsmethode}} | |||
{{Box |1= Zur Wiederholung:|2= Zum Abschluss der heutigen Hausaufgabe noch etwas Umrechnen von Einheiten - zunächst Längeneinheiten... Du musst hier nicht alle Aufgaben bearbeiten, sollten dir die einfachen zu einfach sein, dann lass sie bitte einfach weg, die zu "schwieriger" sind jedoch Pflicht! <br> | |||
Zum Reinkommen in das Umrechnen von Einheiten können die "einfachen" Aufgaben aber auch hilfreich sein, dies entscheidest du aber vollkommen selbstständig, je nachdem, wie gut du dich noch an das Umrechnen von Einheiten erinnern kannst!<br> {{LearningApp|app=11240926|width=100%|height=700px}} <br>|3= Arbeitsmethode}} | |||
{{Box |1= Zur Wiederholung:|2= Und nun noch etwas Umrechnen von Einheiten - ein paar Flächeneinheiten... <br> {{LearningApp|app=pfhyzuzvn21|width=100%|height=700px}} <br> |3= Arbeitsmethode}} | |||
=28.03.2025: Hausaufgabe = | |||
{{Box |1= Übung: |2= Bevor du startest wiederhole bitte für dich die Formel zur Berechnung des Flächeninhalts eines Parallelogramms und auch die Formel zur Berechnung seines Umfangs. <br> | |||
Bearbeite bitte im Buch S. 141/ 6! <br> | |||
Berechne Zeile für Zeile und verbessere immer direkt im Anschluss deine Lösung mit dem folgenden Lösungsvorschlag. <br> Lass dich nicht irritieren, du fertigst im Heft nur eine Skizze des Parallelogramms an - hier ist für jede Zeile eine Skizze angefügt, dies dient der besseren Übersichtlichkeit und Nachvollziehbarkeit der Lösung. | |||
{{Lösung versteckt|1=[[Datei:141-6-1.png]]<br>Wenn du richtig gezeichnet hast, dann müsste die Seite <math>\overline{AB} = a </math> ca. 3cm sein und die zugehörige Höhe ca. 1,7cm. <br> Der Flächeninhalt ist dann: A=3cm•1,7cm=5,1cm² <br> | |||
Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 1 Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:141-6-2.png]]<br>Die Länge der Seite <math> \overline{BC} = b </math> ist ca. 2,1cm die zugehörige Höhe ist ca. 2,5cm. <br> Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 2 Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:141-6-4.png]]<br>Die Länge der Seite <math> \overline{CD} = c </math> ist ca. 3cm, c =a! Die zugehörige Höhe ist dann ebenfalls, wie auch die Höhe zur Seite a, ca. 1,7cm. <br> Mit diesen Werten kommt man auf einen Flächeninhalt von 5,1cm². |2=Zeile 3 Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:141-6-3.png]]<br>Die Länge der Seite <math> \overline{DA} = d </math> ist ca. 2,1cm, d = b! Die zugehörige Höhe ist, wie auch die Höhe zur Seite b, ca. 2,5cm. Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². <br> | |||
'''Feststellung und Begründung:''' | |||
Unterschiede im Flächeninhalt entstehen aufgrund von Messungenauigkeiten. Eigentlich sollte bei jeder Messung und Rechnung immer der gleiche Flächeninhalt herauskommen, die Fläche des Parallelogramms verändert sich ja nicht.... |2=Zeile 4 Aufdecken|3=Verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Übung: |2= Bearbeite B. S. 142/ 12 b), c)! <br> Vergiss nicht die Anwendungsmöglichkeit einer Umkehrrechnung... | |||
{{Lösung versteckt |1= '''Lösung der Aufgaben:''' <br> | |||
'''b)''' <br> | |||
h = 5,2 cm und A = 22,36 cm² <br> Löse mit der Umkehraufgabe: <br> | |||
<math> g= A \div h = 22,36 cm^2 \div 5,2 cm = 223,6 cm^2 \div 52 cm = 4,3 cm </math> <br> Vergiss bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! | |||
'''c)''' <br> | |||
Am besten du rechnest beide Größen sofort in dieselbe Einheit um! <br> g = 150 cm und A = 9,75 m² = 975 dm² = 97500 cm² <br> Löse mit der Umkehraufgabe: <br> | |||
<math> h= A \div g = 97500 cm^2 \div 150 cm = 650 cm = 6,5 m </math> <br> Vergiss auch hier bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! | |||
|2= Lösung anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |3= Üben}} | ||
Version vom 25. März 2025, 16:18 Uhr
31.01.2025: Übungen zu Multiplizieren mit Stufenzahlen und Dividieren durch Stufenzahlen
Zur Vorbereitung zu Hause auf die kommende Stunde - Multiplizieren von Dezimalbrüchen
03.02.25: Weiter geht es mit dem Multiplizieren von Dezimalbrüchen
14.02.2025: Dividieren von Dezimalbrüchen und Hausaufgabe zum Multiplizieren von Dezimalbrüchen
18.02.2025: Hausaufgabe
10.03.2025: Hausaufgabe - Zur Wiederholung
25.03.2025: Hausaufgabe zu Parallelogramm und Wiederholung zu Einheiten