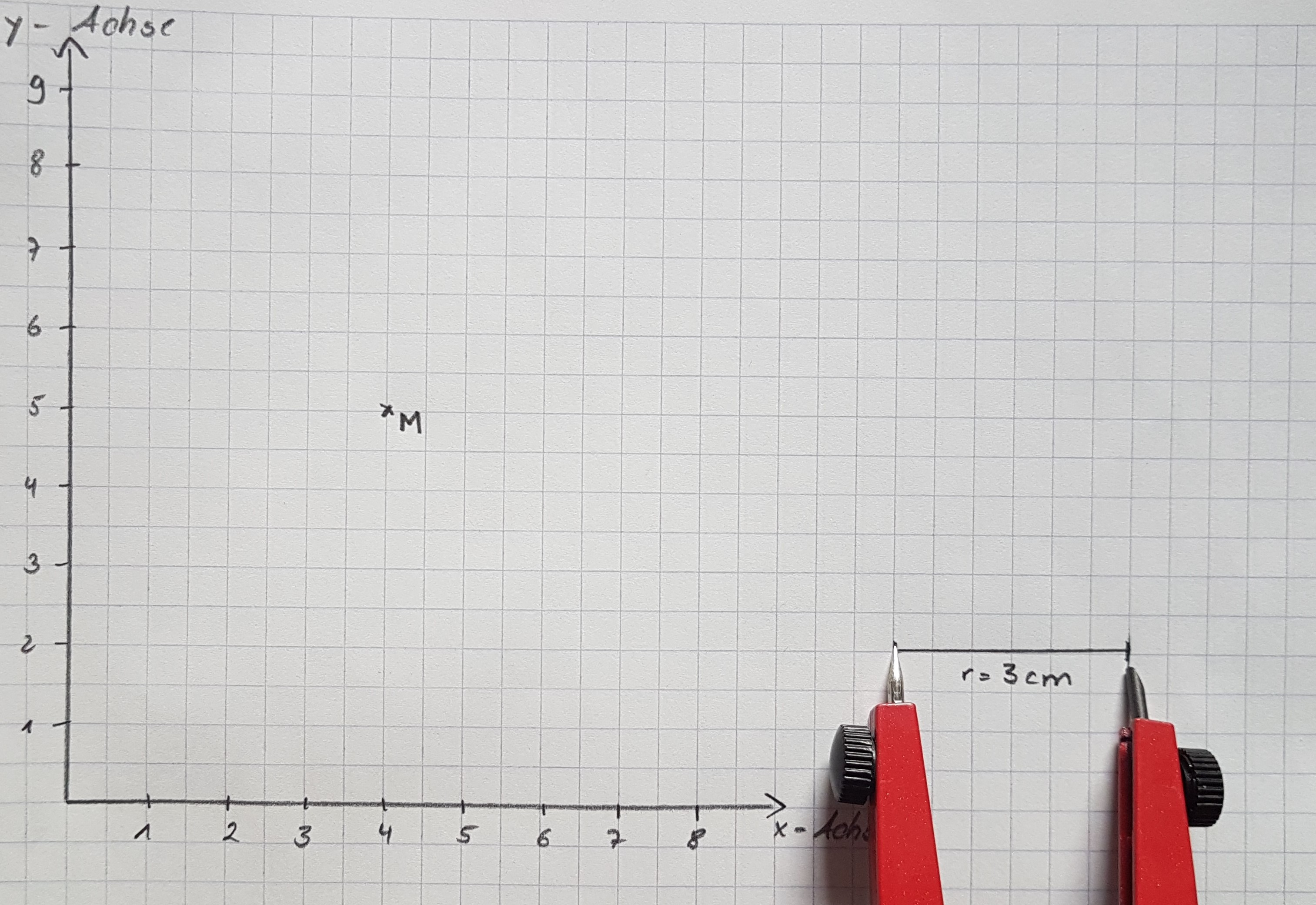Kreis: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 24: | Zeile 24: | ||
Das üben wir jetzt kurz im Übungsheft: | Das üben wir jetzt kurz im Übungsheft: | ||
<div class="grid"> | |||
<div class="width-2-3"> | |||
Zeichne den Kreis k(M;3) mit dem Mittelpunkt M(4/5). | Zeichne den Kreis k(M;3) mit dem Mittelpunkt M(4/5). | ||
| Zeile 32: | Zeile 32: | ||
#Stellt auf eurem Zirkel 3 cm ein. | #Stellt auf eurem Zirkel 3 cm ein. | ||
#Stecht in den Mittelpunkt M ein und zeichnet den Kreis von 3 cm. | #Stecht in den Mittelpunkt M ein und zeichnet den Kreis von 3 cm. | ||
</div> | |||
<div class="width-2-3"> | |||
[[Datei:M5 III 06 Kreise 01.jpg|midi]] | [[Datei:M5 III 06 Kreise 01.jpg|midi]] | ||
[[Datei:M5 III 06 Kreise Radius nehmen.jpg|links|midi]] | [[Datei:M5 III 06 Kreise Radius nehmen.jpg|links|midi]] | ||
</div> | |||
</div> | |||
Version vom 26. März 2020, 09:05 Uhr
Die Begriffe Radius und Durchmesser kennt ihr aus der Grundschule und dazu habt ihr einen Eintrag in euer Merkheft geklebt.
Jetzt kommt eine neue Schreibweise:
Damit man nicht schreiben muss: Der Kreis k mit Mittelpunkt M und Radius r.
Schreiben wir dafür kurz: k(M;r)
Notiere in dein Merkheft:
Das üben wir jetzt kurz im Übungsheft:
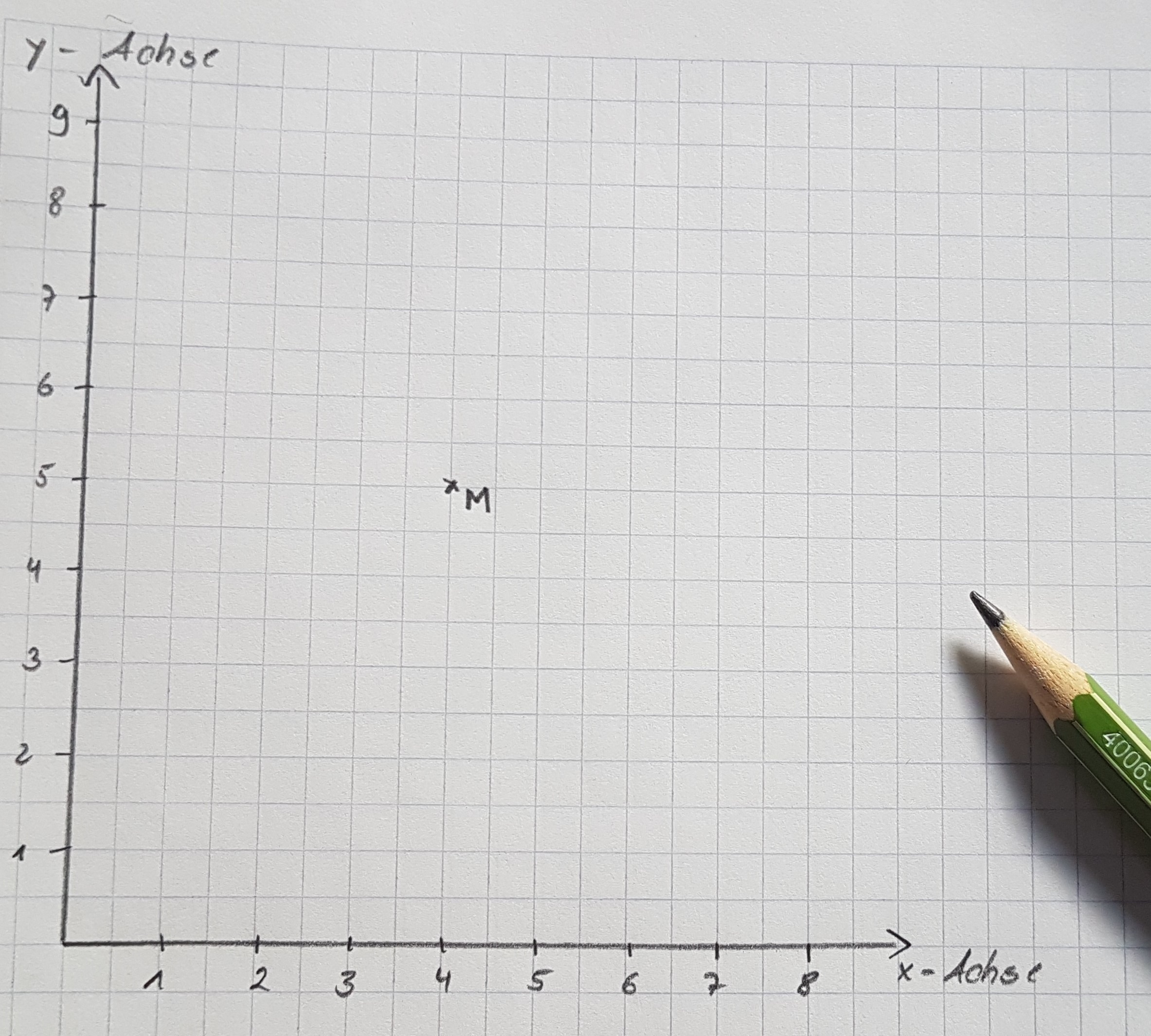
Zeichne den Kreis k(M;3) mit dem Mittelpunkt M(4/5).
- Zeichne ein Koordinatensystem bei der ihr pro Achse 8 Einheiten (cm benötigt).
- Markiert den Mittelpunkt M(4/5).
- Stellt auf eurem Zirkel 3 cm ein.
- Stecht in den Mittelpunkt M ein und zeichnet den Kreis von 3 cm.
So sieht das dann aus ...
Sieht auch dein Kreis so aus, dann zeichne ihn auch in dein Merkheft und schreibe „k(M;3) mit dem Mittelpunkt M(4|5)“ daneben
Nun zeichnet in das gleiche Koordinatensystem den Kreis k(M;4) und k(M;2) mit dem gleichen Mittelpunkt wie eben.
Und weil es so viel Spaß macht!
Zeichnet ein neues Koordinatensystem mit folgenden Kreisen:
a) k(M; 3) mit M(8|7)
b) k(M; 3) mit M(3|4)
c) k(M; 2) mit M(8|4)
Das hast du super gemacht!!!