6e Lernen zu Hause: Brüche und Dezimalbrüche: Unterschied zwischen den Versionen
Aus RMG-Wiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 399: | Zeile 399: | ||
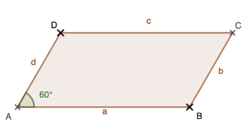
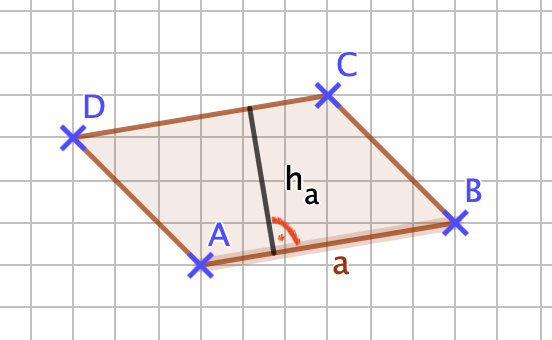
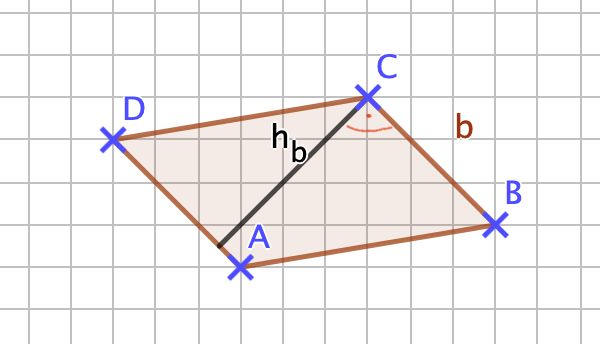
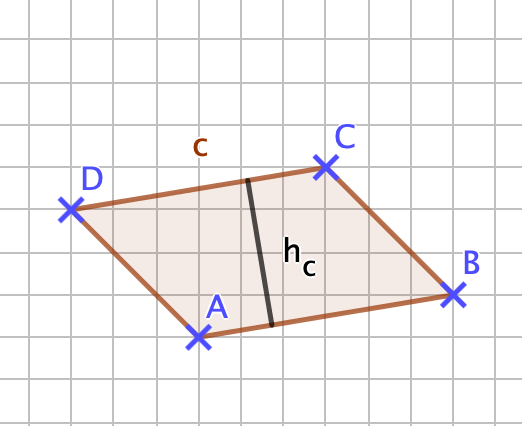
{{Box|1= Idee: |2= Herleitung der Formel zur Berechnung des '''Flächeninhalts A eines Dreiecks'''. <br> | {{Box|1= Idee: |2= Herleitung der Formel zur Berechnung des '''Flächeninhalts A eines Dreiecks'''. <br> | ||
Um den Flächeninhalt eines Dreiecks bestimmen zu können, erinnert man sich zunächst an die Berechnung des Flächeninhalts eines Rechtecks <math>A= a \cdot b</math>, a beschreibt die Länge und b die Breite des Rechtecks. <br> Vielleicht hast du auch schon eine Idee, wie man den Flächeninhalt eines Dreiecks mit dem Wissen zur Berechnung des Flächeninhalts eines Rechtecks bestimmen kann? <br> Bevor du dir den entsprechenden Merksatz in dein Heft notieren wirst, schau dir im Folgenden Schritt für Schritt eine der Möglichkeiten an, wie der Flächeninhalt eines Dreiecks bestimmt werden kann. <br> Am Montag wirst du noch eine andere Idee kennen lernen, aber das Ergebnis ist dasselbe wie heute, die Formel zur Berechnung des Flächeninhalts eines Dreiecks bleibt gleich... <br> Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite - z.B. indem du F5 drückst, dann sollte es normalerweise klappen... | Um den Flächeninhalt eines Dreiecks bestimmen zu können, erinnert man sich zunächst an die Berechnung des Flächeninhalts eines Rechtecks <math>A= a \cdot b</math>, a beschreibt die Länge und b die Breite des Rechtecks. <br> Vielleicht hast du auch schon eine Idee, wie man den Flächeninhalt eines Dreiecks mit dem Wissen zur Berechnung des Flächeninhalts eines Rechtecks bestimmen kann? <br> Bevor du dir den entsprechenden Merksatz in dein Heft notieren wirst, schau dir im Folgenden Schritt für Schritt eine der Möglichkeiten an, wie der Flächeninhalt eines Dreiecks bestimmt werden kann. <br> Am Montag wirst du noch eine andere Idee kennen lernen, aber das Ergebnis ist dasselbe wie heute, die Formel zur Berechnung des Flächeninhalts eines Dreiecks bleibt gleich... <br> Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite - z.B. indem du "F5" auf der Tastatur drückst, dann sollte es normalerweise klappen... | ||
<ggb_applet id="tT6Yj7Dg" width="800" height="450" border="888888" /> | <ggb_applet id="tT6Yj7Dg" width="800" height="450" border="888888" /> | ||
| Zeile 447: | Zeile 447: | ||
g = 9 cm und h = 4 cm <br> | g = 9 cm und h = 4 cm <br> | ||
<math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 9 cm \cdot 4 cm = \frac{1}{2} \cdot (9 cm \cdot 4 cm) = \frac {1}{2} 36 cm^2 = 18 cm^2 </math> <br> | <math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 9 cm \cdot 4 cm = \frac{1}{2} \cdot (9 cm \cdot 4 cm) = \frac {1}{2} \cdot 36 cm^2 = 18 cm^2 </math> <br> | ||
'''b)''' <br> | '''b)''' <br> | ||
g = 6 cm und h = 4 cm oder aber auch g = 4 cm und h = 6 cm, denn zwei Seiten des Dreiecks stehen aufeinander senkrecht. Damit ist die eine Seite die Höhe zu der Seite, auf der sie senkrecht steht oder eben umgekehrt...<br> | g = 6 cm und h = 4 cm oder aber auch g = 4 cm und h = 6 cm, denn zwei Seiten des Dreiecks stehen aufeinander senkrecht. Damit ist die eine Seite die Höhe zu der Seite, auf der sie senkrecht steht oder eben umgekehrt...<br> | ||
<math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 6 cm \cdot 4 cm = \frac{1}{2} \cdot (6 cm \cdot 4 cm) = \frac {1}{2} 24 cm^2 = 12 cm^2 </math> <br> | <math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 6 cm \cdot 4 cm = \frac{1}{2} \cdot (6 cm \cdot 4 cm) = \frac {1}{2} \cdot 24 cm^2 = 12 cm^2 </math> <br> | ||
'''d)''' <br> | '''d)''' <br> | ||
ACHTUNG: g = 3,5 cm und h = 2,7 cm <br> | ACHTUNG: g = 3,5 cm und h = 2,7 cm <br> | ||
<math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 3,5 cm \cdot 2,7 cm = \frac{1}{2} \cdot (3,5 cm \cdot 2,7 cm) = \frac {1}{2} 9,45 cm^2 = 9,45 cm^2 \div 2= 4,725 cm^2 </math> <br> Anmerkung: "<math> \frac{1}{2} \cdot </math>" entspricht "geteilt durch 2", was manchmal leichter im Kopf zu berechnen ist.... Man bestimmt ja letztendlich die Hälfte...<br> | <math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 3,5 cm \cdot 2,7 cm = \frac{1}{2} \cdot (3,5 cm \cdot 2,7 cm) = \frac {1}{2} \cdot 9,45 cm^2 = 9,45 cm^2 \div 2= 4,725 cm^2 </math> <br> Anmerkung: "<math> \frac{1}{2} \cdot </math>" entspricht "geteilt durch 2", was manchmal leichter im Kopf zu berechnen ist.... Man bestimmt ja letztendlich die Hälfte...<br> | ||
|2= Lösung der Aufgabe anzeigen | 3= Lösung verbergen}} <br> | |2= Lösung der Aufgabe anzeigen | 3= Lösung verbergen}} <br> | ||
|3= Üben}} | |3= Üben}} | ||
Aktuelle Version vom 27. Februar 2021, 19:05 Uhr
15.02.2021
17.02.2021
18.02.2021
22.02.2021
24.02.2021
25.02.2021