6e Lernen zu Hause: Brüche und Dezimalbrüche: Unterschied zwischen den Versionen
Aus RMG-Wiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (48 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 282: | Zeile 282: | ||
==24.02.2021== | ==24.02.2021== | ||
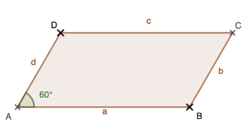
{{Box |1= Übung: |2= Bevor du startest | {{Box |1= Übung: |2= Bevor du startest wiederhole bitte für dich die Formel zur Berechnung des Flächeninhalts eines Parallelogramms und auch die Formel zur Berechnung seines Umfangs. Solltest du feststellen, dass noch etwas unklar ist, dann schau dir bitte entsprechend das Erklärvideo der vergangenen Stunde an. Danke! <br> Wenn alles klar ist, dann geht's auch schon los.... <br> | ||
{{Lösung versteckt|1=[[Datei:141-6-1.png]]<br>Wenn du richtig gezeichnet hast, dann müsste die Seite <math>\ | Bearbeite bitte im Buch S. 141/ 6! <br> | ||
Berechne Zeile für Zeile und verbessere immer direkt im Anschluss deine Lösung mit dem folgenden Lösungsvorschlag. <br> Lass dich nicht irritieren, du fertigst im Heft nur eine Skizze des Parallelogramms an - hier ist für jede Zeile eine Skizze angefügt, dies dient der besseren Übersichtlichkeit und Nachvollziehbarkeit der Lösung. | |||
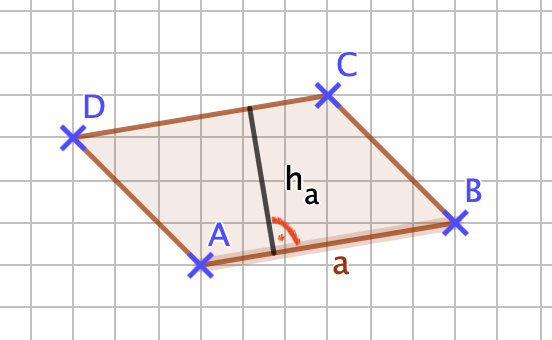
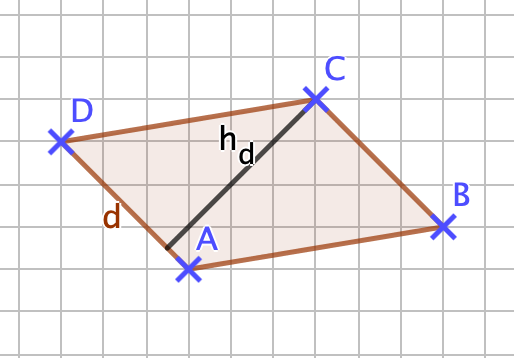
{{Lösung versteckt|1=[[Datei:141-6-1.png]]<br>Wenn du richtig gezeichnet hast, dann müsste die Seite <math>\overline{AB} = a </math> ca. 3cm sein und die zugehörige Höhe ca. 1,7cm. <br> Der Flächeninhalt ist dann: A=3cm•1,7cm=5,1cm² <br> | |||
Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 1 Aufdecken|3=Verbergen}} | Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 1 Aufdecken|3=Verbergen}} | ||
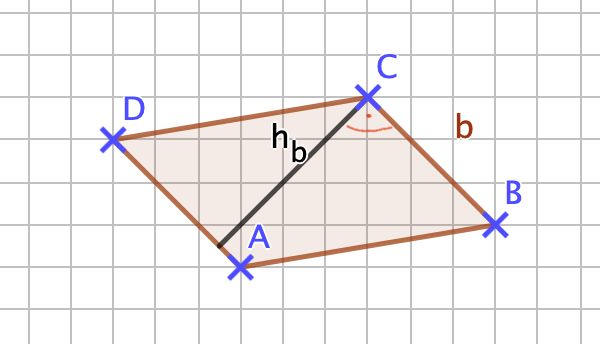
{{Lösung versteckt|1=[[Datei:141-6-2.png]]<br>Die Länge der Seite b ist ca. 2,1cm die zugehörige Höhe ist ca. 2,5cm. Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 2 Aufdecken|3=Verbergen}} | {{Lösung versteckt|1=[[Datei:141-6-2.png]]<br>Die Länge der Seite <math> \overline{BC} = b </math> ist ca. 2,1cm die zugehörige Höhe ist ca. 2,5cm. <br> Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². Sollten deine Werte um 1-2mm abweichen ist das kein Problem. |2=Zeile 2 Aufdecken|3=Verbergen}} | ||
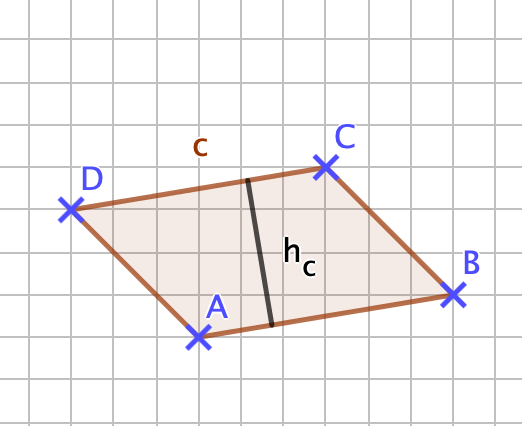
{{Lösung versteckt|1=[[Datei:141-6-4.png]]<br>Die Länge der Seite <math> \overline{CD} = c </math> ist ca. 3cm, c =a! Die zugehörige Höhe ist dann ebenfalls, wie auch die Höhe zur Seite a, ca. 1,7cm. <br> Mit diesen Werten kommt man auf einen Flächeninhalt von 5,1cm². |2=Zeile 3 Aufdecken|3=Verbergen}} | |||
{{Lösung versteckt|1=[[Datei:141-6-3.png]]<br>Die Länge der Seite <math> \overline{DA} = d </math> ist ca. 2,1cm, d = b! Die zugehörige Höhe ist, wie auch die Höhe zur Seite b, ca. 2,5cm. Mit diesen Werten kommt man auf einen Flächeninhalt von 5,25cm². <br> | |||
'''Feststellung und Begründung:''' | |||
Unterschiede im Flächeninhalt entstehen aufgrund von Messungenauigkeiten. Eigentlich sollte bei jeder Messung und Rechnung immer der gleiche Flächeninhalt herauskommen, die Fläche des Parallelogramms verändert sich ja nicht.... |2=Zeile 4 Aufdecken|3=Verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Übung: |2= Bearbeite B. S. 142/ 12 a), b), c)! <br> Vergiss nicht die Anwendungsmöglichkeit einer Umkehrrechnung... | |||
{{Lösung versteckt |1= '''Lösung der Aufgaben:''' <br> | |||
'''a)''' <br> | |||
g = 16,2 cm und h = 3,5 cm <br> | |||
<math> A = g \cdot h = 16,2 cm \cdot 3,5 cm = 56,7 cm^2 </math> <br> | |||
'''NR:''' <math> 162\cdot 35 = 5670 </math>, da die beiden Faktoren zusammen zwei Nachkommastellen haben, ist das Ergebnis für den Flächeninhalt 56,7(0) cm². Vergiss bitte nicht "<math> cm \cdot cm = cm^2 </math>"! | |||
'''b)''' <br> | |||
h = 5,2 cm und A = 22,36 cm² <br> Löse mit der Umkehraufgabe: <br> | |||
<math> g= A \div h = 22,36 cm^2 \div 5,2 cm = 223,6 cm^2 \div 52 cm = 4,3 cm </math> <br> Vergiss bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! | |||
'''c)''' <br> | |||
Am besten du rechnest beide Größen sofort in dieselbe Einheit um! <br> g = 150 cm und A = 9,75 m² = 975 dm² = 97500 cm² <br> Löse mit der Umkehraufgabe: <br> | |||
<math> h= A \div g = 97500 cm^2 \div 150 cm = 650 cm = 6,5 m </math> <br> Vergiss auch hier bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! | |||
|2= Lösung anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box |1= Übung: |2= Bearbeite B. S. 142/ 16! <br> Vergiss auch hier nicht die Anwendungsmöglichkeit einer Umkehrrechnung... Falls du überhaupt keine Idee hast, wie du bei dieser Aufgabe starten sollst, schau dir den 1. Tipp an! | |||
{{Lösung versteckt |1= '''1. Tipp:''' <br> | |||
Berechne zuerst den Flächeninhalt A! Sowohl a als auch h<sub>a</sub> sind gegeben! <br> | |||
Falls du nicht weiterkommen solltest, schau dir den 2. Tipp an! | |||
|2= 1. Tipp anzeigen | 3= 1. Tipp verbergen}} <br> | |||
{{Lösung versteckt |1= '''2. Tipp:''' <br> | |||
Zur Kontrolle A = 14,25 cm². <br> | |||
Bei der Aufgabe ist auch die Seite b gegeben, den Flächeninhalt des Parallelogramms hätte man auch aus dem Produkt der Seite b und ihrer zugehörigen Höhe h<sub>b</sub> berechnen können... <br> | |||
Wenn dir das klar ist, dann kannst du auch unter Verwendung einer Umkehraufgabe die Höhe h<sub>b</sub> aus der Flächenformel <math> A = b \cdot h_b </math> heraus berechnen. <br> | |||
Ich hoffe sehr, dass dich die Tipps weiter ans Ziel gebracht haben! Falls dem nicht so ist, schau dir bitte die Lösung von mir Schritt für Schritt an und versuche diese zu verstehen. Falls dies auch nicht helfen sollte, kannst du morgen in der 5. Stunde in einer "Videosprechstunde" nochmal bei mir nachfragen. Vielleicht bis morgen...<br> | |||
'''Anmerkung:''' Bitte wundere dich nicht über das "krumme" Ergebnis für die Höhe h<sub>b</sub>, das ist auf den ersten Blick komisch, soll aber so sein... | |||
|2= 2. Tipp anzeigen | 3= 2. Tipp verbergen}} <br> | |||
{{Lösung versteckt |1= '''Lösung der Aufgabe:''' <br> | |||
Berechne zuerst den Flächeninhalt A! <br> | |||
A = a•h<sub>a</sub> =5,7cm •2,5cm = 14,25cm² <br> | |||
'''NR:''' <math> 57\cdot 25 = 1425 </math>, da die beiden Faktoren zusammen zwei Nachkommastellen haben, ist das Ergebnis für den Flächeninhalt 14,25 cm². Vergiss bitte nicht "<math> cm \cdot cm = cm^2 </math>"! <br> | |||
Nun weiß man, dass A = 14,25 cm². Man kennt auch die Seitenlänge der anderen Seite des Parallelogramms: b = 3,5 cm. <br> | |||
Den Flächeninhalt des Parallelogramms könnte man auch bestimmen, indem man A = b•h<sub>b</sub> berechnet. <br> | |||
Damit kann man nun die zur Seite b gehörige Höhe mit Hilfe einer Umkehrrechnung wie folgt berechnen: <br> h<sub>b</sub> = A : b = 14,25 cm² : 3,5 cm = 142,5 cm² : 35 cm = 4,0714... cm ≈ 4,1 cm. <br> Vergiss bitte nicht "<math> cm^2 \div cm = cm </math>"! Das Ergebnis muss eine Länge sein! <br> | |||
'''Anmerkung:''' <br> | |||
Das richtige Endergebnis bei dieser Aufgabe zu berechnen ist ehrlich gesagt gar nicht so wichtig, hier zählt es mehr den Rechenweg verstanden zu haben. <br> Hier noch einmal kurz zusammengefasst: Man berechnet zunächst mit der Seitenlänge a = 5,7 cm und der zugehörigen Höhe h<sub>a</sub>=2,5 cm den Flächeninhalt A des Parallelogramms und mit der Kenntnis dieses Flächeninhalts kann man nun h<sub>b</sub> mit Hilfe einer Umkehraufgabe berechnen, indem man "A : b" berechnet und als Ergebnis die Höhe h<sub>b</sub> erhält. | |||
|2= Lösung anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box |1= Test und Hausaufgabe: |2= '''B.S.142/ 18''' <br> Tipp: Eine Skizze kann für einen ersten Überblick hilfreich sein, zeichne gegebene Längen in die Skizze mit Farbe ein. <br> '''WICHTIG:''' Lade bitte die Lösung deiner Hausaufgabe im Schulmanager - Modul Lernen hoch! Danke! Ich würde gerne einmal einen Blick darauf werfen... | |||
|3= Üben}} | |||
==25.02.2021== | |||
{{Box |1= Übung: |2= Bevor du startest wiederhole bitte für dich die Formel zur Berechnung des Flächeninhalts eines Parallelogramms und auch die Formel zur Berechnung seines Umfangs. Solltest du heute dabei feststellen, dass etwas unklar ist, dann schau dir bitte das entsprechende Erklärvideo an. Danke! <br> Wenn alles klar ist, dann geht's los - heute zunächst noch einmal eine Aufgabe zu Parallelogrammen... <br> | |||
'''Bearbeite bitte im Buch S. 141/ 10 c) und d)!''' <br> Bei dieser Aufgabe musst du zunächst die Parallelogramme in ein Koordinatensystem zeichnen, falls du dich nicht mehr so genau daran erinnern kannst, wie man einen Punkt in ein Koordinatensystem einträgt, hilft die das nach der Lösung angefügte Video weiter... Schau dir dieses dann bitte an, bevor du mit der Lösung der Aufgaben beginnst. <br> | |||
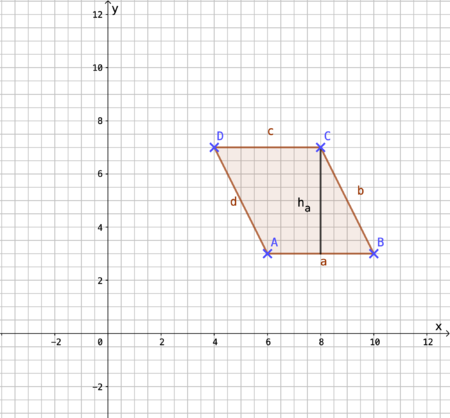
{{Lösung versteckt|1=[[Datei:141-10c.png|141-10c.png|450px]]A = a • h<sub>a</sub> = 4 cm • 4 cm = 16 cm² |2=10c Aufdecken|3=Verbergen}} | |||
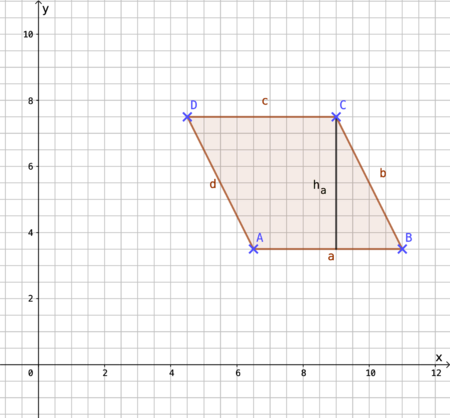
{{Lösung versteckt|1=[[Datei:141-10d.png|141-10d.png|450px]]A= a • h<sub>a</sub> = 4,5 cm • 4 cm = 18 cm² |2=10d Aufdecken|3=Verbergen}} | |||
|3= Üben}} | |||
{{Box| Falls du Hilfe benötigst - Punkte im Koordinatensystem: |{{#ev:youtube|watch?v=3x9R2uFSMds|600|center}} | Hervorhebung1}} | |||
{{Box|1= Zur Erinnerung: |2= Ein Dreieck hat drei Eckpunkte, welche man meistens mit A, B und C bezeichnet. <br> Weitere Bezeichnungen am Dreieck: <br> Winkel <math>\alpha</math> liegt am Eckpunkt A, gegenüber vom Punkt A liegt die Seite a, Winkel <math>\beta</math> liegt am Eckpunkt B, gegenüber von Punkt B liegt die Seite b und Winkel <math>\gamma</math> liegt am Eckpunkt C, gegenüber vom Punkt C liegt die Seite c. <br> Mit folgendem Link kannst du dir die Beschreibung von eben bezüglich der Bezeichnungen am Dreieck noch einmal bildhaft verdeutlichen: [https://upload.wikimedia.org/wikipedia/commons/thumb/d/dd/Dreieck.svg/456px-Dreieck.svg.png Notationen am Dreieck] | 3= Arbeitsmethode}} | |||
{{Box|1= Idee: |2= Herleitung der Formel zur Berechnung des '''Flächeninhalts A eines Dreiecks'''. <br> | |||
Um den Flächeninhalt eines Dreiecks bestimmen zu können, erinnert man sich zunächst an die Berechnung des Flächeninhalts eines Rechtecks <math>A= a \cdot b</math>, a beschreibt die Länge und b die Breite des Rechtecks. <br> Vielleicht hast du auch schon eine Idee, wie man den Flächeninhalt eines Dreiecks mit dem Wissen zur Berechnung des Flächeninhalts eines Rechtecks bestimmen kann? <br> Bevor du dir den entsprechenden Merksatz in dein Heft notieren wirst, schau dir im Folgenden Schritt für Schritt eine der Möglichkeiten an, wie der Flächeninhalt eines Dreiecks bestimmt werden kann. <br> Am Montag wirst du noch eine andere Idee kennen lernen, aber das Ergebnis ist dasselbe wie heute, die Formel zur Berechnung des Flächeninhalts eines Dreiecks bleibt gleich... <br> Falls du nur "GeoGebra" lesen kannst, aktualisiere bitte die Internetseite - z.B. indem du "F5" auf der Tastatur drückst, dann sollte es normalerweise klappen... | |||
<ggb_applet id="tT6Yj7Dg" width="800" height="450" border="888888" /> | |||
<br> | |||
<br> | |||
|3= Unterrichtsidee}} | |||
{{Box|1= Wichtig: |2= Zur Berechnung des Flächeninhalts eines Dreiecks muss man die Höhen im Dreieck kennen, zu jeder Seite im Dreieck gibt es eine zugehörige Höhe, dies ist der Abstand eines Eckpunktes von seiner gegenüberliegenden Seite. Der Abstand ist die kürzeste Strecke vom Eckpunkt aus auf die Seite und steht deswegen auf der gegenüberliegenden Seite senkrecht... Insgesamt gibt es also drei Höhen im Dreieck.... diese können aber auch außerhalb des Dreiecks liegen: | |||
| 3= Unterrichtsidee}} | |||
{{Box| Höhen im Dreieck: |{{#ev:youtube|watch?v=nRJnWvPuuuQ|600|center}} | Hervorhebung1}} | |||
{{Box|Merke:|Schreibe nun zunächst '''Flächeninhalt eines Dreiecks''' als Überschrift in dein Heft und notiere dir anschließend den Merksatz zu Höhen im Dreieck! <br> Zeichne ein spitzwinkliges Dreieck, in dem du alle drei Höhen, wie im vorgehenden Erklärvideo gesehen einzeichnest. <br> Falls du nun merkst, dass beim Zeichnen noch etwas unklar ist, dann schau dir einfach nochmal die entsprechende Stelle im Video an oder melde dich bei mir in der Videosprechstunde... | |||
{{Lösung versteckt|1= | |||
'''Höhen im Dreieck:'''<br> | |||
Unter den Höhen eines Dreiecks versteht man die Abstände der Eckpunkte von den gegenüberliegenden Seiten bzw. deren Verlängerungen (im Falle eines stumpfwinkligen Dreiecks). <br> Ein Dreieck hat drei Höhen. <br> | |||
''Beispiel:'' h<sub>c</sub> ist der Abstand des Eckpunktes C von der Seite <math> \overline{AB} </math> bzw. deren Verlängerung. | |||
<br> | |||
|2=Aufdecken|3=Verbergen}} | |||
|3=Merksatz}} | |||
{{Box|Merke: |Vervollständige deinen Hefteintrag mit dem folgenden Merksatz! <br> | |||
{{Lösung versteckt|1= | |||
'''Flächeninhalt eines Dreiecks'''<br> | |||
Der Flächeninhalt A eines Dreiecks ist gleich die Hälfte des Produkts aus der Seitenlänge und der '''zugehörigen''' Höhe.<br> | |||
'''<math> A = \frac {1}{2} \cdot a \cdot h_a </math> ''' oder '''<math> A = \frac {1}{2} \cdot b \cdot h_b </math>''' oder '''<math> A = \frac {1}{2} \cdot c \cdot h_c </math>'''; <br> '''Allgemein gilt:''' '''<math> A = \frac {1}{2} \cdot g \cdot h = \frac {g\cdot h}{2} = (g\cdot h) \div2 </math>''', der Flächeninhalt ist die Hälfte des Produkts aus einer Seite (Grundseite g) und zugehöriger Höhe (h).<br> | |||
Folgende Anmerkung ist nur eine Anmerkung und nicht Teil des Hefteintrags... <br> | |||
Anmerkung: Unter "allgemein gilt" konntest du der Vollständigkeit halber auch andere Notationsvarianten für den Flächeninhalt eines Dreiecks kennen lernen. Bei der Bearbeitung einer Aufgabe verwendet man meist die Formel <math> A = \frac {1}{2} \cdot g \cdot h </math> als Ansatz, die anderen Formeln helfen im weiteren Verlauf der Rechnung dabei richtig zu berechnen... | |||
|2=Aufdecken |3= Verbergen}} | |||
|3=Merksatz}} | |||
{{Box |1= Übung und Hausaufgabe: |2= Ein kleiner Test zum Verständnis des Flächeninhalts des Dreiecks... Bearbeite B. S. 135/ 4a), b) und d)! Überlege dir jeweils genau, was ist die Seite des Dreiecks, wie lang ist diese und was die zugehörige Höhe. Vergleiche im Anschluss bitte deine Lösung mit meinem Lösungsvorschlag. <br> '''Erinnerung:''' Notiere dir stets, was gegeben ist und schreibe auch immer die Formel auf, die du zur Bearbeitung der Aufgabe verwendest. | |||
{{Lösung versteckt |1= '''Lösung der Aufgaben:''' <br> | |||
'''a)''' <br> | |||
g = 9 cm und h = 4 cm <br> | |||
<math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 9 cm \cdot 4 cm = \frac{1}{2} \cdot (9 cm \cdot 4 cm) = \frac {1}{2} \cdot 36 cm^2 = 18 cm^2 </math> <br> | |||
'''b)''' <br> | |||
g = 6 cm und h = 4 cm oder aber auch g = 4 cm und h = 6 cm, denn zwei Seiten des Dreiecks stehen aufeinander senkrecht. Damit ist die eine Seite die Höhe zu der Seite, auf der sie senkrecht steht oder eben umgekehrt...<br> | |||
<math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 6 cm \cdot 4 cm = \frac{1}{2} \cdot (6 cm \cdot 4 cm) = \frac {1}{2} \cdot 24 cm^2 = 12 cm^2 </math> <br> | |||
'''d)''' <br> | |||
ACHTUNG: g = 3,5 cm und h = 2,7 cm <br> | |||
<math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 3,5 cm \cdot 2,7 cm = \frac{1}{2} \cdot (3,5 cm \cdot 2,7 cm) = \frac {1}{2} \cdot 9,45 cm^2 = 9,45 cm^2 \div 2= 4,725 cm^2 </math> <br> Anmerkung: "<math> \frac{1}{2} \cdot </math>" entspricht "geteilt durch 2", was manchmal leichter im Kopf zu berechnen ist.... Man bestimmt ja letztendlich die Hälfte...<br> | |||
|2= Lösung der Aufgabe anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |3= Üben}} | ||
Aktuelle Version vom 27. Februar 2021, 19:05 Uhr
15.02.2021
17.02.2021
18.02.2021
22.02.2021
24.02.2021
25.02.2021