6e Lernen zu Hause: Brüche und Dezimalbrüche: Unterschied zwischen den Versionen
Aus RMG-Wiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 414: | Zeile 414: | ||
{{Box| Höhen im Dreieck: |{{#ev:youtube|watch?v=nRJnWvPuuuQ|600|center}} | Hervorhebung1}} | {{Box| Höhen im Dreieck: |{{#ev:youtube|watch?v=nRJnWvPuuuQ|600|center}} | Hervorhebung1}} | ||
{{Box|Merke:| | {{Box|Merke:|Schreibe nun zunächst '''Flächeninhalt eines Dreiecks''' als Überschrift in dein Heft und notiere dir anschließend den Merksatz zu Höhen im Dreieck! <br> Zeichne ein spitzwinkliges Dreieck, in dem du alle drei Höhen, wie im vorgehenden Erklärvideo gesehen einzeichnest. <br> Falls du nun merkst, dass beim Zeichnen noch etwas unklar ist, dann schau dir einfach nochmal die entsprechende Stelle im Video an oder melde dich bei mir in der Videosprechstunde... | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
'''Höhen im Dreieck:'''<br> | '''Höhen im Dreieck:'''<br> | ||
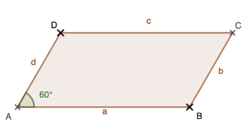
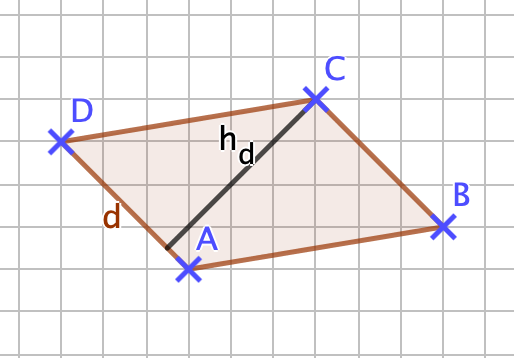
Unter den Höhen eines Dreiecks versteht man die Abstände der Eckpunkte von den gegenüberliegenden Seiten bzw. deren Verlängerungen (im Falle eines stumpfwinkligen Dreiecks). Ein Dreieck hat drei Höhen. <br> | Unter den Höhen eines Dreiecks versteht man die Abstände der Eckpunkte von den gegenüberliegenden Seiten bzw. deren Verlängerungen (im Falle eines stumpfwinkligen Dreiecks). <br> Ein Dreieck hat drei Höhen. <br> | ||
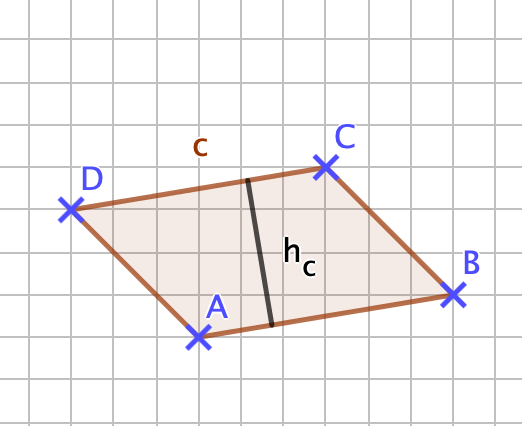
''Beispiel:'' | ''Beispiel:'' h<sub>c</sub> ist der Abstand des Eckpunktes C von der Seite <math> \overline{AB} </math> bzw. deren Verlängerung. | ||
<br> | <br> | ||
|2=Aufdecken|3=Verbergen}} | |2=Aufdecken|3=Verbergen}} | ||
| Zeile 427: | Zeile 427: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
'''Flächeninhalt eines Dreiecks'''<br> | '''Flächeninhalt eines Dreiecks'''<br> | ||
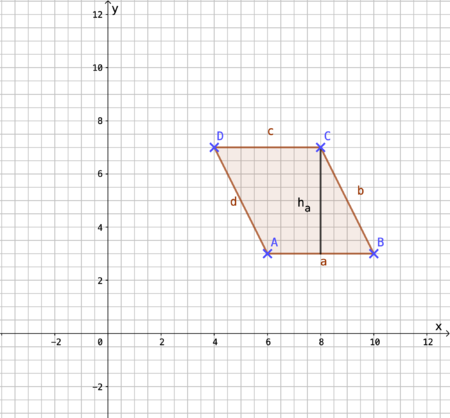
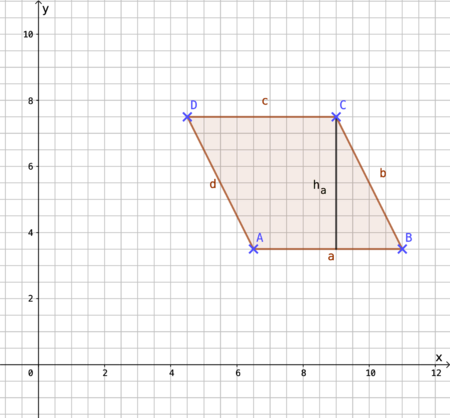
Der Flächeninhalt A eines Dreiecks | Der Flächeninhalt A eines Dreiecks ist gleich der Hälfte des Produkts aus der Seitenlänge und der '''zugehörigen''' Höhe.<br> | ||
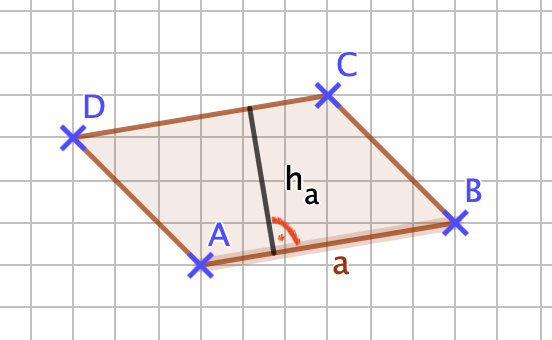
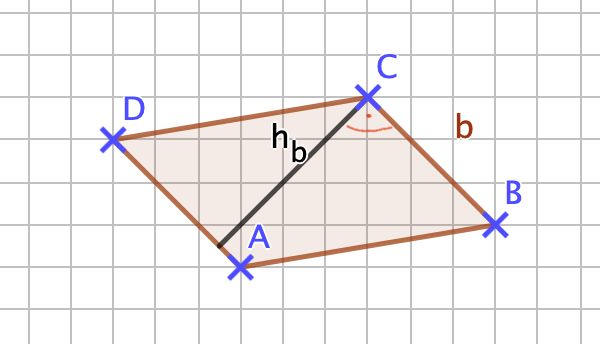
'''<math> A = \frac {1}{2} \cdot a \cdot h_a </math> ''' oder '''<math> A = \frac {1}{2} \cdot b \cdot h_b </math>''' oder '''<math> A = \frac {1}{2} \cdot c \cdot h_c </math>'''; | '''<math> A = \frac {1}{2} \cdot a \cdot h_a </math> ''' oder '''<math> A = \frac {1}{2} \cdot b \cdot h_b </math>''' oder '''<math> A = \frac {1}{2} \cdot c \cdot h_c </math>'''; <br> '''Allgemein gilt:''' '''<math> A = \frac {1}{2} \cdot g \cdot h </math>''', der Flächeninhalt ist die Hälfte des Produkts aus einer Seite (Grundseite g) und zugehöriger Höhe (h).<br> | ||
|2=Aufdecken |3= Verbergen}} | |2=Aufdecken |3= Verbergen}} | ||
| Zeile 434: | Zeile 434: | ||
{{Box |1= Übung: |2= Bearbeite B. S. 135/ 4a) und d)! Überlege dir jeweils genau, was ist die Seite des Dreiecks, wie lang ist diese und was die zugehörige Höhe. Vergleiche im Anschluss bitte deine Lösung mit meinem Lösungsvorschlag. <br> '''Erinnerung:''' Notiere dir stets, was gegeben ist und schreibe auch immer die Formel auf, die du zur Bearbeitung der Aufgabe verwendest. | |||
{{Lösung versteckt |1= '''Lösung der Aufgaben:''' <br> | |||
'''a)''' <br> | |||
g = 9 cm und h = 4 cm <br> | |||
<math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 9 cm \cdot 4 cm = \frac{1}{2} \cdot (9 cm \cdot 4 cm) = \frac {1}{2} 36 cm^2 = 18 cm^2 </math> <br> | |||
'''c)''' <br> | |||
ACHTUNG: g = 3,5 cm und h = 2,7 cm <br> | |||
<math> A = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot 3,5 cm \cdot 2,7 cm = \frac{1}{2} \cdot (3,5 cm \cdot 2,7 cm) = \frac {1}{2} 9,45 cm^2 = "9,45 cm^2 \div 2" = 4,725 cm^2 </math> <br> Anmerkung: "<math> \frac{1}{2} \cdot </math>" entspricht "geteilt durch 2", was so manchmal leichter im Kopf zu berechnen ist.... Man bestimmt ja letztendlich die Hälfte...<br> | |||
|2= Lösung der Aufgabe anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
Version vom 21. Februar 2021, 13:55 Uhr
15.02.2021
17.02.2021
18.02.2021
22.02.2021
24.02.2021
25.02.2021