6e Lernen zu Hause: Brüche und Dezimalbrüche: Unterschied zwischen den Versionen
Aus RMG-Wiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 114: | Zeile 114: | ||
=18.02.2021= | =18.02.2021= | ||
{{Box|1=Zur Wiederholung:|2= Erinnere dich an die Formel zur Berechnung des Flächeninhalts eines Rechtecks! Berechne nun den Flächeninhalt eines Rechtecks mit den Seiten a = 3 cm und b = 5 cm!{{Lösung versteckt |1= '''Anmerkung:''' <br> | {{Box|1=Zur Wiederholung:|2= Bevor es los geht, notiere zuerst '''Flächeninhalt eines Parallelogramms''' als Überschrift in dein Schulheft! <br> Erinnere dich an die Formel zur Berechnung des Umfangs eines Rechtecks! Berechne nun den Umfang eines Rechtecks mit den Seiten a = 3 cm und b = 5 cm! | ||
{{Lösung versteckt |1= '''Anmerkung:''' <br> | |||
Den Umfang eines Rechtecks erhält man, indem man in einem Eckpunkt des Rechtecks, z.B. A, "los läuft und einmal alle Seitenlängen des Rechteck abschreitet, bis man wieder zum Eckpunkt A gelangt"... <br> Um den Umfang eines Rechtecks bestimmen zu können addiert man alle Seitenlängen des Rechtecks, d.h. <math\>c\dot b </math> oder aber auch <math>A= a \cdot b </math>, je nachdem, welche Bezeichnung für die Seitenlängen des Rechtecks gewählt wurde... <br> | |||
'''Nun zu Lösung der Aufgabe:''' | |||
<math> A = a \cdot b= 3 cm \cdot 5 cm = 15 cm ^2 </math> | |||
|2= Lösung der Aufgabe anzeigen | 3= Lösung verbergen}} <br> | |||
|3=Üben}} | |||
{{Box|1=Zur Wiederholung:|2= Bevor es los geht, notiere zuerst '''Flächeninhalt eines Parallelogramms''' als Überschrift in dein Schulheft! <br> Erinnere dich an die Formel zur Berechnung des Flächeninhalts eines Rechtecks! Berechne nun den Flächeninhalt eines Rechtecks mit den Seiten a = 3 cm und b = 5 cm!{{Lösung versteckt |1= '''Anmerkung:''' <br> | |||
Der Flächeninhalt eines Rechtecks wird berechnet, indem man "Länge mal Breite" rechnet, d.h. <math> A= l \cdot b </math> oder aber auch <math>A= a \cdot b </math>, je nachdem, welche Bezeichnung für die Seitenlängen des Rechtecks gewählt wurde... <br> | Der Flächeninhalt eines Rechtecks wird berechnet, indem man "Länge mal Breite" rechnet, d.h. <math> A= l \cdot b </math> oder aber auch <math>A= a \cdot b </math>, je nachdem, welche Bezeichnung für die Seitenlängen des Rechtecks gewählt wurde... <br> | ||
| Zeile 124: | Zeile 135: | ||
|3=Üben}} | |3=Üben}} | ||
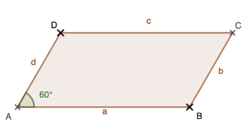
{{Box|1=Zum Einstieg: |2= | {{Box|1=Zum Einstieg: |2= <br> [[Datei:Parallelogramm Skizze.png|250px|right]] | ||
Nun | Nun geht es endlich los, du versuchst herauszufinden, wie der Flächeninhalt eines Parallelogramms bestimmt werden kann. Dazu benötigst du ein Blatt Papier - gerne bunt - eine Schere, einen Stift, ein Geodreieck und eine gute Idee... <br> | ||
Zeichne ein Parallelogramm ABCD mit der Länge a= | Zeichne ein Parallelogramm ABCD mit der Länge a = 9 cm und d = 5 cm sowie α = 60°. <br> Versuche nun den Flächeninhalt des Parallelogramms zu bestimmen! <br> | ||
|3=Frage}} | |3=Frage}} | ||
Version vom 16. Februar 2021, 19:36 Uhr
15.02.2021
17.02.2021
18.02.2021