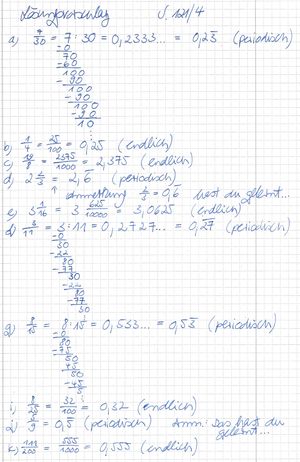6e Lernen zu Hause: Dezimalbrüchen: Unterschied zwischen den Versionen
Aus RMG-Wiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (32 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 142: | Zeile 142: | ||
{{Box |1= Videokonferenz: |2= Falls du wider Erwarten doch noch Fragen haben solltest, komm in die Videokonferenz, Link im Schulmanager - Modul Lernen, und stelle diese, falls alles klar ist, starte mit den Aufgaben.... Heute wird geübt, geübt und nochmal geübt... |3= Arbeitsmethode}} | {{Box |1= Videokonferenz: |2= Falls du wider Erwarten doch noch Fragen haben solltest, komm in die Videokonferenz, Link im Schulmanager - Modul Lernen, und stelle diese, falls alles klar ist, starte mit den Aufgaben.... Heute wird geübt, geübt und nochmal geübt... |3= Arbeitsmethode}} | ||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag B S | {{Box |1= Übung:|2= Wandle im Kopf um und ordne Brüche ihren Dezimalbrüchen oder eben Dezimalbrüche ihren Brüchen zu! <br> {{LearningApp|app=ptwujpy5v21|width=100%|height=700px}} | ||
|3= Arbeitsmethode}} | |||
{{Box |1= Übung:|2= Stelle einen Timer auf 15 Minuten und teste, wie viele Aufgaben du von B. S. 121/ 4 a) bis k) in dieser Zeit zu rechnen schaffst! '''WICHTIG:''' Lass bitte Teilaufgabe h) weg! Vielleicht brauchst du auch weniger als 15 Minuten... <br> '''Tipp:''' Du musst nicht immer alle Aufgaben durch Division lösen, vielleicht hilft Kürzen oder auch Erweitern auf 10, 100, 1000,... weiter. <br> Vielleicht siehst du bei einzelnen Aufgaben sofort, wie der Dezimalbruch sein muss, dann brauchst du erst gar nicht das Rechnen beginnen... <br> Verbessere bitte deinen Lösungsvorschlag! <br> Falls dein Ergebnis ein anderes sein sollte, vergleiche bitte deine Lösung Schritt für Schritt mit der von mir! Falls dir mein Lösungsvorschlag in der Darstellung zu klein sein sollte, kannst du einfach auf die beiden Rechtecke unten rechts im Bild klicken und es vergrößert sich.<br> | |||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag B S 121 4 a) bis k) ohne h).jpg|mini]] |2= Lösung Aufgabe 4 anzeigen | 3= Lösung verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Übung:| 2= Bearbeite B. S. 122/ 13 a) c) d) e) und vergleiche im Anschluss deine Lösung mit meiner! <br> | |||
{{Lösung versteckt |1=Die Zahlen von der kleinsten zur größten Zahl geordnet: <br> | |||
a) <math> 0,3 < 0,33 < 0,333 < 0,\overline {3} = 0,3333333333... < 0,334 </math> <br> | |||
c) <math> 0,6 < 0,7\overline {2} < \frac{3}{4} = 0,75 < 0,\overline{7} < 0,8 < \frac{7}{8} = 0,875 </math> <br> | |||
d) <math> \frac{1}{7} = 0,\overline{142857} < 0,57 < \frac{7}{10} = 0,7 < 0,\overline{71} < \frac {3}{4} = 0,75 < \frac{16}{20} = 0,8 </math> <br> | |||
e) <math> 0,16 < 0,166 < 0,1\overline{6} < 0,167 < 0,17 </math> <br> | |||
|2= Lösung Aufgabe 13 anzeigen | 3= Lösung verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Zur Wiederholung:| 2= Erinnerung: Bei 0, 1, 2, 3, 4 wird abgerundet, bei 5, 6, 7, 8, 9 wird aufgerundet. Bearbeite nun B. S. 122/ 10 b) und vergleiche anschließend deine Lösung mit meiner! <br> | |||
{{Lösung versteckt |1=Jeweils auf Tausendstel gerundet: <br> | |||
#<math> 0,\overline {5} = 0,5555555... \approx 0,556; </math> <br> | |||
#<math> 0,1\overline {6} = 0,1666666... \approx 0,167; </math> <br> | |||
#<math> 0,41\overline {6} = 0,41666666... \approx 0,417; </math> <br> | |||
#<math> 0,2\overline {7} = 0,2777777... \approx 0,278; </math> <br> | |||
#<math> 0,04\overline {5} = 0,0455555... \approx 0,046; </math> <br> | |||
#<math> 0,0\overline {45} = 0,04545454545... \approx 0,045; </math> <br> | |||
|2= Lösung Aufgabe 10 b) anzeigen | 3= Lösung verbergen}} | |||
|3= Üben}} | |3= Üben}} | ||
{{Box |1= Test:|2= Zum Überprüfen und weiteren Vertiefen deines gelernten Wissens kannst du hier '''freiwillig''' noch einmal Paare von Brüchen und Dezimalbrüchen passend zuordnen. Mit der folgenden LearningApp hast du die Möglichkeit zu testen, ob du besondere Brüche und ihre zugehörigen Dezimalzahlen bereits gut genug gelernt hast. Viel Freude dabei! <br> Der Test wäre ganz klar eine Empfehlung von mir an dich, um damit deinen Lernfortschiritt zu testen, vielleicht kannst du ihn ja heute noch zeitlich unterbringen... Ich würde mich freuen! <br> {{LearningApp|app=ppjjvkti321|width=100%|height=700px}} | |||
|3= Arbeitsmethode}} | |||
=11.02.2021= | =11.02.2021= | ||
| Zeile 156: | Zeile 195: | ||
{{Box |1= Verknüpfung von Brüchen und Dezimalbrüchen: |2= Sicher hast du es | {{Box |1= Verknüpfung von Brüchen und Dezimalbrüchen: |2= Bevor du los legst notiere dir '''Rechnen mit Brüchen und Dezimalbrüchen''' als Überschrift in dein Schulheft! <br> | ||
Sicher hast du es dir schon gedacht, es gibt Aufgaben, in den tauchen sowohl Brüche als auch Dezimalbrüche auf... Hier stellt sich nun die Frage, was ist zu tun? Hast du schon eine Idee? Falls nicht überlege mit Hilfe der folgenden Aufgabe, wie du dieses Problem sinnigerweise lösen würdest! <br> | |||
a) <math>0,75- \frac {1}{4} = </math> <br> | a) <math>0,75- \frac {1}{4} = </math> <br> | ||
b) <math>\frac{1}{8} \cdot 0,75 =</math> | b) <math>\frac{1}{8} \cdot 0,75 =</math> | ||
| Zeile 184: | Zeile 224: | ||
{{Lösung versteckt |1= '''Anmerkung:''' <br> | {{Lösung versteckt |1= '''Anmerkung:''' <br> | ||
Um Aufgaben mit Brüchen und Dezimalbrüchen berechnen zu können, ist es wichtig alle Zahlen der Aufgabe entweder in Brüche oder in Dezimalbrüche umzuwandeln! <br> '''Wichtig:''' Brüche, die nicht als endliche, sondern nur als unendliche - im Besonderen als periodische - Dezimalbrüche geschrieben werden können, sollte man für die Berechnung der jeweiligen Aufgabe '''nicht''' in Dezimalbrüche umwandeln. Hier sollte man stets mit Brüchen rechnen | Um Aufgaben mit Brüchen und Dezimalbrüchen berechnen zu können, ist es wichtig alle Zahlen der Aufgabe entweder in Brüche oder in Dezimalbrüche umzuwandeln! <br> '''Wichtig:''' Brüche, die nicht als endliche, sondern nur als unendliche - im Besonderen als periodische - Dezimalbrüche geschrieben werden können, sollte man für die Berechnung der jeweiligen Aufgabe '''nicht''' in Dezimalbrüche umwandeln. Hier sollte man stets mit Brüchen rechnen! <br> Beispielsweise sollte man in folgender Aufgabe <math> \frac{1}{3} </math> '''nicht''' in den Dezimalbruch <math> 0,\overline{3} </math> umwandeln, sondern wie folgt berechnen: <math> 0,8 \cdot \frac{1}{3} = \frac{4}{5} \cdot \frac{1}{3} = \frac {4}{15} </math> | ||
|2= Anmerkung anzeigen | 3= Anmerkung verbergen}} <br> | |2= Anmerkung anzeigen | 3= Anmerkung verbergen}} <br> | ||
|3= Merksatz}} | |3= Merksatz}} | ||
{{Box |1= Übung: |2= Bearbeite bitte im Buch S. 125/ 3) und 5)! <br> Vergleiche anschließend deine Lösung mit der von mir - hake richtige Lösungen ab und verbessere falsche! <br> | |||
{{Lösung versteckt |1= Lösung der Aufgaben: <br> | |||
Allgemeine Info zu Aufgabe 3: <br> In der Regel ist das Addieren und Subtrahieren von Dezimalbrüchen schneller. <br> In b), c), g), h) und j) kann man die Brüche nicht in endliche Dezimalbrüche umwandeln. Daher rechnet man hier mit Brüchen! <br> | |||
'''a)''' <br> | |||
<math>0,2 + 0,75 = 0,95 </math> oder aber auch | |||
<math>\frac {2}{10} + \frac {3}{4} = \frac{4}{20} + \frac{15}{20} = \frac {19}{20}</math> <br> | |||
'''b)''' <br> | |||
<math>0,2 + \frac{2}{3} = \frac{2}{10} + \frac {2}{3} = \frac{6}{30} + \frac {20}{30} = \frac{26}{30} = \frac{13}{15} </math> <br> | |||
'''c)''' <br> | |||
<math>0,75 - \frac{5}{12} = \frac{3}{4} - \frac{5}{12} = \frac{9}{12} - \frac{5}{12} = \frac{4}{12} = \frac{1}{3} </math> <br> | |||
'''d)''' <br> | |||
<math> 0,75 - \frac{1}{4} = 0,75 - 0,25 = 0,5 </math> oder aber auch | |||
<math> 0,75 - \frac{1}{4} = \frac{3}{4} - \frac{1}{4} = \frac{2}{4}= \frac {1}{2} </math> <br> | |||
'''e)''' <br> | |||
<math> \frac{1}{8} + 0,75 = 0,125 + 0,75 = 0,875 </math> oder aber auch | |||
<math> \frac{1}{8} + 0,75 = \frac {1}{8} + \frac{3}{4} = \frac{1}{8} + \frac{6}{8} = \frac{7}{8} </math> <br> | |||
'''f)''' <br> | |||
<math> \frac{1}{8} + 0,7 = 0,125 + 0,7 = 0,825 </math> oder aber auch | |||
<math> \frac{1}{8} + 0,7 = \frac{1}{8} + \frac{7}{10} = \frac{5}{40} + \frac{28}{40} = \frac{33}{40} </math> <br> | |||
'''g)''' <br> | |||
<math> \frac{1}{3} + 0,3 = \frac{1}{3} + \frac{3}{10} = \frac{10}{30} + \frac{9}{30} = \frac{19}{30} </math> <br> | |||
'''h)''' <br> | |||
<math> 0,7 + \frac{1}{15} = \frac{7}{10} + \frac{1}{15} = \frac{21}{30} + \frac{2}{30} = \frac{23}{30} </math> <br> | |||
'''i)''' <br> | |||
<math> 0,9 -\frac{3}{25}= 0,9 - \frac{12}{100} = 0,9 - 0,12 = 0,78 </math> oder aber auch | |||
<math> 0,9 - \frac{3}{25} = \frac{9}{10} - \frac{3}{25} = \frac{45}{50} - \frac{6}{50} = \frac{39}{50} </math> <br> | |||
'''j)''' <br> | |||
<math> \frac{7}{9} - 0,3 = \frac{7}{9} - \frac{3}{10} = \frac{70}{90} - \frac{27}{90} = \frac{43}{90} </math> | |||
|2= Lösung der Aufgabe 3 anzeigen | 3= Lösung verbergen}} <br> | |||
{{Lösung versteckt |1= Lösung der Aufgaben: <br> | |||
'''a)''' <br> | |||
Jonas hat mit Brüchen und Linda mit Dezimalbrüchen gerechnet. <br> | |||
'''b)''' <br> | |||
(1) <math> 15 \cdot 0,7 l = 10,5 l </math> oder <math> 15 \cdot \frac{7}{10} l = \frac { 15 \cdot 7}{10} l = \frac{105}{10} l = 10 \frac{5}{10} l = 10 \frac{1}{2} l </math> <br> Im Keller befinden sich insgesamt 10,5 l Wasser. <br> | |||
(2) <math>4 \cdot \frac{3}{8} l = \frac { 4 \cdot 3}{8} l = \frac{3}{2} l </math> oder <math> 4 \cdot \frac {3}{8} l = 4 \cdot \frac{375}{1000} l = 4 \cdot 0,375 l = 1,5 l </math> <br> Für die vier Kuchen benötigt Franziska 1,5 Liter Sahne. <br> | |||
|2= Lösung der Aufgabe 5 anzeigen | 3= Lösung verbergen}} <br> | |||
|3= Üben}} | |||
{{Box |1= Freiwillig: |2= Falls du noch Lust hast, kannst du hier nochmal die Zusammenhänge zwischen Brüchen, Dezimalzahlen und Prozentzahlen wiederholen. <br> {{LearningApp|app=1574798|width=100%|height=700px}} | |||
|3= Arbeitsmethode}} | |||
Aktuelle Version vom 8. Februar 2021, 09:31 Uhr
08.02.2021
10.02.2021
11.02.2021