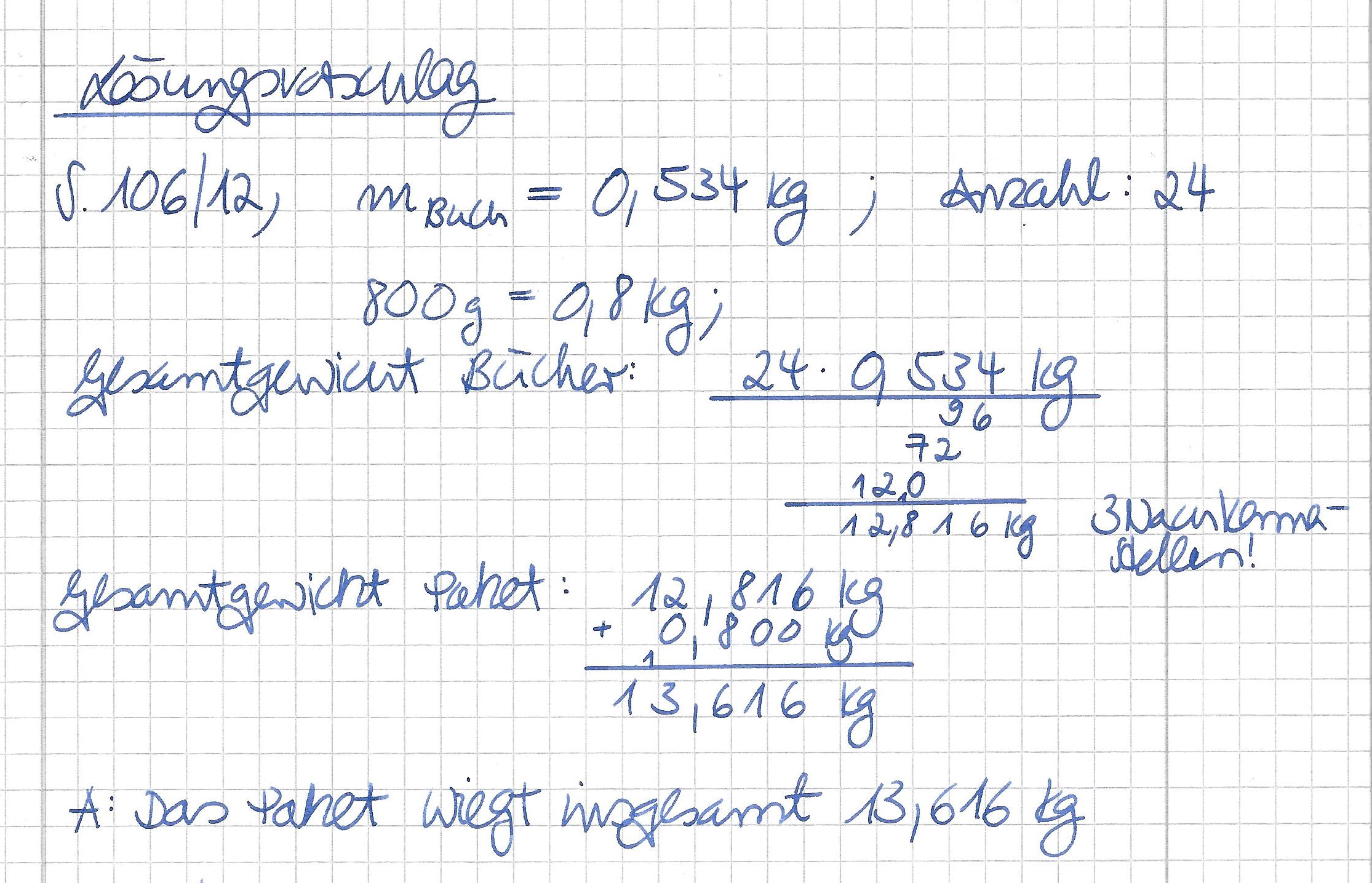6e Lernen zu Hause: Multiplizieren von Dezimalbrüchen mit Stufenzahlen und Dividieren durch Stufenzahlen: Unterschied zwischen den Versionen
Aus RMG-Wiki
Markierung: 2017-Quelltext-Bearbeitung |
Markierung: 2017-Quelltext-Bearbeitung |
||
| (39 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 35: | Zeile 35: | ||
{{Box |1= | {{Box |1= Übung 1: |2= Bearbeite bitte im Buch S. 102/ 3 - jedoch nur für Stellenwert der Ziffer 7! <br> Verbessere deine Lösung in ROT! | ||
{{Lösung versteckt |1= | |||
a) Multipliziert mit: <br> | |||
* 10: Zehntel | |||
* 100: Einer | |||
* 1000: Zehner | |||
*10000: Hunderter <br> | |||
b) Dividiert durch: <br> | |||
* 10: Tausendstel | |||
* 100: Zehntausendstel | |||
* 1000: Hunderttausendstel | |||
* 10000: Millionstel | |||
|2= Lösung Aufgabe 3 anzeigen | 3= Lösung verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Übung 2: |2= Bearbeite bitte im Buch S. 102/ 4! <br> Verbessere deine Lösung in ROT! | |||
{{Lösung versteckt |1= | |||
a) 0,024 <br> | |||
b) 3,6 <br> | |||
c) 71 <br> | |||
d) 0,086 <br> | |||
e) 0,00371 <br> | |||
f) 0,00065 <br> | |||
Anmerkung zu Teilaufgabe 4 f): <br> Ein Hunderttausendstel von 65, d.h. man rechnet 65 (man könnte für 65 auch 65,0 notieren) geteilt durch 100000 - das bedeutet "man geht" 5 Stellen nach links... um dies tun zu können, muss man zunächst auf der linken Seite von 65 Nullen ergänzen, d.h. man rechnet im Endeffekt 000065: 100000 = 0,00065 und schiebt das (nicht vorhandene) Komma von rechts eine Stelle nach links zwischen die 6 und die 5, dann eine zweite Stelle nach links zwischen 0 und 6 und so weiter, bis man alle 5 Stellen "gegangen ist"... und erhält dann als Ergebnis 0,00065 | |||
|2= Lösung Aufgabe 4 anzeigen | 3= Lösung verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Übung 3: |2= Bearbeite bitte im Buch S. 102/ 5! <br> Verbessere deine Lösung in ROT! | |||
{{Lösung versteckt |1= | |||
a) <math>60 mm \div 1000 = 0060 mm : 1000 = 0,06 mm</math> <br> Anmerkung: Man verschiebt das Komma drei Stellen links. <br> Antwortsatz: Das menschliche Haar ist in Wirklichkeit 0,06 mm dick. <br> | |||
b) <math> 0,005 mm \cdot 1000 = 5 mm </math> <br> Anmerkung: Man verschiebt das Komma drei Stellen nach rechts. <br> Antwortsatz: Der Spinnwebfaden erscheint 5 mm dick. | |||
|2= Lösung Aufgabe 5 anzeigen | 3= Lösung verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Übung 4: |2= Bearbeite bitte im Buch S. 102/7 b)! <br> Verbessere deine Lösung in ROT! | |||
{{Lösung versteckt |1= | |||
* <math> 0,933 \div 10 = 0,0933 </math> | |||
* <math> 0,933 \cdot 100 = 93,3 </math> | |||
* <math> 0,0933 \cdot 1000 = 93,3 </math> | |||
*<math> 930 \div 10000 = 0,093 </math> | |||
|2= Lösung Aufgabe 7 anzeigen | 3= Lösung verbergen}} | |||
|3= Üben}} | |||
{{Box |1= Hausaufgabe: |2= Bearbeite B. S. 102/ 2 - hier geht es um Kopfrechnen... <br> | |||
Wenn du magst, berechne doch die Aufgaben am Telefon gemeinsam mit jemanden aus deiner Klasse... <br> ODER <br>Berechne die Aufgaben alleine und besprich diese im Anschluss mit jemanden aus deiner Klasse z.B. am Telefon... <br> Gemeinsam über Mathe reden hilft ungemein beim Verständnis. <br> ODER <br> Berechne alleine die Aufgaben... <br> | |||
Auf jeden Fall möchte ich heute deine Lösungen/ eure Lösungen anschauen, deswegen lade mir die heutige Hausaufgabe im Schulmanager hoch - bitte vermerke mir, wenn du die Aufgaben mit jemanden gemeinsam gelöst oder bereits besprochen hast! Deine erste Lösung sollte immer noch für mich erkennbar sein, aber du weißt ja, dass du mit ROT korrigieren sollst. Danke! | |||
|3= Üben}} | |3= Üben}} | ||
=27.01.2021: Multiplizieren von Dezimalbrüchen= | |||
{{Box|1= Neu: |2= Nicht verrückt machen, wenn du Schriftlich Multiplizieren und auch noch zählen kannst, sollte das Multiplizieren von Dezimalbrüchen kein Problem werden. Sieh dir nun zunächst folgendes Video aufmerksam an!| 3= Arbeitsmethode}} | |||
{{Box| Multiplizieren von Dezimalbrüchen: |{{#ev:youtube|watch?v=2QfdWJMQpUU|600|center}} | Hervorhebung1}} | |||
{{Box |1= Zur Kontrolle: |2= Nun bist du an der Reihe! Berechne nun nochmal alleine die beiden Aufgaben aus dem Video! | |||
*Berechne <math> 8,3 \cdot 1,4 </math>! | |||
{{Lösung versteckt|1= <math> = 11,62</math> <br> WICHTIG: Die Zahl 8,3 hat eine Nachkommastelle, ebenso die Zahl 1,4. <br> Somit hat das Ergebnis der Multiplikation zwei Nachkommastellen, denn "1 Nachkommastelle + 1 Nachkommastelle = 2 Nachkommastellen"! |2=Aufdecken|3=Verbergen}} | |||
*Berechne <math> 31,4 \cdot 1,21</math>! | |||
{{Lösung versteckt|1= <math> = 37,994 </math> <br> WICHTIG: Die Zahl 31,4 hat eine Nachkommastelle, die Zahl 1,21 hat zwei Nachkommastellen. <br> Da "1 Nachkommastelle + 2 Nachkommastellen = 3 Nachkommastellen", hat das Ergebnis der Multiplikation drei Nachkommastellen... |2=Aufdecken|3=Verbergen}} | |||
Falls nun noch etwas unklar sein sollte oder deine Lösungen so ganz anders als meine, dann schau dir bitte nochmal obiges Video an und rechne Schritt für Schritt mit Lehrer Schmidt ;-) | |||
|3= Üben}} | |||
{{Box|1= Und alles klar? |2= Notiere bitte noch folgenden Merksatz in dein Heft! <br> | |||
<u>'''Merke: Regel für die Multiplikation von Dezimalbrüchen'''</u> <br> | |||
# Multipliziere zunächst so, als wäre kein Komma vorhanden - Stichwort: schriftlich Multiplizieren! | |||
# Setze dann im Ergebnis das Komma so, dass rechts vom Komma so viele Zahlen stehen, wie die beiden Faktoren zusammen nach dem Komma haben! | |||
|3= Merksatz}} | |||
{{Box |1= Zur Vertiefung: |2= Berechne folgende Aufgaben! | |||
*B.S.106/ 19 a): Berechne <math> 30,8 \cdot 0,29 </math>! | |||
{{Lösung versteckt|1= <math> =8,932 </math> <br> WICHTIG: Berechne zunächst schriftlich <math> 308 \cdot 29 </math>. Das Ergebnis hier ist 8932. <br> Die Zahl 30,8 hat eine Nachkommastelle, die Zahl 0,29 hat zwei Nachkommastellen. <br> Somit hat das Ergebnis der Multiplikation drei Nachkommastellen, denn "1 Nachkommastelle + 2 Nachkommastellen = 3 Nachkommastellen"! |2=Aufdecken|3=Verbergen}} | |||
*B.S.106/ 19 e): Berechne <math> 9,93 \cdot 0,19</math>! | |||
{{Lösung versteckt|1= <math> = 1,8867 </math> <br> WICHTIG: Berechne zunächst schriftlich <math> 993 \cdot 19</math>. Das Ergebnis hier ist 18867. <br> Die Zahl 9,93 hat zwei Nachkommastellen, die Zahl 0,19 hat zwei Nachkommastellen. <br> Da "2 Nachkommastellen + 2 Nachkommastellen = 4 Nachkommastellen", hat das Ergebnis der Multiplikation vier Nachkommastellen... |2=Aufdecken|3=Verbergen}} | |||
*B.S.106/ 19 l): Berechne <math> 0,508 \cdot 53,6</math>! | |||
{{Lösung versteckt|1= <math> = 27,2288 </math> <br> WICHTIG: Berechne zunächst schriftlich <math> 508 \cdot 536 </math>. Das Ergebnis hier ist 272288. <br> Die Zahl 0,508 hat drei Nachkommastellen, die Zahl 53,6 hat eine Nachkommastelle. <br> Da "3 Nachkommastellen + 1 Nachkommastelle = 4 Nachkommastellen", hat das Ergebnis der Multiplikation vier Nachkommastellen... |2=Aufdecken|3=Verbergen}} | |||
|3= Üben}} | |||
{{Box|1= Übung:| 2= Bearbeite bitte folgende Aufgaben im Schulheft: B. S. 105/ 12, 15 und 17 b) | |||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag 106 12.jpg]] |2= Lösung Aufgabe 12 anzeigen | 3= Lösung verbergen}} | |||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag 106 15.jpg]] |2= Lösung Aufgabe 15 anzeigen | 3= Lösung verbergen}} | |||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag 106 17b.jpg]] |2= Lösung Aufgabe 17 b) anzeigen | 3= Lösung verbergen}} | |||
|3= Üben}} | |||
=28.01.2021: Multiplizieren von Dezimalbrüchen= | |||
{{Box| 1= Zur Wiederholung: | | |||
2= Notiere in der Lösungszeile nur die Zahl, die in die gelb markierte Lücke notiert werden muss, beachte dabei auch die "Gemerkten". <br> | |||
{{LearningApp|app=12302944|width=100%|height=700px}} | |||
|3 = Arbeitsmethode}} | |||
{{Box| 1= Zum Einstieg noch etwas Kopfrechnen...: | | |||
2= {{LearningApp|app=4293413|width=100%|height=700px}} | |||
|3 = Arbeitsmethode}} | |||
{{Box|1= Kommaverschiebung für Produkte: |2= Bearbeite bitte B. S. 104/ 2! Übertrage bitte auch den roten Kasten als Merksatz in dein Schulheft während du die Aufgabe bearbeitest ! | |||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag B S 104 2.jpg]] |2= Lösung Aufgabe 2 anzeigen | 3= Lösung verbergen}} | |||
| 3= Arbeitsmethode}} | |||
{{Box|1= Übung: |2= Bearbeite bitte B. S. 105/ 7 b), c) und 11! | |||
{{Lösung versteckt |1=[[Datei:Lösungsvorschlag B S 105 7b c 11.jpg|Lösungsvorschlag B S 105 7b c 11.jpg]] |2= Lösung Aufgabe 7 und 11 anzeigen | 3= Lösung verbergen}} | |||
| 3= Arbeitsmethode}} | |||
{{Box| 1= '''FREIWILLIG:''' |2 = Falls du noch Energie hast, kannst du hiermit nochmal das Multiplizieren von Dezimalbrüchen üben...nimm dir bitte für Nebenrechnungen einen Stift und dein Heft zur Hand, das Erraten der Lösungen bringt leider nicht sehr viel... <br> {{LearningApp|app=3095700|width=100%|height=700px}} | |||
|3 = Arbeitsmethode}} | |||
Aktuelle Version vom 29. Januar 2021, 18:58 Uhr
25.01.2021
27.01.2021: Multiplizieren von Dezimalbrüchen
28.01.2021: Multiplizieren von Dezimalbrüchen