M5 V Flächeninhalt: Unterschied zwischen den Versionen
Aus RMG-Wiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<[[5b 2019 20]] | <[[5b 2019 20]] | ||
==1 Flächenvergleich== | ===1 Flächenvergleich=== | ||
{{Box|Merke| | {{Box|Merke| | ||
Zerlegt man eine Fläche so, dass sie mit einer anderen Fläche übereinstimmt, so haben die beiden Flächen denselben Flächeninhalt. | Zerlegt man eine Fläche so, dass sie mit einer anderen Fläche übereinstimmt, so haben die beiden Flächen denselben Flächeninhalt. | ||
| Zeile 10: | Zeile 10: | ||
|3=Üben}} | |3=Üben}} | ||
==2 Einheiten für Flächeninhalte== | ===2 Einheiten für Flächeninhalte=== | ||
{{Box| | {{Box|1=Üben|2= | ||
Vorsicht! Hier stehen verschiedene Einheiten. Gib in der in Klammern angegebenen Einheit an. Notiere in dein Heft | Vorsicht! Hier stehen verschiedene Einheiten. Gib in der in Klammern angegebenen Einheit an. Notiere in dein Heft. | ||
# 12 cm² (mm² | <div class="lueckentext-quiz"> | ||
# 2300 dm² (cm² | # 12 cm² = '''1200()'''mm² | ||
# 400 m² (cm² | # 2300 dm² = '''230000()'''cm² | ||
# 3,4 ha (a | # 400 m² ='''4000000()'''cm² | ||
# 340 a (ha | # 3,4 ha ='''340()'''a | ||
# 3,4 km (m | # 340 a ='''3,4()'''ha | ||
# 3,45 cm² (mm² | # 3,4 km ='''3400()'''m | ||
# 0,3 m² (dm² | # 3,45 cm² ='''345()'''mm² | ||
# 3dm 4mm (cm | # 0,3 m² ='''30()'''dm² | ||
# 1m² 34dm² (dm² | # 3dm 4mm ='''30,4()'''cm | ||
# 1m² 34dm² (m² | # 1m² 34dm² ='''134()'''dm² | ||
# 1m² 34dm² ='''1,34()'''m² | |||
</div> | |||
|3=Üben}} | |||
{{Box|Merke| | |||
Mit Hilfe der Einheitentabelle kannst Aufgaben wie die letzten beiden oben leicht bearbeiten. | |||
Lies dir auf Seite 227 die Information zur Einheitentabelle durch. | |||
|Merksatz}} | |||
{{Box| Übung zur Umwandlung bei gemischten Einheiten| | |||
Bei den Aufgaben steht im blauen Kästchen ein Beispiel, wie die Lösung in deinem Heft aussehen soll. | |||
* Bearbeite im Buch S.228/2a,c,i-k und 3a,c,e-g | |||
* Jetzt kommen Kommas hinzu. Wenn du dir unsicher bist, so lies oben auf Seite 228 die Information zur Kommaschreibweise durch. | |||
* Bearbeite S.228/5 a-h und 7 e-i | |||
|Üben}} | |Üben}} | ||
==Flächeninhalt und Umfang von Rechtecken== | |||
===Flächeninhalt und Umfang von Rechtecken=== | |||
{{Box|Kästchen zählen| | {{Box|Kästchen zählen| | ||
Ihr kennt bereits die verschiedenen geometrischen Figuren. | Ihr kennt bereits die verschiedenen geometrischen Figuren. | ||
| Zeile 37: | Zeile 52: | ||
|Üben}} | |Üben}} | ||
{{2Spalten| | |||
{{Box|Info| | {{Box|Info| | ||
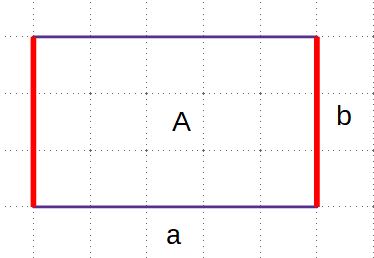
Bei einem Rechteck bezeichnet man die Seiten mit a und b. | Bei einem Rechteck bezeichnet man die Seiten mit a und b. | ||
|Unterrichtsidee}}| | |||
[[Datei:Rechteck02.jpg|midi]] | [[Datei:Rechteck02.jpg|midi]] | ||
}} | |||
{{Box|1 = Zeichnen von 3 Rechtecken|2= | {{Box|1 = Zeichnen von 3 Rechtecken|2= | ||
Ins Übungsheft: | |||
[[Datei:Einheitsquadrat.jpg|alternativtext=|rechts|100px]] | |||
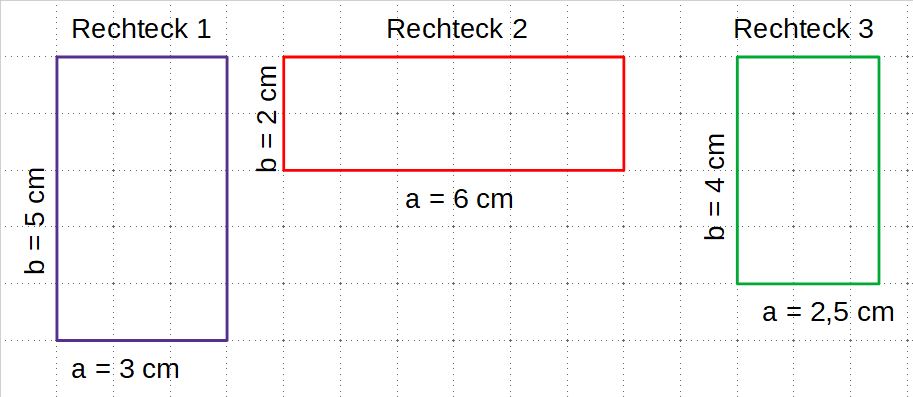
* Zeichne ein Rechteck mit den Maßen a = 3cm; b = 4cm, ein Rechteck mit den Maßen a= 2cm und b = 6cm und das dritte Rechteck hat die Seitenlängen a = 8cm und b = 1,5 cm. Notiere die Seitenlängen am Rechteck. | * Zeichne ein Rechteck mit den Maßen a = 3cm; b = 4cm, ein Rechteck mit den Maßen a= 2cm und b = 6cm und das dritte Rechteck hat die Seitenlängen a = 8cm und b = 1,5 cm. Notiere die Seitenlängen am Rechteck. | ||
* Aus wie vielen 1cm² bestehen die Rechtecke? (Zur Erinnerung: 1cm² hat die Maße 1cm x 1cm, also 4 Kästchen) | * Aus wie vielen 1cm² bestehen die Rechtecke? (Zur Erinnerung: 1cm² hat die Maße 1cm x 1cm, also 4 Kästchen) | ||
| Zeile 54: | Zeile 71: | ||
* Notiere, was dir auffällt. | * Notiere, was dir auffällt. | ||
|3 = Üben}} | |3 = Üben}} | ||
{{Navigation verstecken | {{Navigation verstecken | ||
|[[Datei:Rechtecke02.jpg|midi]] | |[[Datei:Rechtecke02.jpg|midi]] | ||
| Zeile 60: | Zeile 78: | ||
|Lösung ausblenden}} | |Lösung ausblenden}} | ||
{{2Spalten| | |||
{{Box|1=Info|2= | {{Box|1=Info|2= | ||
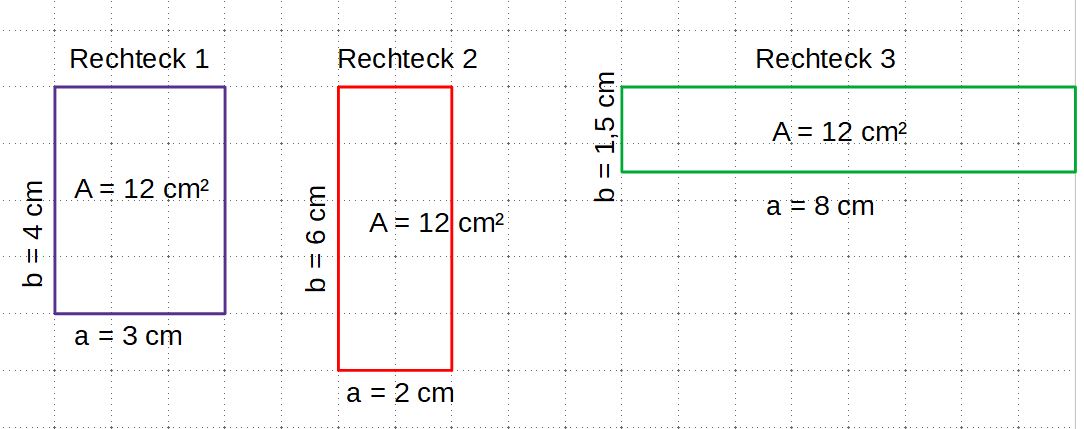
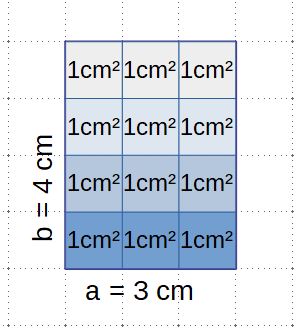
Möchte man den Flächeninhalt eines Rechtecks bestimmen, so kann man es erst einmal in gleich große Streifen zerlegen. | Möchte man den Flächeninhalt eines Rechtecks bestimmen, so kann man es erst einmal in gleich große Streifen zerlegen. | ||
Dieses Rechteck besteht aus 4 Streifen mit je 3 cm². | Dieses Rechteck besteht aus 4 Streifen mit je 3 cm². | ||
Der Flächeninhalt A dieses Rechtecks beträgt also: <math>A = 4 \cdot 3 cm^2 = 12 cm^2</math> | Der Flächeninhalt A dieses Rechtecks beträgt also: <math>A = 4 \cdot 3 cm^2 = 12 cm^2</math> | ||
|3=Unterrichtsidee}} | |3=Unterrichtsidee}}| | ||
[[Datei:Rechtech03.jpg|midi]]}} | |||
| Zeile 93: | Zeile 112: | ||
# Nachdem du die Kästchen gezählt hast, berechne nun auch den Flächeninhalt der anderen beiden Rechtecke Seitenlängen a = 8 cm und b = 1,5 cm sowie das Rechteck a = 2 cm und b = 6 cm, die du in dein Heft gezeichnet hast, mit Hilfe der Formel. ''Tipp:''Wandle bei Kommazahlen beide Seitenlängen in die nächstkleinere Einheit um und rechne dann. | # Nachdem du die Kästchen gezählt hast, berechne nun auch den Flächeninhalt der anderen beiden Rechtecke Seitenlängen a = 8 cm und b = 1,5 cm sowie das Rechteck a = 2 cm und b = 6 cm, die du in dein Heft gezeichnet hast, mit Hilfe der Formel. ''Tipp:''Wandle bei Kommazahlen beide Seitenlängen in die nächstkleinere Einheit um und rechne dann. | ||
# Berechne nun auch unter/neben den Rechtecken den Umfang. Was fällt dir auf? | # Berechne nun auch unter/neben den Rechtecken den Umfang. Was fällt dir auf? | ||
{{Lösung versteckt|Lösung: Der Flächeninhalt bei allen drei Rechtecken ist gleich. Aber der Umfang ist unterschiedlich.}} | {{Lösung versteckt|Lösung: Der Flächeninhalt bei allen drei Rechtecken ist gleich. Aber der Umfang ist unterschiedlich. <br> | ||
Rechteck 1: U = 2*4cm + 2*3cm = 14cm <br> | |||
Rechteck 2: U = 2*2cm + 2*6cm = 2cm + 12cm = 16 cm <br> | |||
Rechteck 3: U = 2*8cm + 2*1,5cm = 2*80mm + 2*15mm = 160mm + 30mm = 16cm + 3cm = 19 cm | |||
}} | |||
|3=Üben}} | |3=Üben}} | ||
| Zeile 108: | Zeile 131: | ||
c) a = 5 dm, b = 12 dm | c) a = 5 dm, b = 12 dm | ||
A='''60()'''dm²; U = ''' | A='''60()'''dm²; U = '''34dm()''' | ||
d) a = 23 m, b = 8 m | d) a = 23 m, b = 8 m | ||
| Zeile 116: | Zeile 139: | ||
{{Lösung versteckt|1= a) A=4cm*7cm= 28cm²; U = 2*4cm + 2*7cm = 22cm <br> | {{Lösung versteckt|1= a) A=4cm*7cm= 28cm²; U = 2*4cm + 2*7cm = 22cm <br> | ||
b) A = 4mm*7mm = 28 mm²; U = 2*4mm + 2*7mm = 22mm <br> | b) A = 4mm*7mm = 28 mm²; U = 2*4mm + 2*7mm = 22mm <br> | ||
c) A = 5dm*12dm = 60 dm²; U = 2*5dm + 2*12dm = | c) A = 5dm*12dm = 60 dm²; U = 2*5dm + 2*12dm = 34dm <br> | ||
d) A = 23m*8m = 184 m²; U = 2*23m + 2*8m = 46m + 16m = 62m }} | d) A = 23m*8m = 184 m²; U = 2*23m + 2*8m = 46m + 16m = 62m }} | ||
Aktuelle Version vom 19. Juli 2020, 09:46 Uhr
1 Flächenvergleich
2 Einheiten für Flächeninhalte
Flächeninhalt und Umfang von Rechtecken
a) A=4cm*7cm= 28cm²; U = 2*4cm + 2*7cm = 22cm
b) A = 4mm*7mm = 28 mm²; U = 2*4mm + 2*7mm = 22mm
c) A = 5dm*12dm = 60 dm²; U = 2*5dm + 2*12dm = 34dm
Falls ihr mit anderen Einheiten gerechnet habt, dann vergleicht die Lösungen am Ende. Dort sind sie in verschiedenen Einheiten angegeben.
a) A= 5cm*70dm= 5cm*7cm= 35cm² = 3500dm²
b) A = 1200mm*9dm = 12dm*9dm = 108dm² = 10800cm² = 1080000mm²
c) A = 5km*3000m = 5km*3km = 15 km² = 1500 ha = 150 000a = 15 000 000 m²
d) A = 50cm*200mm = 50cm*20cm = 1000 cm² = 100 000mm² = 10 dm²
e) A = 1200dm*15m = 120m*15m = 1800 m² = 18 000 000cm² oder gleich in cm umrechnen: 12000cm*1500cm